
Promjenljivost rente
SEMINARSKI RAD IZ PREDMETA:
FINANSIJSKA I AKTUARSKA MATEMATIKA
TEMA: PROMJENLJIVOST RENTE
SADRŽAJ:
UVOD.............................................................................................................3
1. VARIJABILNE RENTE...........................................................................4
2. RENTE SE MIJENJAJU PO ZAKONITOSTIMA
ARITMETIČKE PROGRESIJE.................................................................4
2.1. Dekurzivne rente....................................................................................5
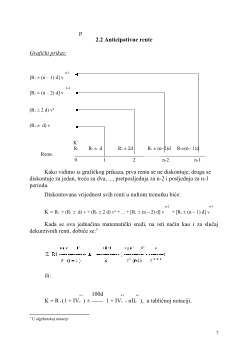
2.2. Anticipativne rente.................................................................................7
2.3. Primjeri................................................................................................... 8
3. RENTE SE MIJENJAJU PO ZAKONITOSTIMA
GEOMETRIJSKE PROGRESIJE..............................................................9
3.1. Dekurzivne rente....................................................................................9
3.2. Anticipativne rente.................................................................................11
3.3. Primjeri................................................................................................... 12
ZAKLJUČAK................................................................................................13
LITERATURA.............................................................................................. 14
2
1. VARIJABILNE RENTE
Ako se iznosi rente mijenjaju po nekom matematskom zakonu, onda se
takvi iznosi mogu posmatarati kao varijabilne rente.
U ovom radu će se proučavati samo rente koje se mijenjaju po
zakonitostima aritmetičke i geometrijske progresije.
Varijabilnost rente se može posmatrati sukcesivno i u serijama.
Period isplate kod varijabilnih renti može biti jednak, manji i veći od
perioda kapitalisanja.
2. RENTE SE MIJENJAJU PO ZAKONITOSTIMA ARITMETIČKE
PROGRESIJE
Ako je svaka sljedeća renta veća, odnosno manja od prethodne za
konstantan iznos, koji se označava sa
d
, onda se govori o rentama koje se
mijenjaju po zakonitostima aritmetičke progresije.
Za slučaj kada rente opadaju po aritmetičkoj progresiji mora biti
zadovoljen uslov da je:
(n – 1) d < R
1
,
gdje je:
n – broj perioda
R – renta
Krčmar, M.:
Finansijska matematika i metode nvesticionog odlučivanja
, Kemigrafika, Sarajevo, 2002.,
Krčmar, M.:
Finansijska matematika i metode nvesticionog odlučivanja
, Kemigrafika, Sarajevo, 2002.,
4
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































