
Pouzdanost u inžinjerstvu
1
1. SISTEMI U MAŠINSTVU I USLOVI RADA
1.1 SISTEMI U MAŠINSTVU
Sistem u mašinstvu predstavlja skup elemenata, relacija i njihovih karakteristika povezanih međusobno u
celinu, na način pogodan za vršenje korisnog rada. Pojam sistem je izveden iz grčke reči “
” koji
označava celinu sastavljenu iz delova.
Element je sastavni deo neke celine. Prema rečniku EOQC, element se definiše kao : deo, sklop, podsistem ili
sistem koji može biti podjednako razmatran ili odvojeno ispitivan ili testiran. Ovo znači, da za funkcionisanje
sistema nije dovoljan samo kvalitet elemenata u celini, već i potpuna određenost relacija između njih.
Danas imamo sisteme u mašinstvu, energetske, obrazovne, sisteme centralnog grejanja, telekomunikacione
sisteme, sisteme naoružanja i odbrane, društvene sisteme, ekonomske sisteme i sl. Sistemi različitih vrsta su
rezultat procesa projektovanja, dok je vrednovanje sistema problem sistem-analize.
Sistemski prilaz omogućuje određivanje sistema u f-ciji posmatrača.
Primeri sistema:
Sistem je čovek (bio-sistem), sistem je i mašina.
Sistem je čovek-mašina-alat-obradak-režimi rada
obradni sistem.
Sa aspekta funkcije izlaza, osnovna hijerarhija sistema može se strukturno prikazati na sl.1 ili u obliku:
ili dalje:
Sistemi u mašinstvu su najrazličitije vrste:
ENERGETSKI, TRANSPORTNI, PROIZVODNI,
OBRADNI
i
razni drugi, u zavisnosti od postavljene funkcije cilja i uslova okoline. U suštini, to su sve RADNI SISTEMI,
koji pretvaraju ulazne veličine u izlazne, u skladu sa potrebama vršenja određenog rada.
1.2 MODEL FUNKCIONISANJA TEHNIČKIH SISTEMA
Sam rad sistema je veoma dinamičan, i stoga, imajući to u vidu, dolazimo do nekoliko zaključaka:
.….
.….
.….
(S)
SISTEM
PS
1
PS
2
PS
j
PS
n
E
11
E
1
r
.….
E
n
1
E
nr
sl.1 Osnovna struktura sistema
2
*
f-cija kriterijuma
je određena željenim ciljem od strane donosioca odluke;
* sistem pretvara ulazne
u izlazne veličine
, na
bazi date f-cije kriterijuma
i projektovanih
postrupaka rada;
* sistem funkcioniše u okolini, čije je dejstvo
promenljivog karaktera
(otvorenost, dinamičnost), što
izaziva poremećaje u procesima rada,
* u rezultatu poremećaja, javljaju se gubici koji umanjuju efekte i izvode sistem izvan granica
odstupanja,
* rad sistema izvan granica dozvoljenih odstupanja izaziva potrebu
REGULISANJA
(upravljivost), tj.
postupak koji traži obrađene informacije o sistemu, moguće je sistem predstaviti na sl.3.
1.3 OSNOVNI PROCES TRANSFORMACIJE ( ulazi, izlazi, gubici...)
U osnovi, mašinski sistemi su radni sistemi koji pretvaraju ulazne veličine u izlazne, u skladu sa potrebama
vršenja određenog rada. Ulazne veličine su po pravilu materijalne i nematerijalne prirode, a isto važi i za izlazne
veličine.
Kod sistema u mašinstvu ulazi su:
MATERIJAL,
ENERGIJA,
INFORMACIJE,
RAD,
NOVAC,
VREME,
I
i
z
2
z
1
z
.
.
.
}
{
X
p
y
SISTEM
(procesi rada)
………
.
.
.
n
x
2
x
1
x
ulaz
sl.2 Model funkcionisanja tehničkih sistema
korekcije
}
{
Y
S
j
d
odluka
Obrada
podataka
1
y
izlaz
………
}
{
Z
Funkcija
kriterijuma
ponori

4
upravljivosti), uslovljavaju izgradnju sistema u mašinstvu i intenzivniji režim rada i veći stepen tačnosti, što u
suštini vodi usložnjavanju struktura ove vrste sistema (tehnički sistemi).
Usložnjavanje strukture u radnom, mernom i upravljačkom delu od osnovnih do složenih, je karakteristika
daljeg razvoja svih tehničkih sistema (sl.4).
Na sl.4 je dat prikaz jednopozicionog (osnovna struktura) i višepozicionog (složena struktura) obradnog
sistema, i iz ovog proizilazi da f-cija kriterijuma, u smislu povećanja efektivnosti-učinka uz isti kvalitet, dovodi
do:
-
usložnjavanja strukture sistema; i
-
povećanja stepena automatizacije.
Prethodna razmatranja potvrđuju da složenost na relaciji SISTEM-OKOLINA raste i da je sve teže zadovoljiti
uslove rasta.
1.6 OSNOVNA STANJA SISTEMA
Složenost strukture sistema i projektovanih odnosa između elemenata sistema u vršenju sve složenijih f-cija
kriterijuma, povećavaju entropiju sistema, čineći ih potencijalno podložnijim otkazima u vršenju f-cije i
POTREBA AUTOMATIZACIJE
SISTEM
Slika4: Usložnjavanje strukture sistema
sl.5 Odnos karakteristika sistema
K
ar
ak
te
ri
st
ik
a
si
st
em
a
t
k
Kr
Ku
vreme
Ku - nivo ugrađenih
karakterustika
Kr - nivo radnih
karakteristika sistema
5
istovremeno prouzrokujući prekide i zastoje u radu. Ilustracije radi, samo iz jednostavnije strukture izneti stav
se evidentno može ilustrovati (sl.6).
sl.6 Dinamika osnovnih stanja sistema
Kao što se vidi, procesu rada sistema u mašinstvu odgovaraju dva osnovna stanja:
-
stanje sistema u RADU i
-
stanje sistema u OTKAZU
Otkaz elemenata izaziva otkaz sistema ili traži uvođenje paralelnih veza, što sve umanjuje ukupne izlazne
veličine sistema (sl.6). Ilustracije radi na sl.6 data je dinamika - slika stanja sistema.
U rezultatu se na kraju perioda T može konstatovati da se sistem nalazio:
u
RADU
:
u vremenu
i
u
OTKAZU:
u vremenu
;
pri čemu je
;
Razvoj
sistema u mašinstvu (tehničkih) je uslovljen postojanjem vremenske slike ponašanja sistema,
koja omogućuje utvrđivanje stanja u smislu:
Te
or
ij
sk
a
vr
ed
no
st
iz
la
za
St
va
rn
a
vr
ed
no
st
iz
la
zn
e
ve
lič
in
e
0
Iz
la
zn
a
ve
li
či
na
si
st
em
a
uo
uo
t
T
ur
ur
t
T
1
uo
t
i
ur
t
3
ur
t
2
ur
t
1
ur
t
2
uo
t
j
uo
t
sl.7 Stanje sistema
2
S
E
23
t
u radu
ELEMENAT 1
vreme t
SISTEM
ELEMENAT 2
n
S
E
4
S
E
3
S
E
2
S
E
1
S
E
0
S
E
1
S
E
vreme t
u otkazu
n
t
2
22
t
21
t
n
t
2
13
t
12
t
11
t
7
Egzaktan pristup ovom problemu, bazira se na
teoriji pouzdanosti,
kao naučnoj disciplini koja se bavi
proučavanjem zakonitosti kojih se treba pridržavati pri projektovanju, konstruisanju, ispitivanju, proizvodnji i
eksploataciji tehničkih proizvoda, kako bi oni imali što duži vek, a time i maksimalni radni učinak.
Istorijski gledano, razvoj teorije pouzdanosti je kratak.
Smatra se da su prva ispitivanja pouzdanosti počela prikupljanjem podataka o otkazima agregata u avionima
tridesetih godina prošlog veka. Početkom 40-tih godina utvrđuje se propis da avioni mogu imati najviše 1 otkaz
na 100.000 sati leta, s obzirom na visok stepen opasnosti takvog otkaza.
Gledano hronološki, teorija pouzdanosti najpre se razvila četrdesetih godina dvadesetog veka u SAD i u
Sovjetskom Savezu ( danas Rusija), pedesetih godina dvadesetog veka, uglavnom za potrebe 20-tog veka.
Rečenica koja je pronađena na glinenoj pločici u arhivama firme " Sinovi Murasu" iz Nippura u Indiji, koja
datira iz trideset pete godine vladavine Artaxeresa I, 429.godine pre nove ere, jasno govori o tome koliko je
pojam pouzdanosti star. Ta rečenica glasi glasi:
" Što se tiče zlatnog prstena sa smaragdom, mi garantujemo da sledećih dvadeset godina smaragd neće ispasti
iz zlatnog prstena. Ako bi smaragd ispao iz zlatnog prstena, pre nego što prođe 20 godina, mi ćemo isplatiti
Bel- Nadimu odštetu od deset mana u srebru
."
Neke od prisutnih definicija pouzdanosti:
Pouzdan je onaj sistem koji izvršava svoju funkciju bez kvara – otkaza.
Pouzdanost je verovatnoća, na određenom nivou poverenja, da će sistem uspešno obaviti funkciju za
koju je namenjen, bez otkaza i unutar specifikovanih granica performansi, uzimajući u obzir prethodno
vreme korištenja sistema, u toku specificiranog vremena trajanja zadatka.
“Pouzdanost je verovatnoća, na određenom nivou poverenja, da će sistem (mašina) uspešno obaviti
funkciju za koju je namenjen, bez otkaza i unutar specificiranih granica performansi, uzmajući u obzir
prethodno vreme korištenja sistema, u toku specificiranog vremena trajanja zadatka, kada se koristi na
propisani način i u svrhu za koju je namenjen, pod specificiranim nivoima opterećenja”.
“
Pouzdanost je verovatnoća da će sistem uspešno vršiti funkciju kriterijuma u projektovanom
vremenu rada i datim uslovima okoline.
” ( prema američkom MIL standardu)
" Pouzdanost se definiše kao svojstvo objekta da ispunjava zadate funkcije i održava vrednost
eksploatacionog parametra tokom vremena u zadatim granicama, koje su određene zadatim režimima i
uslovima korišćenja, tehničkog opsluživanja, remonta, skladištenja i transporta.
“Pouzdanost je sposobnost tehničkog sistema da izvršava zahtevanu funkciju, pod datim uslovima i u
datom intervalu vremena. ”
“Pouzdanost je sposobnost sredstva da izvršava zahtevane funkcije u određenim uslovima za određeni
period vremena.
Pouzdanost sredstava za rad je merilo o tome kako je često moguće očekivati kvar sredstva u određenim
uslovima eksploatacije.”
8
Pouzdanost se može definisati na više načina, a suština je da pouzdanost predstavlja verovatnoću da će sistem
uspešno obaviti zadatu funkciju, bez otkaza
.
U svim navedenim definicijama, prisutna su dva nezaobilazna faktora:
vreme rada
i
uslovi rada.
. Izraz
proizvod je apsolutno pouzdan,
se u situaciji kada se govori o određenim uslovima, zamenjuje
određenim
numeričkim kriterijuamima.
Stoga se podaci koji se daju za pouzdanost, odnose samo na vremenski
interval i specificirane uslove rada.
Vidi se da je pouzdanost verovatanoća, jer se iskazuje brojčano vrednostima između 0 i 1, ili vrednostima
između 0 % i 100 %.
Što se tiče ekonomske strane problema, mora se naglasiti da cena nepouzdanosti ne predsavlja samo cenu
proizvoda koji je otkazao, već uzima u obzir i prateće efekte koji su nastali zbog otkaza:
1. Troškovi održavanja,
2. Cena rezervnog dela,
3. Troškovi držanja dela na skladištu,
4. Troškovi transporta,
5. Izgubljeno vreme zbog nekorišćenja sistema usled otkaza nekog od elemenata u sistemu,
6. Psihološki efekti.
Zahtevi po pitanju pouzdanosti sve više rastu, tako da su danas u razvijenim zemljama razrađeni posebni propisi
kojima se preciziraju tehnički uslovi pouzdanosti odgovornih sistema.
Npr. NASA ima svoje specifične propise o pouzdanosti, koje moraju da zadovolje svi oni koji žele da postanu
dobavljač NASE.
2.2 ULOGA POJEDINIH FAZA ŽIVOTNOG CIKLUSA PROIZVODA NA POUZDANOST
PROIZVODA
O pouzdanosti se mora voditi računa još u fazi projektovanja i konstruisanja. Uslovi rada mašinskih sistema su
slučajnog karaktera, proces razaranja i druge vrste oštećenja su rezultat slučajnih procesa. Mašinski sistem
predstavlja materijalizovani proizvod ljudskog rada, koji ima mogućnost izvršenja određene funkcije. Proces
razvoja mašinskih sistema počinje idejom - zahtevom za novim proizvodom, a završava se izradom i
ispitivanjem. Nakon toga, proizvod započinje drugu etapu – period eksploatacije, u kome ono što će se dalje
dešavati sa njim zavisi od uslova eksploatacije i pridržavanje korisnika uputstava koja su data za rukovanje.
U dosta dugačkom vremenskom periodu problemi projektovanja i izgradnje sistema u mašinstvu su rešavani
prvenstveno sa stanovišta kinematike mehanizama, otpornosti materijala, potrebne snage i učinka. Zadatak
projektanata se svodio u prvom redu na obezbeđivanje mogućnost funkcionisanja. Kvalitet funkcionisanja u
vremenu i datim uslovima okoline skoro da nije bio predmet razmatranja. Sistem je zadovoljavao samo zahteve
nižega reda i u vremenu u kome je sistem imao nivo ugrađenih iznad nivoa radnih karakteristika. Međutim, nivo
radnih karakteristika raste u vremenu, pa bi i nivo ugrađenih karakteristika trebalo da raste.
Usložnjavanje strukture sistema, kvaliteti materijala, tačnost i kvaliteti obrade omogućavaju potreban rast. U
pogledu napredovanja performansi proizvoda, koje sa pak stalno istovremeno umanjuje usled tribo-mehaničkih
efekata: habanje, deformacije, zamor, …; što dovodi do čestih otkaza u određenom trenutku (tačka ).
Jedna od osnovnih faza u izradi tehničkog sistema kao novog proizvoda je projektovanje. Značaj projektovanja
može da se ilustruje slikom - polugom kvaliteta.

10
Sl. 10. Dijagram zavisnosti nastajanja grešaka (kriva a) i otkazivanja i otklanjanja grešaka (kriva b) od faza
životnog veka proizvoda
Nivo troškova usled grešaka na tehničkom sistemu zavisi u kojoj fazi životnog ciklusa proizvoda su iste
otkrivene.U cilju izbegavanja nepotrebnih troškova, potrebno je delovati najviše u fazi projektovanja, odnosno
potrebno je proširiti ga u smislu:
-
obezbeđenja podloga o ponašanju sistema u procesu rada u vremenu i datim uslovima u cilju
identifikacije pojava, uzroka i učestalosti otkaza i vremena njihovih trajanja, odnosno poimanja
fizičke suštine otkaza;
-
primena kvalitativnih i kvantitativnih metoda ispitivanja odnosa radnih karakteristika i izlaznih
veličina sistema.
Ugradnja elemenata u postupku projektovanja i izrade treba da obezbede:
-
stupanje u rad sistema i postizanje nivoa postavljene f-cije cilja, tj. zadatih parametara: snaga, obrtni
moment, prohodnost, tačnost, stabilnost, krutost, radni učinak;
-
rad sistema u granicama dozvoljenih, kontrolisanih i upravljivih parametara;
-
adaptivnost sistema u zadatim granicama odstupanja radnih parametara;
-
vraćanje sistema po pojavi otkaza u stanje rada u određenom projektovanom vremenu i granicama
radnih parametara;
-
visoku pouzdanost, bezbednost i ekološku zaštitu sredine.
Kvalitetno projektovanje i oblikovanje sistema treba da zadovolji:
-
vršenje f-cija kriterijuma;
-
adaptivnost, upravljivost i visoku pouzdanost sistema;
-
minimalne zastoje po frekvenciji i minimalno vreme korektvnih mera;
-
korektivnim akcijama vraćanje sistema u projektovano stanje;
-
bezbednost, ergonomičnost i ekološke parametre.
VAŽNE NAPOMENE:
11
1. Pouzdanost se utemeljuje u fazi projektovanja, u fazi izrade obezbeđuje a u procesu eksploatacije
realizuje,
2. U
procesu konstruisanja
, može se uticati na pouzdanost proizvoda: oblikovanjem mašinskih delova i
sklopova, izborom materijala, izborom sistema podmazivanja, izborom metode zaštite od nepovoljnih
spoljašnjih uticaja,
3. U
procesu izrade,
na pouzdanost se utiče: kvalitetom izrade, kontrolom proizvodnje, kvalitetom
montaže sklopova i delova, mogućnošću automatskog upravljanja tehnološkim procesom,
4. U toku procesa eksploatacije, pouzdanost proizvoda zavisi od: uslova eksploatacije, ostvarenja sistema
tehničkog opsluživanja i remonta, režima rada.
5. Pri određivanju pouzdanosti sistema kao njegove značajne komponente efikasnosti, značajni uticaj
imaju:
1. način struktuiranja sistema (redni, paralelni, kompleksni);
2. međusobna uslovljenost - odnosi komponenata u sistemu (relacije);
3. zavisnost izlaznih
od ulaznih
veličina i postupak transformacije.
Imajući u vidu da se ukupno vreme rada - trajnost tehničkih sistema najčešće meri u godinama i da su
investicioni troškovi ovih sistema visoki, to je analiza i određivanje parametara sa aspekta njegove
maksimizacije veoma bitna i značajna za investitora ili korisnika istog.
2.3
POJAM OTKAZA I KLASIFIKACIJA OTKAZA
2.3.1POJAM OTKAZA
Otkaz je događaj koji ima za posledicu gubitak radne sposobnosti.
Svaki otkaz nastupa posle izvesnog vremenskog perioda rada, kada bilo koji parametar rada dostigne
graničnu vrednost
.
Otkaz može nastupiti usled razaranja nekog mašinskog dela, prekida neke funkcionalne veze sistema i sl., ali
isto tako se smatra da je otkaz nastupio i prekoračenjem granice tečenja, smanjenjem stepena korisnog dejstva
ispod dozvoljene vrednosti i sl.
Sa gledišta teorije pouzdanosti i teorije verovatnoće, otkaz objekta predstavlja slučajan događaj.
2.3.2 KLASIFIKACIJA OTKAZA
Otkazi se mogu podeliti na osnovu većeg broja kriterijuma.
Otkazi se dele:
a.) Prema karakteru izmene karakterističnog parametra do momenta nastanka otkaza odnosno
prema brzini nastajanja na:
-
Iznenadne otkaze
-
Postepene otkaze
- U toku rada sistema njihovi elementi su izloženi postepenom slabljenju.
Ovo slabljenje se ogleda i u promeni određenih parametara, a neispravnost
nastupa u onom momentu kada jedan od parametara dostigne dozvoljenu granicu.

13
e.)
Prema načinu otklanjanja:
Postojani,
Otkazi koji se otklanjaju sami od sebe.
f.)
Prema načinu ispoljavanja
, odnosno mogućnosti detektovanja:
Očigledni,
Prikriveni
.
g.)
Prema uzroku nastanka
:
Konstrukcioni
– greške konstruktora ( netačna konstrukcija sklopova, pogrešno proračunate
čvrstoće, pogrešno odabrane tolerancije i naleganja, lose projektovana krutost…),
Tehnološki
– greške pri izradi ( pogrešno odabran materijal, nepravilna izrada…) i
Eksploatacioni
– nepravilno rukovanje ili vanredni uslovi eksploatacije.
h
.) Prema prirodi nastanka na
:
Prirodne i
Veštačke otkaze
.
i
.) Prema vremenu nastank
a na:
-
Otkaze u vreme uhodavanja mašine,
- Otkaze u periodu normalne eksploatacije,
- Otkazi pri kraju veka mašine.
j.)
Prema vremenu nastanka na:
Rane,
Kasne i
Pozne otkaze
.
2.3 OSNOVNI POJMOVI KOJI SE VEZUJU ZA POUZDANOST ( teorija pouzdanosti, objekat
pouzdanosti, otkaz, pokazatelji pouzdsanosti)
Pouzdanost je veoma složen pojam, i predstavlja jednu od najvažnijih karakteristika sistema.
Teorija pouzdanosti
je deo primenjene matematike, u kome se ispituju načini proračuna pouzdanosti sistema,
metode procene pouzdanosti gotovih proizvoda, i optimizacija i povećanje efikasnosti funkcionisanja složenih
tehničkih sistema i njihovih komponenti u procesu eksploatacije.
Da bismo odredili parametre pouzdanosti, potrebno je dobro poznavanje sistema i nekih osnovnih pojmova.
Objekat pouzdanosti
može da bude tehnički sistem ili njegovi elementi ( građevine, mašine, aparati, pribori,
agregati i njihovi delovi).
Kada su u pitanju mašinske konstrukcije, objekat pouzdanosti može da bude : mašinski deo, kinematski par,
mašinski sklop, agregat, mašina i grupa mašina.Međutim, ova podela je uslovna jer se jedan mašinski sklop
može smatrati sistemom, ali i elementom neke mašine. Zato se u teoriji pouzdanosti usvaja da
element
predstavlja objekat čija se pouzdanost proučava nezavisno od njegovih sastavnih delova, a da
sistem
predstavlja
objekat, čija se pouzdanost proučava, zavisno od njegovih sastavnih delova.
14
Pouzdanost bitno zavisi od stohastičkih procesa, tako da se odabir njenih pokazatelja vrši na osnovu
verovatnoće pojave nekog događaja.
Izbor pokazatelja pouzdanosti se vrši po diferencijalnoj i integralnoj semi, odnosno:
U diferencijalnoj šemi se prvo rešava kakva svojstva treba da imaju pokazatelji pouzdanosti, a potom
prema određenim normama se ustanovljavaju konkretni pokazatelji.
U integralnoj šemi, ustanovljava se spisak svih mogućih pokazatelja pouzdanosti, bez njihovog
razlikovanja po svojstvima.
Optimalno rešenje se dobija isključivanjem onih pokazatelja, koji nisu podložni normiranju, a prema
izabranim kriterijumima.
Za svaku šemu se formira mnoštvo alternativnih varijanti rešenja.
Ranije smo pomenuli koja su
dva osnovna stanja sistema
:
1. Sistem u radu i
2. sistem u otkazu.
Pod otkazom ili prestankom rada se podrazumeva prestanak sposobnosti sistema da obavlja svoju funkciju.
Otkaz je postepeni ili trenutni gubitak funkcionalne sposobnosti uređaja.
Otkaz jednog elementa sistema, ne mora da znači i otkaz celog sistema, ukoliko je njegova uloga u sistemu od
perifernog znančaja. Ali, ako je element od vitalnog značaja, onda je njegov otkaz i otkaz sistema.
Jedan od najznačajnih pokazatelja pouzdanosti je
učestanost otkaza
, koja se najčešće definiše kao očekivani
broj otkaza u određenom vremenskom intervalu.
Kriva raspodele učestanosti otkaza je “
kada
” kriva, i biće kasnije predstavljena.
U skladu sa krivom koja će biti predstavljena, jasno je da obično figurira visok broj otkaza inicijalno kada
mašina otpočinje svoj životni vek.
2.3.1 PARAMETRI FUNKCIONISANJA I RADNA ISPRAVNOST OBJEKTA
Parametri funkcionisanja
karakterišu različita svojstva objekta, kao što su npr: pokazatelji tačnosti
funkcionisanja, mehaničke karakteristike, kinematski i dinamički pokazatelji, ekonomski pokazatelji,
eksploatacioni pokazatelji itd.
Npr. eksploatacioni pokazatelji mogu biti: nosivost, snaga, vučno-brzinske karakteristike, proizvodnost,
parametri radnog procesa. Najčešće svaki objekat ima više parametara funkcionisanja, a njihove dopuštene
granične vrednosti su definisane normativnom dokumentacijom na osnovu tehničkih uslova, standarda i sl.
Radna ispravnost je stanje objekta pri kome je on sposoban da izvršava svoju zadatu funkciju, a da pri tojme
određeni parametric ne pređu granične vrednosti.

16
Slika 13 Stanje sistema
Vreme ispravnog rada do otkaza je slučajna veličina. Otkaz i vreme ispravnog rada, se mogu definisati
posmatranjem zavisnosti karakterističnog parametra funkcionisanja – f-je kriterijuma u f-ji vremena.
Za
obnovljive objekte
se može uzeti vreme ispravnog rada do prvog otkaza, od prvog do drugog, od drugog do
trećeg itd.
Kod
neobnovljivog
objekta, vreme ispravnog rada se odnosi isključivo na vremenski period od početka rada do
prvog otkaza, jer se kod takvih objekata ne obnavlja radna sposobnost.
Granično stanje objekta
je ono stanje pri kome dalju eksploataciju objekta treba prekinuti.
U praksi to stanje
obično nastupa kada je dalje ekonomski neopravdano vršiti popravke objekta. Za neobnovljive otkaze, granično
stanje nastupa sa nastajanjem prvog otkaza.
Radni vek
Tv
je vremenski period koji obuhvata celokupno vreme eksploatacije, ne uzimajući u obzir vreme
remonta objekta. Radni vek se definiše i kao vremenski period do nastajanja graničnog stanja objekta, s tim da
on uključuje samo vreme rada objekta, a ne vreme zastoja potrebno za remont objekta i vreme čekanja kada
objekat ne radi zbog nepotpunog iskorišćenja kapaciteta.
Efikasnost sistema
- ukupno vreme rada za sistem sa strukturom od samo dva elementa
i
može se
napisati u obliku:
gde su:
vremena bezotkaznog rada elemenata sistema (istovremenog).
Efektivnost sistema
predstavlja meru zadovoljenja postavljenih zahteva. Definiše se kao verovatnoća da će
sistem stupiti u dejstvo i potom raditi bez otkaza.
Praktično gledano, efektivnost sistema predstavlja meru zadovoljenja postavljenih zahteva, odnosno meru
stepena izvršenja zadate f-je cilja.
17
U praktičnom smislu, efektivnost sistema obuhvata tehnološko-upravljački proces vezan za određivanje,
merenje i kontrolu karakteristika sistema. Adekvatan prilaz i metodologija izučavanja efektivnosti i pouzdanosti
sistema u mašinstvu dat je na sl.14, koji obuhvata sledeće komponente:
1. G o t o v o s t
sistema - predstavlja verovatnoću da će sistem uspešno stupiti u dejstvo i ući u područje
dozvoljenih odstupanja postavljene f-cije kriterijuma u datom vremenu i datim uslovima okoline;
2. P o u z d a n o s t
sistema - presdstavlja verovatnoću da će sistem tokom višekratne upotrebe uspešno
vršiti f-ciju kriterijuma u projektovanom vremenu trajanja i datim uslovima okoline (motorno vozilo,
obradni, transportni, hidraulički, mehanički sistem), odnosno VEROVATNOĆU da će sistem
jednokratne upotrebe uspešno vršiti postavljani zadatak u datom vremenu i datim uslovima okoline;
3. F u n k c i o n a l n a p o d o b n o s t
sistema - predstavlja sposobnost sistema za uspešno
prilagođavanje uslovima okoline u projektovanom vremenu trajanja rada. Problem efikasnosti sistema je
trajni i permanentni kvalitativni parametar. Izučavanje sistema povišene efikasnosti, povišenih zahteva
(f-cije kriterijuma) i složenih struktura, sadrži osnovne veličine vezane za ponašanje sistema.
Za izračunavanje efektivnosti sistema, važi jednačina:
E (τ, t) = A(τ)
*
R(t)
*
FP ............................................................................................................. ( 4)
Gde su:
A (τ ) – raspoloživost sistema u ukupnom vremenu τ . Pod vremenom τ se podrazumeva kalendarsko vreme,
koje obuhvata vreme rada, vreme u otkazu i vreme skladištenja.
R ( t ) – pouzdanost sistema u vremenu rada t,
FP – funkcionalna podobnost predstavlja meru zadovoljenja zahtevanih performansi, odnosno stepen
prilagođavanja uslovima okoline.
EFEKTIVNOST SISTEMA
GOTOVOST
Verovatnoća da će sistem uspešno stupiti u
dejstvo u datom trenutku vremena i datim
uslovima okoline.
-pouzdanost
-ljudski faktor
-pogodnost održavanja
-podrška
POUZDANOST
Verovatnoća da će sistem uspešno vršiti
funkciju kriterijuma u projektovanom
vremenu i datim uslovima okoline.
FUNKCIONALNA PODOBNOST
Sposobnost sistema za uspešno prilagođavanje
uslovima okoline u projektovanom vremenu
rada
sl.14 Osnovni parametri efektivnosti sistema

19
Slika 15 Vreme otkaza i histogram učestanosti otkaza
Empirijska funkcija gustine otkaza se može prikazati jednačinom:
NAPOMENA:
Širina intervala Δt se određuje na osnovu izraza:
Δt=
.................................................................................................. (5)
Gde je t
min
– vreme pojave prvog otkaza,
t
max
- vreme pojave poslednjeg otkaza.
f(t) =
20
Apcisa se deli na vremenske intervale, a brojevi otkaza se sređuju po klasama. Brojevi otkaza u različitim
klasama predstavljaju se preko visine stubića.
Broj intervala se određuje na osnovu izraza:
z =
z = 1+3,3 log n
z = 5 log n
z = 2
............................................................................................................................................ (6)
Broj klasa treba pažljivo odabrati, da se ne pojavljuju prazni intervali, a ako se pojavi simetrična raspodela,
primenjuje se neparan broj intervala.
Ukoliko vrednost vremena otkaza padne na granicu između dva intervala, onda se on po pola ubraja u obe
granične klase.
CRTANJE HISTOGRAMA
:
Za vrednosti na ordinati histograma, može se uzeti:
apsolutna učestanost ----------------------------------- f
abs
= N ( Δt)
relativna učestanost ------------------------------------ f
rel
relativna učestanost procentualno izražena: --
-------- f
rel=
.....................
(7)
pri čemu je:
N ( Δt) – broj otkaza u intervalu Δt,
n – ukupan broj posmatranih elemenata u trenutku t=0.

22
2.4.3 KUMULATIVNA UČESTANOST POJAVE OTKAZA
Histogram kumulativne učestanosti se dobija na osnovu histograma učestanosti pojave otkaza, tako što se u
datom intervalu vremena i-te klase sabiraju relativne učestanosti do tekuće klase.
Slika 18 Kumulativna učestanost otkaza – histogram i empirijska funkcija kumulativne verovatnoće otkaza
F
m
=
............................................................................................ (8)
Kumulativna učestanost otkaza se može predstaviti kao f-ja vremena.
Ova funkcija se označava kao "empirijska"funkcija raspodele otkaza F (t).
NAPOMENA:
U nekom trenutku nije važno koliko će elemenata otkazati, već je naprotiv važno znati koliko je ukupno, do
određenog trenutka, delova otkazalo.
Empirijsksa funkcija kumulativne učestanosti pojave otkaza odnosno funkcija nepouzdanosti, određuje se
prema izrazu:
23
........................................................................................................................ (9)
Gde je N (t)- broj otkaza elemenata do trenutka t.
Kako veličina n ∞, broj klasa se povećava, širina intervala se smanjuje, a kontura histograma se
približava graničnom slučaju – glatkoj krivi f-je F (t).
Kada n ∞, dobija se funkcija raspodele otkaza F (t) kao integral funkcije gustine:
NAPOMENA:
Funkcije verovatnoća pojave određenih stanja sistema, mogu u opštem slučaju biti dvojake i to:
-
diskretne
-
ili f-cije prekidnih promena, kod kojih promenljive uzimaju konačan-određen broj
vrednosti;
-
kontinualne -
ili f-cije neprekidnih promena kod kojih promenljive uzimaju bilo koju vrednost u
okviru datog intervala
.
Kumulativna
f-cija gustine pojava stanja u otkazu sistema za slučaj kontinualnih promena oblika je:
ili granična vrednost f-cije gustine pojava stanja u otkazu po definiciji je:
Za slučaj prekidnih (diskretnih) promena kumulativna f-cija gustine pojava stanja u otkazu sistema je:
,
odnosno,
2.4.4 FUNKCIJA POUZDANOSTI I OSNOVNA JEDNAČINA POUZDANOSTI

25
(t)
- ukupan broj ispravnih elemenata u posmatranom trenutku
- ukupan broj elemenata u trenutku
.
VAŽNO:
Kumulativna f-cija R(t)
bezotkaznog rada sistema po svojoj definiciji predstavlja komponentu
pouzdanosti
u
Pri razmatranju KUMULATIVNE FUNKCIJE pojava stanja u radu od značaja je tip sistema. Sa tog aspekta
sistemi se mogu podeliti na:
1. sistemi koji ne podležu
postupcima održavanja
(opravki i zamena) u trenutku pojave stanja u
otkazu (zamena novim); i
2. sistemi koji podležu postupcima održavanja u trenutku pojave otkaza.
Funkcija gustine otkaza se obeležava sa
f
(
t
), a na osnovu osnovnih zakona iz teorije verovatnoće može se
napisati da je:
Diferenciranjem ove jednačine po vremenu dobija se:
pri čemu je:
............... ............ (16)
Sliks 20 Grafički prikaz osnovne jednačine pouzdanosti
Pri čemu je:
26
je f-cija gustine ili raspodele verovatnoća pojava stanja u radu.
Iz prethodnog sledi da je:
2.4.5 INTENZITET OTKAZA SISTEMA
Ako se pretpostavi da je neki objekat ispravno radio do nekog vremena t, onda je verovatnoća pojave otkaza u
sledećem vremenskom periodu Δt:
F ( t+Δt) – F (t)= [1- R(t+Δt)]- [1-R(t)] ........................................................................................... (18)
Intenzitet otkaza se definiše kao verovatnoća pojave otkaza u jedinici vremena, pod uslovom da se do
tada nije desio otkaz.
Intenzitet otkaza
predstavlja odnos gustine pojava stanja u otkazu i kumulativne gustine pojava stanja u radu.
Za slučaj
neprekidnih promena
stanja, intenzitet otkaza se dobija kao odnos:
. ..........................................
(19)
Intenzitet otkaza, kao i f-cija gustine pojava stanja u otkazu kao parametar f-cije efektivnosti od posebnog je
značaja za sisteme u mašinstvu.
Za
prekidne promene
stanja u tehničkim sistemima intenzitet otkaza se dobija na bazi istog prilaza, kao broja
ispravnih elemenata u vremenskom intervalu
i srednje vrednosti broja ispravnih elemenata u
istom intervalu, tj.:
....................................................................... (20)
gde je:
- broj elemenata sistema u radu.

28
I u ovom slučaju se uočavaju sva tri karakteristična perioda (sl.22). Zbog svog karakterističnog oblika ovaj
dijagram se ponekad naziva dijagram “k a d a”. Po9dsručja koja se iz6dvajaju su:
područje 1- rani otkazi,
područje 2 – slučajni otkazi i
područje 3 – pozni otkazi usled habanja i zamora.
Intenzitet otkaza se često naziva
stopom otkaza, brzina pojave otkaza (neispravnosti)
;
Kumulativna
f-cija intenziteta, stanja u otkazu se dobija po sličnom postupku kao i ostale kumulativne
funkcije, tako je na sl. 20:
........................................................................................................ (22)
ili diferenciranjem ovog izraza sledi:
;
kako je:
,
to je:
.
što daje integraljenjem:
,
odnosno:
Izraz
pokazuje da kumulativna funkcija intenziteta otkaza teži beskonačnosti
, kada
.
Diferenciranjem:
,
Kako je leva strana (A) jednaka
, to je :
)
29
3.0 STATISTIČKI POKAZATELJI
Sve slučajne veličine karakterišu određeni statistički pokazatelji.
Statistički pokazatelji su:
1. Srednja vrednost – m,
2. Mediana - M
e
3. Mod - M
o
4. Varijansa – σ
2
5. Standardna devijacija – σ
3.1 Srednja vrednost-
– MTTF- Mean Time to Failure
Srednja vrednost populacije
m
ili srednje vreme ispravnog rada, čija je gustina raspodele f(t) – kontinuirani
ili prekidni tok f-je raspodele)
Slika 23 Funkcija gustine

31
Vrednost slučajno promenljive veličine t, koja odgovara najvećoj verovatnoći njene realizacije, bez obzira
da li se menja kontinualno ili diskretno, naziva se
mod.
Za kontinuirano raspoređenu slučajnu veličinu, čija je gustina f(t), vrednost se određuje iz izraza:
…………………………………………………………………………………….. (27)
Kod diskretnih vrednosti slučajno promenljivih, mod je slučajna promenljiva sa najvećom verovatnoćom
realizacije događaja.
3.4 MERA RASIPANJA RASPODELE
Ukoliko se za jednu određenu populaciju, pored srednje vrednosti, odredi i mera rasipanja nezavisno
promenljive oko srednje vrednosti, njene osobine se prepoznaju sa mnogo više sigurnosti.
Mera rasipanja se naziva VARIJANSA.
Za kvantitativne promene, varijansa se izražava u obliku:
– m
2
……………………………………… (28)
odnosno, za diskretne promene:
-m)
2
·f(t
i
) =
·f(t
i
) –m
2
…………………………………………………………. (29)
Kvadratni koren iz varijanse je standardno odstupanje ( pozitivna vrednost).
σ=
…………………………………………………………………………………………………… (30)
Koeficijent varijacije "V" se definiše kao količnik standardne devijacije i srednje vrednosti:
………………………………………………………………………………………………. (31)
3.5 KARAKTERISTIČNE VELIČINE EMPIRIJSKE RASPODELE
32
Empirijska srednja vrednost
se određuje kao aritmetička srednja vrednost
m
. Za poznata vremena
ispravnog rada do otkaza t
1,
t
2
, ....t
n,
empirijska
srednja vrednost se određuje izrazom:
m=
…………………………………
……………………………….. (32)
Empirijska mediana
t
50
kod uzoraka kod kojih postoji niz konkretnih vrednosti posmatrane veličine t,
medijanu predstavlja vrednost koja se nalazi u sredini svih rezultata složenih u rastućem nizu:
t
50
………………………………………………………………………………
(33)
Empirijska varijansa se izražava u obliku:
S
2=
2
…………………………………………………………………......... (34)
Empirijska standardna devijacija se dobija neposredno iz empirijske varijanse u obliku:
S=
=
……………………………………………………………………………… (35)
Empirijski koeficient varijacije:
V= ……………………………………………………………………………. (36)
3.6 GRANICE POVERENJA
Kada se za neki odgovarajući uzorak izračuna srednja vrednost, sasvim je sigurno da ova vrednost neće biti
ista za celu populaciju.
Ukoliko se uzorak proširi, dobiće se verovatno neka druga vrednost, bliža prvoj vrednosti.
Ovo ukazuje na činjenicu da svaka srednja vrednost, određena na jednom ograničenom uzorku, nosi u sebi
odgovarajuću grešku, odnosno odstupa od stvarne vrednosti.
Stepen odstupanja zavisi od veličine uzorka i od zakona raspodele posmatrane slučajne veličine.
Ocena odstupanja izračunate srednje vrednosti od prave srednje vrednosti odgovarajuće raspodele, vrši se na
osnovu utvrđivanja granica, odnosno intervala poverenja.

34
f
i
……………………………………………………………………………………………………………………………….
(40)
gde je: n
i
– broj rezultata u i-toj klasi,
n – ukupan broj rezultata.
Na osnovu relativnih frekvencija dobijaju se kumulativne vrednosti.
Slika 26 Histogram, stepenasti dijagram i poligon
4. 0 VEROVATNOĆA ( POJAM, VRSTE)
4.1 DEFINISANJE POJMA VEROVATNOĆA
Osnovni pojam u teoriji verovatnoće je događaj.
Pod pojmom događaj se u svakom eksperimentu podrazumeva svaka činjenica koja može da proizađe ili ne
iz tog eksperimenta.
Da bi se omogućilo da se događaji upoređuju po stepenu mogućnosti da se dogode, neophodno je da se sa
takvim događajem poveže određeni broj, koji je utoliko veći ukoliko je veća mogućnost njegovog nastanka.
Da bi to bilo moguće, uvedena je jedinica merenja:
verovatnoća izvesnog događaja, tj. događaja koji će
sigurno proizići.
Za verovatnoću takvog događaja usvojen je broj 1, a svi ostali događaji koji su mogući, ali ne i izvesni,
imaju manju verovatnoću manju od 1.
Događaju koji u datom eksperimentu uopšte ne može da se dogodi, dodeljena je verovatnoća 0.
Izračunavanje verovatnoće slučajnog događaja se bazira na zakonu velikih brojeva, prema kome se, pri
neograničenom povećavanju broja ogleda, može sa praktičnom sigurnošću tvrditi da se učestanost događaja
malo razlikuje od njegove verovatnoće pojavljivanja u jednom ogledu.
DEF. 1
:
35
Pod verovatnoćom događaja A podrazumeva se odnos brojeva m(A) i n
.
P (A) =
............................................................................................................................................ (41)
Pri čemu je:
m(A) – broj elementarnih događaja koji predstavljaju realizaciju događaja A,
n – ukupan broj mogućih događaja.
Ukoliko ni jedan elementarni događaj ne realizuje događaj A, tada je m(A) =0, pa je P(A)=0.
PRIMER 1:
Ako postoji skup od 3 ispravna i 2 neispravna proizvoda proizvoda i iz tog skupa se uzme slučajno
3 proizvoda, kolika je verovatnoća da se među ta tri broja nađu dva ispravna i jedan neispravni
proizvod?
4.2 SUPROTNA VEROVATNOĆA
Neka se sa P(A) označi verovatnoća događaja A.
Kolika je verovatnoća da se ne odigra događaj A?
Matematički se to može zapisati:
P( ) = 1- P(A)
P( ) = 1-
=
…………………………………………………………………………… (42)
Može se uvesti oznaka da je:
Q(A) = P ( ),
Pa je : Q(A) + P(A) =1 ………………………………………………………………………. (43)
PRIMER 2:
Skup se sastoji od 7 ispravnih i 5 neispravnih proizvoda. Ako se iz tog uzorka odjednom uzme 3 proizvoda,
kolika je verovatnoća da će bar jedan od njih biti ispravan?
4.3 SABIRANJE VEROVATNOĆA

37
Tada, za istovremeno pojavljivanje događaja A
1,
A
2......
A
k,
uvodi se nova
oznaka :
A
1
A
2
...........
A
k
i znak " " se čita "
i
".
Prikaz ogađaja koji se ne isključuju:
Slika 28
DEFINICIJA 3:
Za dva događaja A
1
i A
2
se kaže da su nazavisna ako važi relacija:
P (A
1
A
2
...........
A
k) =
P ( A
1
) P(A
2
) ....
……………………………………………..
(46)
NAPOMENA:
Ukoliko se događaji međusobno isključuju, znači oznakom A
1 +
A
2
odgovara realizacija ilidogađaja 1 ili
2.
Ili jedan ili drugi!
P ( A
1
+ A
2
) =P(A
1
)+P(A
2
) …………………………………………………
(47)
Međutim, ako se događaji ne isključuju, onda može nastupiti ili A1, ili A2, ili oba, pa važi pravilo:
P ( A
1
A
2
) = P (A
1
) +P (A
2
) – P(A
1
A
2
) = P (A
1
) +P (A
2
) – P(A
1
) P(A
2
)
……………… (48)
4.5 VEROVATNOĆA SLOŽENIH DOGAĐAJA
38
Neka su A
1
i A
2
događaji definisani
u istom prostoru i neka im pripadaju verovatnoće P ( A
1
) i P ( A
2
).
Ako se ti događaji međusobno isključuju, oznaka + daje značenje događaja koji nastaje ako nastaje
događaj A
1
ili događaj A
2.
Oznaka "
+ "
se čita kao " ili " sa eksluzivnim značenjem:
i l i j e d a n i l i d r u g i
!
5.0 MATEMATIČKI MODELI ZAKONA RASPODELE OTKAZA
U analizi pouzdanosti tehničkih sistema, jedan od krajnjih ciljeva je utvrđivanje teorijskog zakona raspodele
slučajne veličine, vremena ispravnog rada do otkaza elemenata/sistema.
Preciznije rečeno, treba ustanoviti koji od poznatijih teorijskih zakona raspodele najviše odgovara empirijskim
podacima, tj. kojim zakonom raspodele se najviše mogu interpretirati rezultati koji su dobijeni empirijski.Tada
se, sa velikom verovatnoćom, mogu izračunati sve potrebne karakteristike posmatrane slučajno promenljive
veličine, mogu se vršiti svi potrebni proračuni i tako objektivnije odlučivati.
Treba istaći, da se u poslednje vreme, u istraživanjima efektivnosti, a posebno pouzdanosti, sve više koristi
Vejbulov zakon. Ovo neposredno sledi iz osobina ovog, parametarski definisanog, zakona raspodele, koji je
veoma elastičan i koji se može primeniti za široki opseg načina promena slučajnih veličina.

40
…………………………………………………………………. (50)
Na slici dole je dat izgled dijagrama binomne raspodele.
Slika 29 Binomna raspodela
U ovom primeru zahtev će biti zadovoljen ne samo kada je broj ispravnih sijalica jednak x, već i kada je
njihov broj veći od x. Prema tome, interesantna je verovatnoća funkcionisanja x, x + 1, . . . , n sijalica
.
Znači:
------------------------------------ (51)
Jednačina (2) može se napisati i u obliku:
------------------------------------------------ (52)
Funkcija oblika P( X ≤ x − 1) predstavlja kumulativnu funkciju raspodele.
41
U navedenom primeru, ako sa
y
obeležimo broj neispravnih sijalica, onda je uslov da ima
x − 1
ili manje
ispravnih sijalica isto što i uslov da ima y ili više neispravnih sijalica, tj.:
----------------------------------------------------------------- (53)
Slučajna promenljiva veličina Y koja predstavlja broj neispravnih sijalica, imaće analogno jednačini (1)
sledeću funkciju gustine verovatnoće:
------------------------------------------------------------ (54)
Ako se uvede oznaka
1− p = q
onda je:
---------------------------- (55)
Sada se jednačina (3) može pisati u sledećem obliku:
------------------ (56)
odnosno:
------------------ (57)
Srednja vrednost funkcije gustine verovatnoće date jednačinom biće:
------------------------------------ (58)
a predstavlja očekivani broj elemenata koji će uspešno obaviti neki zadatak, ako je
n
ukupan broj
elemenata, a
p
verovatnoća da će jedan sistem uspešno obaviti zadatak.
Srednja vrednost funkcije gustine verovatnoće date jednačinom (5) biće:

43
- empirijske (merene frekvencije) učestanosti pojava
- broj intervala vremena merenja.
Slika 30 Poasonova raspodela
5.2 RASPODELE NEPREKIDNOG KARAKTERA
U
slučaju neprekidnih raspodela slučajne veličine, raspodele koje se najčešće primenjuju su:
o
Normalna ( Gausova),
o
Eksponencijalna raspodela,
o
Logaritamsko normalna,
o
Relejeva raspodela ( u skripti),
o
Linearna raspodela,
o
Vejbulova raspodela.
5.2.1 NORMALNA RASPODELA
Normalna ( Gausova ) raspodela se primenjuje u statističkoj matematici veoma često, znatno više nego
ostale.
44
Njena primena je dosta izražena kod proračuna elemenata kod kojih dolazi do slabljenja materijala i za
predviđanje pouzdanosti sistema.
Karakteristika normalne raspodele je da je f-ja gustine otkaza kriva u obliku zvona, simetrična oko srednje
vrednosti.
Jednačina ove f-je glasi:
f(t)=
.......................................................................................................... ( 63)
Pri čemu je:
– srednja vrednost ( negde u literaturi m, μ, pa čak i u vašoj skripti),
σ
– standardna devijacija
t
- vreme do otkaza, broj obavljenih ciklusa do otkaza…
Normalna raspodela je
dvoparametarska raspodela
sa parametrima:
m
–
parametar položaja
i
σ
– parametar oblika,
Normalna raspodela predstavlja dobar model u slučajevima kada dolazi do postepenog starenja sistema
( habanja).
S obzirom da je f-ja gustine
simetrična kriva
, to se
poklapaju srednja vrednost, medijana i mod.
m
……………………………………………………………………………….. (64)
Funkcija verovatnoće otkaza ima oblik
:
F (t)
.................................................................................................... (65)
Funkcija pouzdanosti
R(t) je:
R(t) 1- F(t)
. dt .................................................................................................. (66)
Funkcija intenziteta otkaza:
...................................................................................................... (67)

46
Slika 33
Pri određivanju pouzdanosti retko se koristi oblik normalne raspodele dat jednačinom (4.18), jer se integral
te jednačine ne može izračunati u konačnoj formi.
Zbog toga se koristi tzv. standardizovana normalna raspodela ϕ ( z), za koju postoje tabele iz kojih se mogu
naći površine ispod funkcije gustine otkaza za bilo koju normalnu raspodelu.
Jednačina (4.18) može se prevesti u standardizovani oblik uvođenjem smene:
47
............................................................................... (68)
Pri čemu z predstavlja standardizovanu normalnu raspodelu.
Pošto površine ispod f( t) i φ ( z) moraju biti jednake uvodi se smena:
......................................................................................... (69)
Iz jednačine sledi:
............................................................................................ (70)
dok se diferenciranjem jednačine
dobija:
........................................................................................................... (71)
Zamenom u jednačinu
dobija se:
.......................................................................................... (72)
Uzimajuć i u obzir jednačinu (5) može se napisati konačan oblik standardizovane normalne raspodele:
................................................................. (73)
gde je z dato jednačinom (5).
Funkcija kumulativne raspodele biće jednaka:

49
........................................................................... (76)
Funkcija intenziteta otkaza λ(t)
dobija se iz jednačina:
.............................................................................. (77)
To je monotono rastuća funkcija vremena, a njen izgled je dat na slici 35.
Slika 35 Funkcija intenziteta otkaza u slučaju normalne raspodele
Posle određenog vremena se dobija da je:
T
sr
m
To jest, vreme bezotkaznog rada jednako je srednjoj vrednosti m.
Ovde treba dati napomenu koja se odnosi na površinu ispod funkcije f( t ) tj. φ( z).
Ove funkcije su definisane za vrednosti t, tj. z, od −∞ do +∞ , i onda je površina ispod nje jednaka 1.
Međutim, kako vreme ne može da bude negativno, u teoriji pouzdanosti se normalna raspodela definiše za
vrednosti t od 0 do +∞ .
50
To je sasvim prihvatljivo, jer na primer, kada je t = m − 4,5 σ = 0, tj. z = − 4,5 (slika 4) površina za t ≤
0 je svega 0,0000034 što se može zanemariti.
Kad je t = m − 3,5σ = 0, tj. z = − 3,5 površina za t ≤ 0 je 0,00023 što je takođe malo, itd.
U praksi, otkazi u zoni tzv. negativnih vremena označavali bi otkaze koji su se desili pre nego što je sistem
pušten u korišćenje.
Tada se uzima da su ovakvi otkazi desili u vremenu t = 0, a njihovi uzroci su u greškama koje nije otkrila
kontrola kvaliteta.
Verovatnoća dešavanja ovakve vrste otkaza može se izračunati ako se zna koeficijent varijacije, tj. odnos
između standardne devijacije
σ
i srednje vrednosti
m.
Recipročna vrednost koeficijenta varijacije je
m / σ
, a vrednosti
t = 0
odgovara vrednost
z = − m / σ .
Prema tome, ostaje da se iz tablica pročita vrednost površine ispod normalne raspodele levo od
− m / σ
,
što će dati verovatno u dešavanja ovakve vrste otkaza.
Isto tako, u teoriji pouzdanosti vrednost za m uvek je pozitivna jer je to vremenska kategorija, dok u
ostalim primenama ova vrednost može biti od −∞ do ∞ .
O S O B I N E L A P L A S O V I H T R A N S F O R M A C I J A
Laplasova funkcija :
…………………………………….. (78)
Ima sledeće osobine:
1. P
= Φ(b) –Φ(a)
2. P
=
Φ(
) – Φ(
)=
= Φ(
) – Φ(-
=
= Φ(
) + 0,5 ……………………………………. (79)
5.2.2 LOG-NORMALNA RASPODELA
Ova raspodela proističe iz normalne raspodele .

52
R(t) = 1- Φ(z) = 1-
= 1-F(z) …………………………………………………… (85)
Funkcija intenziteta otkaza je onda:
λ(t) =
=
=
=
……………………………………. (86)
Ovo je dobra raspodela za proučavanje otkaza usled zamora materijala i habanja.
Slika 36
5.2.3 EKSPONENCIJALNA RASPODELA
53
Eksponencijalna raspodela je jedna od najjednostavnijih raspodela koje ćemo koristiti.
Funkcija gustine otkaza ima oblik:
............................................................................ (87)
Eksponencijalna raspodela je jednoparametarska raspodela, gde je parametar λ intenzitet otkaza.
F-ja gustine je monotono opadajuća funkcija, čija je vrednost u početnom trenutku f(0)=λ.
Slika 37 Funkcija gustine kod eksponencijalne raspodele
Na osnovu ranije poznatog izraza R(t) = 1- F(t) dobija se dalje:
.............................................................. (88)
Odnosno,

55
Slika 39 Izgled f-je intenziteta otkaza I pouzdanosti kod eksponencijalne raspodele
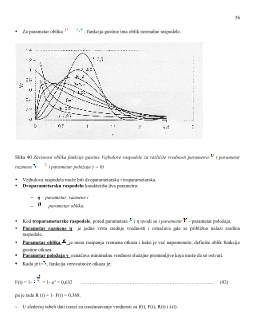
5.2.4 VEJBULOVA RASPODELA
Vejbulova raspodela je raspodela koja ima najveću primenu u praksi.
Razlog za ovo leži u činjenici da se svi modeli mogu aproksimirati ovom raspodelom.
Ovo najjasnije pokazuju razni oblici funkcije gustine.
U zavisnosti od parametara raspodele, parametra oblika menja se oblik funkcije gustine.
Za male vrednosti parametra oblika (
, opisuju se otkazi slično eksponencijalnoj tj. na na početku
je vrlo visoka učestanost, koja se kontinuirano smanjuje.
Za parametar oblika =1, dobija se eksponencijalna raspodela.
Kako raste, i veće je od 1, gustina u početnom trenutku ima vrednost f(t)=0, da bi zatim sa porastom
vremena dostigla maksimalnu vrednost, a nakon toga imala tendenciju pada.
Sa povećanjem vrednosti , maksimum funkcije gustine se pomera sve više u stranu.
56
Za parametar oblika
, funkcija gustine ima oblik normalne raspodele.
Slika 40
Zavisnost oblika funkcije gustine Vejbulove raspodele za različite vrednosti parametra ( parametar
razmene
i parametar položaja γ = 0)
Vejbulova raspodela može biti dvoparametarska i troparametarska.
Dvoparametarsku raspodelu
karakterišu dva parametra:
η
– parametar razmene i
parametar oblika.
Kod
troparametarske raspodele
, pored parametara i η uvodi se i
parametar
– parametar položaja.
Parametar razmene η
je jedna vrsta srednje vrednosti i označava gde se približno nalazi sredina
raspodele.
Parametar oblika
je mera rasipanja vremena otkaza i kako je već napomenuto, definiše oblik funkcije
gustine otkaza.
Parametar položaja γ
označava minimalnu vrednost slučajne promenljive koja može da se ostvari.
Kada je t= , funkcija verovatnoće otkaza je:
F(t) = 1-
= 1- e
-1
= 0,632 …………………………………………………………………….. (92)
pa je tada R (t) = 1- F(t) = 0,368.
U sledećoj tabeli dati izrazi za izračunavanje vrednosti za f(t), F(t), R(t) i λ(t).

58
Slika 43 Funkcije pouzdanosti Vejbulove raspodele za različite vrednosti parametara oblika ( parametar razmene
i
parametar položaja γ = 0)
Ukoliko se pažljivo pogledaju različiti oblici funkcije intenziteta otkaza, za različite vrednosti parametara oblika
, može se zaključiti da:
1 – pripada oblasti ranih otkaza,
= 1 – pripada oblasti slučajnih grešaka,
1 – pripada oblasti poznih otkaza.
59
Slika 44. Funkcija intenziteta otkaza Vejbulove raspodele za različite vrednosti parametra oblika (parametar razmene
i parametar položaja γ = 0)
Srednja vrednost Vejbulove raspodele se određuje pomoću gama funkcije.
m= η
(1+ ) ………………………………………………………………………… (93)
gde je:
(1+
) gama funkcija od 1+
Varijansa
Vejbulove raspodele se određuje prema izrazu:
=
…………………………………………………….
(94)

61
7. Kada intenzitet otkaza λ raste, a potom opada sa porastom vremena, treba proveriti
mogućnost aproksimacije logaritamsko-normalnim zakonom raspodele.
8. Ako intenzitet otkaza opada i ako je srednja vrednost manja od standardne devijacije ( m
), treba ispitati Vejbulov zakon raspodele sa parametrom oblika manjim od 1.
9. U slučaju da ni jedan od prethodnih uslova nije zadovoljen, a poznato je da polazni podaci
predstavljaju minimalne veličine, treba proveriti hipotezu o raspodeli minimalnih
( ekstremnih) vrednosti.
10. Kada je poznato da polazni podaci predstavljaju maksimalne ( ekstremne) slučajne veličine,
treba ispitati mogućnost aproksimacije raspodelom maksimalnih ( ekstremnih) vrednosti i/ili
gama raspodelom.
62
Slika 45 Algoritam za određivanje zakona raspodele

64
Numeričkim proračunom moguće je sračunati tačnu vrednost medijalnog ranga, prema izrazu:
0,5=
MR
k
( 1- MR)
n-k
………………………………………………… (96)
3. Uneti tačke [ti,F(t
i
)] u verovanosni papir pretpostavljene teorijske raspodele,
4. Povući aproksimativnu pravu liniju između ovako dobijenih tačaka.
Ukoliko se tačke nalaze na pravoj liniji, ili se gomilaju oko nje, odabrani model može biti korektan.
Sistemska odstupanja su upozorenje da model nije adekvatan.
Odluka o tome da tačke slede pravu liniju ima subjektivni karakter, i to je nedostatak metode
zasnovane na korišćenju verovatnosnog papira.
6.1.1. VEROVATNOSNI PAPIR NORMALNE RASPODELE
Sa verovatnosnog papira normalne raspodele, mogu se proceniti parametri normalne raspodele,
Apscisa verovatnosnog papira je linearna osa, a ordinata predstavlja funkciju verovatnoće otkaza
F(t),
Za procenu srednje vrednosti raspodele m treba povući liniju F(t)=50%, do preseka sa pravom
linijom, koja prolazi kroz ili između ucrtanih tačaka, a zatim vertikalno vući do apscise i očitati
vrednost srednje raspodele,
Standardna devijacija se dobija kao razlika vrednosti na apscisi koja odgovara tačkama:
F (t= m+ )= 84,13% i F (t)= 50%
……………………………………………. (97)
Na slici dole vidite verovatnosni papir normalne raspodele.
PRIMER 1:
65
Slika 46

67
Parametar na verovatnosnom papiru predstavlja odsečak od koordinatnog početka do preseka linije
sa apscisom, a srednja vrednost m se očitava za F(t) = 63,2%.
Parametar λ se određuje na osnovu izraza:
=
……………………………………………………………………….
(103)
Do gornjeg izraza se dolazi linearizacijom izraza:
1 - F(t) =
…………………………………………………………. (104)
Logaritmovanjem i sređivanjem se dobija :
ln (1- F(t)) = - λ·t + λ
· ……………………………………………………………. (105)
Kako je opšti oblik jednačine prave linije y=a·x+b, donosi se zaključak da je jednačina prave linije i
pri tome je:
x = t
a = -λ,
b =
y = ln [1-F(t)]
……………………………………………………. (106)
Pošto je F(t) = 63,2%, iz izraza F(t)= 1-
.
PRIMER
68
Slika 47

70
Nagib prave u verovatnosnom papiru definiše parametar oblika .
Parametar oblika može se očitati na desnoj ordinati, kada se Vejbulova parava paralelno prenese
kroz pol P.
Položaj pola P i podela linearne ordinate za parametar oblika , može se odrediti na osnovu
jednačina:
=
=
…………………………………………………….
(111)
Slika 48 Verovatnosni Vejbulov papir
Otkazi se prema, vremenu nastajanja, mogu podeliti na:
Rane,
Slučajne i
Pozne otkaze.
Funkcija intenziteta otkaza λ(t) ima oblik kade i mogu se sva tri područja preneti u Vejbulov
verovatnosni papir.
Sa verovatnosnog papira se za F(t)=63,2% koja je obeležena isprekidanim linijama, na apscisi očitava
parametar razmene η.
71
Slika 49 Kriva u obliku kade u Vejbulovom verovatnosnom papiru
Određivanje pola P
Za slučaj kada je = 1, dobija se:

73
Jedinična vrednost linearne ordinate odgovara verovatnoća pojave otkaza F(t) =0,2716% dvostruko
logaritmovane ordinate.
Troparametarska Vejbulova raspodela u Vejbulovom verovatnosnom papiru nije prava linija, već
konveksna kriva.
I ona može da se nacrta kao prava, kada se na apscisi nanese korigovano vreme ispravnog rada do
otkaza t- , gde je - parametar položaja ( bezotkazno vreme).
Na ovaj način se troparametarska raspodela pretvara u dvoparametarsku.
Parametar položaja može se odrediti iterativnim postupkom, prema
Dubey-u
.
Domen verovatnoće pojave otkaza treba podeliti na dva jednaka dela.
Tako se dobijaju 3 karakteristične vrednosti: t
1,
t
2
i t
3.
Znajući ove vrednosti,
parametar položaja može se odrediti izrazom
:
= t
2
-
……………………………………………………………. (117)
74
Slika 50 Troparametarska Vejbulova raspodela u Vejbulovom verovatnosnom papiru
PRIMER 3:

76
y = ln [-ln (1- F(t)] = ln ln
……………………………………………….. (119)
Primenom metode najmanjih kvadrata parametri a i b se izračunavaju prema sledećim izrazima:
a =
b=
, …………………………………………………………………... (120)
pri čemu je:
= a,
ln = -
=
…………………………………………………………………………………… (121)
6.3 INTERVAL POVERENJA
Ocene parametra , u vidu intervala, zovu se intervalne ocene.
Intervalna ocena zove se i interval poverenja.
Interval (
,
) je interval poverenja za parametar , sa nivoom poverenja P, ako sa unapred
zadatom verovatnoćom p možemo da tvrdimo da sadrži tačnu vrednosti parametra, ako važi:
P (
= P = 1- ……………………………………………………… (122)
Jasno je da je:
P (
= ………………………………………………………….. (123)
77
Verovatnoća
= 1-P,
se naziva i rizik, jer predstavlja verovatnoću da tačna vrednost parametra bude
izvan procenjenog intervala.
Granice intervala poverenja (
,
) se nazivaju granice poverenja, a širina intervala
predstavlja meru
preciznosti intervalne ocene parametra.
Što je širina intervala manja, to je preciznost intervalne ocene veća.
Interval poverenja nazivamo simetričnim, ako je
P (
) = P (
) =
……… (124)
6.3.1 OCENA SREDNJE VREDNOSTI NORMALNE RASPODELE SA POZNATOM
STANDARDNOM DEVIJACIJOM
Ako se pretpostavi da je iz skupa od 1000 elemenata ( osnovni skup), koji je raspoređen po zakonu
normalne raspodele
N ( m, )
, uzet uzorak obima n= 20 elemenata, onda srednja vrednost uzorka ,
odstupa od srednje vrednosti populacije m.
Ukoliko se uzorak proširi na 40 elemenata, dobiće se druga srednja vrednost uzorka, koja je bliža pravoj
srednjoj vrednosti, koja bi se dobila da se ispitivanje izvrši na celoj populaciji.
Normalna raspodela uzorka se može zapisati kao:
N(
,
=
, ………………………………………………………………. (125)
Ocena odstupanja izračunate srednje vrednosti od prave srednje vrednosti odgovarajuće raspodele, vrši
se na osnovu utvrđivanja granica, odnosno intervala poverenja.
F( z
α/2
)=1 – α/2

79
P ( ǀ
………………………………………………. (130)
Odnosno:
P ( - t·
m
+ t·
) = 1- …………………………………………… (131)
gde je – vrednost t raspodele za nivo rizika i za broj stepeni slobode f=n-1.
PRIMER:
6.4 PODRUČJE POVERENJA KOD VEJBULOVE RASPODELE
Svakom vremenu rada dodeljuje se jedinstvena verovatnoća otkaza u vidu srednje vrednosti- najčešće
medijalnog ranga, a onda se u Vejbulovom verovatnosnom papiru unose tačke [t
i
, F(t
i
)], između kojih se
povlači prava linija- Vejbulova prava.
Pošto se koristi medijalni rang, onda Vejbulova prava predstavlja pravu koja je najverovatnije u sredini,
jer se u 50% slučajeva stvarne prave nalaze ispod, a 50% iznad Vejbulove prave.
Na primer, 90% područje poverenja znači da se u 90 od 100 slučajeva posmatrana vrednost nalazi u
ovom području.
Ograničenjem područja poverenja dobijaju se granice poverenja.
Uobičajeno je da je područje poverenja simetrično oko medijane.
To onda znači da 90% područje poverenja poseduje 5% i 95% granicu poverenja za veličine ranga.
Vrednosti 5-% i 90-% ranga su date tabelarno.
Moguće vrednosti parametra razmene
η i
parametra oblika
β
mogu se približnim jednačinama
proračunati.
η
min =
η
5%
= η
MR
-
80
η
max =
η
95%
= η
MR
-
………………………………. (132)
7. STATISTIČKI TESTOVI
Ocena početne hipoteze o prihvatanju određenog zakona raspodele vrši se na verovatnosnom papiru
procenjivanjem da li sve unete tačke ( kumulativne učestanosti verovatnoće ili medijalnog ranga)
odgovaraju pravoj liniji.
Mogu se tolerisati izvesna odstupanja, bez obzira odakle potiču.
Da bi se u oceni ovih odstupanja dobila odgovarajuća sigurnost, uvode se statistički testovi.
Najpoznatiji testovi su: Kolmogorov-Smirnov ( d - test ) i Pirsonov χ
2
test.
7.1 KOLMOGOROV-SMIRNOV TEST
Test Kolmogorov- Smirnov se može koristiti za sve vrste kontinualnih raspodela, kao i za relativno mali
broj uzoraka.
Prilikom korišćenja ovog testa, treba poštovati sledeću proceduru:
1. Poređati podatke u rastućem nizu,
2. Utvrditi ukupan broj podataka,
3. Izračunati vrednosti empirijske funkcije pouzdanosti, odnosno verovatnoće otkaza,

82
n=∑ n
i=
n
1 +
n
2+ ----+
n
3 itd…
Ako se svaki od m podsklopova analizira posebno, kao da je u pitanju samostalni skup, onda je funkcija
pouzdanosti:
R
i
(t) =
=
=
+
+...+
.................................... (134)
7.4
PROGNOZIRANJE POUZDANOSTI
Za prognoziranje ponašanja konstrukcionih elemenata, sa gledišta pojave otkaza, neophodno je matematički
opisati zakone raspodele i gustine raspodele otkaza.
O pojavi otkaza kod nas postoji veoma malo sakupljenih i obrađenih informacija o pojavi otkaza mašinskih
elemenata.
Statistički parametri Vejbulove raspodele β, η i γ zavise od različitih slučajnih veličina:
(β, η i γ) = f ( oblik, materijal, obrada, opterećenje).
Ovo znači da za svaki slućaj korišćenja, konstrukcioni elementi imaju različite parametre Vejbulove
raspodele. Ispitivanja su pokazala da su parametri β i f
tβ
konstantni pri određenom opterećenju za pokazanu
vrstu oštećenja.
Parametri su povezani sa vrstom oštećenja, mehanizmom otkaza i delimično opterećenjem.
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































