studenti.rs home page

1

Seminarski rad iz predmeta Matematika 2

Tema : Izometrijske transformacije ravni

Profesor:                                 Student:

Banja Luka, decembar 2013.

2

Sadržaj:

Uvod............................................................................................................................................3

1. Osna simetrija..................................................................................................................3

2. Rotacija............................................................................................................................ 6

3. Centralna simetrija........................................................................................................... 9

4. Translacija......................................................................................................................10

background image

4

Def.2: Za dve figure Ŧ i Ŧ ' ravni α, kažemo da su simetrične u odnosu na pravu 

s

 te 

ravni(osno simetrične), ako svakoj tački M fugure Ŧ odgovara tačka M' figure Ŧ', 

tako da je J

s

(M)=M',i obrnuto, (sl.2).Pišemo J

s

 (Ŧ) = Ŧ '.

                              Sl.1.1                                                                Sl.1.2

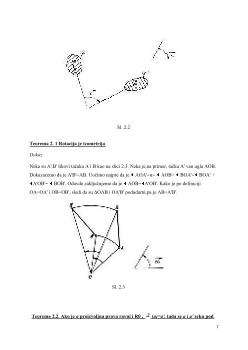
Teorema 1. Osna simetrija je izometrija ravni.

Dokaz

Neka je duž A'B' simetrična duži AB odnosu na pravu 

s. 

Treba dokazati da je AB=A'B'. Neka 

je S tačka prave

 s 

(sl.3) i neka

 

je O središte duži AA'. Touglovi AOS i A'OS su podudarni, pa 

je AS=A'S i   ASO =   A'SO. Slično se dokazuje da je BS=B'S i BSO1=  B'SO1

Iz ovoga zaključujemo da je   ASB =   A'SB',pa kako je AS = A'S i BS= B'S sledi da su 

trouglovi ABS i A'B'S podudarni(stav SUS).Stoga je AB=A'B'.

Sl. 1.3

Teorema 2. Osno simetrične prave su paralelne medju sobom(i paralelne osi) ili se seku 

Želiš da pročitaš svih 12 strana?

Prijavi se i preuzmi ceo dokument.

Prijavi se Napravi nalog

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.

Slični dokumenti