EVROPSKI UNIVERZITET BRČKO BiH
SEMINARSKI RAD
OSNOVI TELEKOMUNIKACIJE
Mentor : Student:
Prof.dr.Halid Žigić Asmir Zećić
Brčko,decembar,2014
Ugaona modulacija
2
Uvod…………………………………………………………………………………3
Spektar ugaono modulisanog signala……………………………………………......9
Frekvencijska modulacija i demodulacija…………………………………………..16
Frekvencijski demodulatori………………………………………………………....21
Simulacije u programskom paketu ORCAD……………………………………….29
Zaključak…………………………………………………………………………....38
Ugaona modulacija
4
Ako vršimo promjenu frekvencije nosećeg signala u ritmu informacionog(modulišućeg)
signala dobivamo frekvencijsku modulaciju (FM-Frequency Modulation).Ako pak
informacionim signalom utičemo na fazu nosećeg signala dobivamo faznu modulaciju (PM-
Phase Modulation).Jedna od osnovnih karakteristika ove modulacije je nelinearnost.Za razliku
od AM ugaona modulacija je slučaj gdje ne važi princip superpozicije te je riječ o nelinearnom
procesu zbog čega imamo i korišćenje termina eksponencijalna modulacija.Dakle u postupku
ugaone modulacije amplituda nosioca ostaje nepromjenjena a njegov ugao se modifikuje
modulišućim signalom i postaje karakterističan parameter u kojem je sadržana informacija.
Ako pođemo od izraza za sinusni nosilac:
u
0
(t)=
U
0
cos
(
ω
0
t
+
φ
(
t
)
)
Gdje faza direktno zavisi od modulišućeg signala:
φ
=
φ
(
t
)=
γ
(
u
m
(
t
)
)
Tada opšti izraz za ugaono modulisan signal iznosi:
u
(
t
)=
U
0
cos
ϕ
(
t
)=
U
0
cos
(
ω
0
t
+
φ
(
t
)
)
=
U
0
cos
(
ω
0
t
+
γ
[
u
m
(
t
)
]
)
Ugao
ϕ
(
t
)=
ω
0
t
+
φ
(
t
)=
ω
0
t
+
γ
[
u
m
(
t
)
]
=
ϕ
0
+
γ
[
u
m
(
t
)
]
=
ϕ
i
naziva se trenutna faza.
Veličina:
φ
(
t
)=
γ
[
u
m
(
t
)
]
=
δ ϕ
i
Koja predstavlja odstupanje trenutne faze
ϕ
i
od vrijednosti
ϕ
0
=
ω
0
t
naziva se trenutna devijacija
faze.
Izvod trenutne faze
ϕ
i
=
ϕ
(
t
)
po vremenu:
ω
i
=
d ϕ
i
dt
=
dϕ
(
t
)
dt
=
ω
0
+
dφ
(
t
)
dt
naziva se trenutna kružna učestanost ugaono modulisanog signala.
Odstupanje trenutne kružne učestanosti
ω
i
od kružne učestanosti nosioca
ω
0
Ugaona modulacija
5
dφ
(
t
)
dt
=
ω
i
−
ω
0
=
δ ω
i
predstavlja trenutnu devijaciju kružne učestanosti ugaono modulisanog signala.
Trenutna frekvencija ugaono modulisanog signala je:
f
i
=
ω
i
2
π
=
1
2
π
dϕ
(
t
)
dt
=
f
0
+
1
2
π
dφ
(
t
)
dt
Odstupanje trenutne frekvencijei
f
i
od frekvencije nosioca
f
0
:
1
2
π
dϕ
(
t
)
dt
=
f
i
−
f
0
=
δ f
i
nazivamo trenutnom devijacijom frekvencije.
Dakle kod fazne modulacije trenutna devijacija faze je direktno proporcionalna modulišućem
signalu dok je kod frekvencijske modulacije trenutna devijacija frekvencije proporcionalna
modulišućem signalu.
Neka je dat izraz za sinusni nosilac u obliku:
s
(
t
)=
A
0
cos
[
θ
(
t
)
]
=
¿
A
0
cos
(
ω
0
t
+
φ
(
t
)
)
¿
Pretpostavimo da se njegov trenutni fazni ugao linearno mijenja u zavisnosti od modulišućeg
signala s
m
(t):
θ
PM
(
t
)=
ω
0
t
+
K
φ
s
m
(
t
)=
θ
0
+
δθ
(
t
)
Trenutna ucestanost fazno modulisanog signala je:
ω
PM
(
t
)=
d θ
PM
(
t
)
dt
=
ω
0
+
K
φ
d s
m
(
t
)
dt
gdje je
K
φ
konstanta proporcionalnosti.
Ako modulišući signal predstavimo kao:
s
m
(
t
)=
A
m
m
(
t
)
A
m
=
|
s
m
(
t
)
|
max
Ugaona modulacija
7
φ
(
t
)=
K
φ
s
m
(
t
)
fazna modulacija
φ
(
t
)=
K
f
∫
s
m
(
t
)
dt frekvencijska modulacija
Tip modulacije
Modulišući signal
Ugaono modulisani signal
PM
V(t)
V
0
cos[ω
0
t+KV(t)]
FM
V(t)
V
0
cos[ω
0
t+2πK
1
ʃ V(t)dt]
PM
V
a
cosω
a
t
V
0
cos[ω
0
t+KV
a
cosω
a
t]
FM
- V
a
cosω
a
t
V
0
cos(ω
0
t+(2πK
1
V
a
)/ω
a
cos ω
a
t)
FM
V
a
cosω
a
t
V
0
cos(ω
0
t+(2πK
1
V
a
)/ω
a
sin ω
a
t)
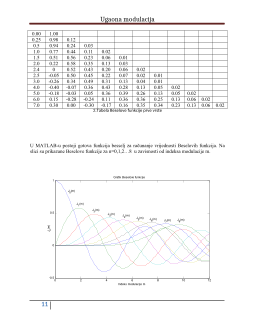
1.Tabela Jednačine za fazno i frekvencijski modulisane signale
Primjer frekvencijske modulacije u MATLAB-u
Za generisanje FM signala koristili smo slijedeći izraz:
s
(
t
)=
A
c
cos
[
2
π f
c
t
+
2
π K
f
∫
0
t
m
(
t
)
dt
]
Signal poruke ima vrijednost amplitude 1 dok je vrijednost kružne učestanosti podešena na
1rad/s. Za noseći talas imamo parametere ω
c
=10 rad/s dok je vrijednost amplitude podešena na
1.Faktor modulacije iznosi 1.
>> wm=1;
>> wc=10;
>> Fm=wm/(2*pi);
>> dt=1e-3;
