
Motori naizmenicne struje
1
ASINHRONI MOTORI
Od Teslinog pronalaska pre više od 120 godina, pa sve do danas asinhroni motor je najvažniji
pogonski motor u industriji i drugim primenama u pogonima konstantne brzine. Osnovni uzroci tome su
njihova sigurnost u pogonu, jednostavnost konstrukcije kao i pristupa
č
na cena. Me
đ
utim, sa razvojem
energetske elektronike poslednjih decenija, pre svega invertora sa poluprovodni
č
kim prekida
č
ima,
tiristorima i snažnim tranzistorima, ovaj motor jednostavne konstrukcije po
č
inje da osvaja i polja gde su
suvereno dominirali motori za jednosmernu struju – pogone sa promenljivom brzinom. Šta više,
uvo
đ
enjem mikrokompjutera poslednjih godina u regulacioni deo pogona, kojim se omogu
ć
ava da se uz
nevelike dodatne troškove postigne izvo
đ
enje i veoma složenih algoritama upravljanja, pogoni sa
asinhronim motorima, kao uostalom i sinhronim motorima raznih vrsta, postaju konkurentni pogonima za
jednosmernu struju
č
ak i u pogledu dinami
č
kog odziva.
PRINCIP RADA ASINHRONOG MOTORA
Pre nego što objasnimo princip rada asinhronog motora razmotrimo proces dobijanja obrtnog magnetnog
polja u asinhronim motorima sa trofaznim namotom statora spojednim u zvezdu (
Sl. 4.1.1
). Sa slike
vidimo da je svaki namot predstavljen u obliku jednog provodnika a jedan u odnosu na drugi su prostorno
pomereni za 2
π
/3. Iz izvora napajanja namotima statora se dovodi trofazni sistem napona pod
č
ijim
dejstvom kroz nammote proti
č
e trofazni sistem struja koje su me
đ
usobno vremenski pomerene za T/3,
odnosno:
⎟
⎠
⎞
⎜
⎝
⎛
−
=
⎟
⎠
⎞
⎜
⎝
⎛
−
=
=
3
4
sin
3
2
sin
sin
π
ω
ω
π
ω
ω
ω
t
t
I
I
t
t
I
I
t
I
I
m
C
m
B
m
A
(4,1,1)
Svaka od ovih struja
ć
e stvarati svoje magnetno polje odnosno magnetni fluks koji se naziva pulziraju
ć
im.
Na
Sl.4.1.1
je prikazan pozitivan smer struja u linijskim provodnicima i namotima statora kao i smer
faznih magnetnih flukseva saglasno pozitivnom smeru faznih
struja. Fazni magnetni fluks je uvek usmeren po osnim
linijama statora bez obzira da li je pozitivan ili negativan i
uvek prati promenu struje usled koje nastaje. Pri
sinusoidalnoj promeni fazne struje u namotima, magnetni
fluks faze se tako
đ
e menja po sinusnom zakonu u vremenu.
Ako pretpostavimo da struje
i
A
,
i
B
i
i
C
imaju isti fazni stav,
odnosno da su u svakom trenutku vremena jednake po
vrednosti i smeru, to
ć
e i magnetni fluksevi uslovljeni tim
strujama tako
đ
e u svakom trenutku vremena biti jednaki po
vrednosti a po smeru pomereni za ugao od 120º.Ukupan fluks
u takvom magnetnom kolu je jedan nuli. Kako u praksi kroz
namote proti
č
e trofazni sistem struja (
Sl.4.1.2
) o
č
igledno je
A
I
I
I
3
0
0
−
=
=
Sl. 4.1.1. Šema magnetnog kola
asinhronog motora: 1-rotor; 2-stator
2
da ukupni magnetni fluks nije jednak nuli. Za odre
đ
ivanje vrednosti ukupnog magnetnog fluksa
neophodno je raspolagati vremenskim zavisnostima promene faznih struja (
Sl.4.1.2
) odnosno faznih
flukseva. Vidi se da u trenutku
t
0
= 0 struje
i
A0
,
i
B0
i
i
C0
i imaju slede
ć
e vrednosti
0
0
=
A
i
(4.1.2)
m
B
I
i
2
3
0
−
=
(4.1.3)
m
C
I
i
2
3
0
=
(4.1.4)
Saglasno sa ovim magnetni fluks faze A je nula a magnetni fluksevi faza B i C su jednaki po amplitudi i
iznose:
(4.1.5)
Gde je maksimalna vrednost fluksa po fazi. Kako
je struja
i
B0
negativna to je i magnetni fluks
Φ
B
suprotan uslovno pozitivnom smeru prikazanom
na
Sl.4.1.1
. Struja
i
C0
je pozitivna pa se i fluks
Φ
C
poklapa sa uslovno pozitivnim smerom prikazanim
na istoj slici. Novonastalo stanje sa ozna
č
enim
smerovima struja i flukseva je prikazano na
Sl.4.1.3a
, a vrednost i smer rezultatnog magnetnog
fluksa koji je nastao sabiranjem pulziraju
ć
ih
flukseva pojedinih faza je prikazan na
Sl. 4.1.3b.
Smer struje u provodnicima B i Z je isti i oni
u
č
estvuju u stvaranju jednog fluksa
č
iji je smer
odre
đ
en pravilom desnog zavrtnja. Ovaj fluks se
zatvara kroz stator i rotor obuhvataju
ć
i provodnike B i Z (
Sl.4.1.3a
). To se odnosi i na struje koje proti
č
u
provodnicima C iY. Sa
Sl. 4.1.3b
se vidi da je u trenutku
t
0
= 0 ukupni magnetni fluks F 1,5 puta ve
ć
i od
maksimalne vrednosti faznog fluksa i usmeren je vertikalno naviše
(4.1.6.)
U trenutku
t
1
= T/12 vrednost struja
i
A1
,
i
B1
i
i
C1
u namotajima je:
(4.1.7.)
(4.1.8.)
Ovim vrednostima struja odgovaraju vrednosti magnetnih flukseva faza:
(4.1.9.)
Sl. 4.1.2 Vremenska promena struje u faznim
namotajima
m
m
C
B
Φ
=
Φ
−
=
Φ
=
Φ
867
.
0
2
3
B
B
Φ
=
Φ
=
Φ
5
.
1
30
cos
2
o
m
B
m
C
A
I
i
I
i
i
−
=
=
=
1
1
1
5
.
0
m
B
m
C
A
Φ
=
Φ
Φ
=
Φ
=
Φ
5
.
0
4
sekundi ima
f
perioda, to
ć
e obrtno magnetno polje u toku jedne sekunde napraviti
f/p
obrtaja. Kako se
brzina obrtanja obi
č
no izražava u minuti, to
ć
e brzina obrtnog magnetnog polja u minuti iznositi:
(4.1.12.)
Obzirom da je obrtno magnetno polje promenljivo u prostoru i vremenu to
ć
e isto biti pra
ć
eno
indukovanim elektri
č
nim poljem koje
ć
e usled pojave elektromagnetne indukcije dovesti do indukovanja
elektromotorne sile kako u namotu statora (
E
1
- elektromotorna sila samoindukcije), tako i u namotu
rotora (
E
2
- elektromotorna sila me
đ
uindukcije). Smer elektromotorne sile E koja se indukuje u namotu
rotora objasni
ć
emo primenom dinami
č
ke indukcije (i ako se u datom slu
č
aju radi o stati
č
koj indukciji).
Naime ako provodnik stoji a magnetno polje se kre
ć
e ugaonom brzinom
Ω
1
(
Sl.4.1.4b
) to možemo
posmatrati kao relativno kretanje, a to zna
č
i da je magnetno polje nepokretno a da se provodnik kre
ć
e u
suprotnom smeru od smera obrtnog magnetnog polja brzinom
v
, kao na
Sl.4.1.4b
.
Sl. 4.1.4 Principijelna šema rada asinhronog motora
Ako se provodnik kre
ć
e brzinom
v
u stalnom magnetnom polju
B
, to
ć
emo smer indukovane
elektromotorne sile koja
ć
e se po zakonu dinami
č
ke elektromagnetne indukcije indukovati u datom
provodniku odrediti uz pomo
ć
izraza
( )
l
d
B
v
l
d
E
E
ind
r
r
r
r
r
⋅
×
=
⋅
=
∫
∫
2
(4.1.13.)
Imaju
ć
i u vidu pravila vektorskog proizvoda vektora
v
i
B
to
ć
e pravac indukovane elektromotorne sile
biti u pravcu ravni koja je normalna na ravan vektora
v
i
B
a smer odre
đ
ujemo primenom pravila desne
zavojnice i to tako da se vektor
v
najkra
ć
im putem poklopi sa vektorom
B
. Smer kretanja desne zavojnice
predstavlja i smer indukovane elektromotorne sile
E
2
u namotu rotora. Imaju
ć
i u vidu da su namoti rotora
zatvoreni to
ć
e elektromotorna sila
E
2
kroz date namote u istom smeru proterati struju
I
2
,
č
ija je aktivna
komponenta istog smera kao i
E
2
. Kako kroz provodnike rotora proti
č
e struja
I
2
to
ć
e na iste magnetno
polje statora delovati elektromagnetnom silom.
B
l
d
I
F
r
r
r
×
=
∫
2
(4.1.14.)
p
f
n
60
1
=
5
Iz izraza za elektromagnetnu silu vidimo da je pravac sile normalan na ravan u kojoj se nalaze vektori
dl
i
B
a smer sile odre
đ
ujemo pravilom desne zavojnice, okre
ć
u
ć
i zavojnicu u smeru koji se najkra
ć
im putem
vektor
dl
poklopi sa vektorom
B
. Smer napredovanja desne zavojnice odre
đ
uje smer sile
F
(Sl.4.1.4c
).
Na
osnovu smera elektromagnetne sile F vidimo da ona pokre
ć
e rotor u smeru obrtanja obrtnog
magnetnog polja
. Ovo se dešava sa svim provodnicima po obimu rotora, a zbir svih proizvoda sile i
polupre
č
nika rotora daje obrtni elektromagnetni moment motora
M
m
.
Na osnovu gore izloženog zaklju
č
ujemo, da kad asinhroni motor priklju
č
imo na trofaznu mrežu, rotor
datog motora se obr
ć
e u smeru obrtnog magnetnog polja. Pri tome se rotor motora obr
ć
e brzinom manjom
od sinhrone brzine obrtnog magnetnog polja, što je i razumljivo jer kada bi se i rotor obrtao sinhronom
brzinom ne bi bilo relativnog kretanja izme
đ
u rotora i obrtnog magnetnog polja odnosno vektor brzine bio
bi jednak nuli te na osnovu izraza (4.1.13.) zaklju
č
ujemo da bi indukovana elektri
č
na sila
E
2
tako
đ
e bila
jednaka nuli, a time ne bi bilo ni struje u namotima rotora. Kao posledica toga ne bi postojao ni obrtni
elektromagnetni moment motora. Usled toga rotor bi po
č
eo zaostajati, odnosno obrtati se nižom brzinom
što bi dovelo do pojave relativnog kretanja rotora u odnosu na obrtno magnetno polje
č
ime bi ponovo bili
stvoreni uslovi za indukovanje elektromotorne sile
E
2
a time i proticanja struje
I
2
kroz namote rotora te
kona
č
no i pojave obrtnog momenta motora. Time dolazimo do drugog bitnog zaklju
č
ka a to je da
rotor
motora nikada ne može dosti
ć
i brzinu obrtnog magnetnog polja statora
.
Kada motor radi neoptere
ć
en odnosno u praznom hodu, obrtni moment motora savladava samo moment
usled trenja i ventilacije, koji je relativno mali te se rotor motora vrti brzinom bliskoj sinhronoj brzini
obrtnog magnetnog polja. Ako sa n ozna
č
imo brzinu obrtanja rotora, tada odnos razlike brzina obrtnog
magnetnog polja i brzine rotora prema sinhronoj brzini nazivamo
relativno klizanje
:
1
1
n
n
n
s
−
=
(4.1.15.)
Vrednost klizanja ve
ć
ih motora kre
ć
e se u granicama od 0,01 do 0,03 a kod manjih motora od 0,03 do
0,08. Dati motori su dobili naziv asinhroni upravo zbog toga što mu se rotor ne obr
ć
e istom brzinom kao i
obrtno magnetno polje.
Ako sa
f
1
ozna
č
imo u
č
estanost elektri
č
nih veli
č
ina statora, postavlja se pitanje kolika je u
č
estanost
f
2
indukovane elektromotorne sile
E
2
. Da bi smo je odredili neophodno je najpre odrediti relativnu brzinu
obrtnog polja statora u odnosu na rotor, a ona iznosi:
n
n
n
−
=
1
2
(4.1.16.)
Brzina
n
2
fizi
č
ki predstavlja brzinu presecanja provodnika rotora od strane obrtnog magnetnog polja
statora. Time
ć
e u
č
estanost
f
2
indukovane elektromotorne sile
E
2
iznositi:
(
)
1
1
1
1
1
1
1
2
2
60
60
60
f
s
n
n
n
pn
n
n
n
n
p
pn
f
⋅
=
−
⋅
=
⋅
−
=
=
(4.1.17.)
Vidimo da u
č
estanost
f
2
elektri
č
nih i magnetnih veli
č
ina koje se javljaju na rotoru, dobijemo kad
u
č
estanost statora
f
1
pomnožimo sa klizanjem
s
. Imaju
ć
i u vidu vrednosti klizanja
s
, jasno je da je red
veli
č
ine u
č
estanosti rotora
f
2
vrlo mali i iznosi svega nekoliko herca u normalnom režimu rada motora.
Obzirom da gubici snage u gvož
đ
u rotora zavise od kvadrata u
č
estanosti
f
2
o
č
igledno je da
ć
e oni biti vrlo

7
‐
Da je ustaljeno stanje,
‐
Napon i u
č
estanost napajanja konstantni,
‐
Statorska otpornost se može zanemariti,
‐
Struja magne
ć
enja se može zanemariti
‐
Parametri mašine (
R
r
,
L
s
i
L
r
) ne zavise od brzine.
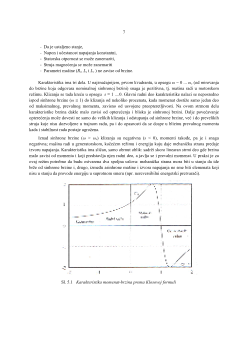
Karakteristika ima tri dela. U najzna
č
ajnijem, prvom kvadrantu, u opsegu
ω
= 0 ...
ω
s
(od mirovanja
do brzine koja odgovara nominalnoj sinhronoj brzini) snaga je pozitivna, tj. mašina radi u motorskom
režimu. Klizanja se tada kre
ć
u u opsegu
s
= 1 ....0. Glavni radni deo karakteristike nalazi se neposredno
ispod sinhrone brzine (
ω
≤
1) do klizanja od nekoliko procenata, kada momenat dostiže samo jedan deo
od maksimalnog, prevalnog momenta, zavisno od usvojene preopteretljivosti. Na ovom strmom delu
karakteristike brzina dakle malo zavisi od optere
ć
enja i bliska je sinhronoj brzini. Dalje pove
ć
avanje
optere
ć
enja može dovesti ne samo do velikih klizanja i odstupanja od sinhrone brzine, ve
ć
i do prevelikih
struja koje nisu dozvoljene u trajnom radu, pa i do opasnosti da se dospe u blizinu prevalnog momenta
kada i stabilnost rada postaje ugrožena.
Iznad sinhrone brzine (
ω
>
ω
s
) klizanja su negativna (
s
< 0), momenti tako
đ
e, pa je i snaga
negativna; mašina radi u generatorskom, ko
č
e
ć
em režimu i energiju koju daje mehani
č
ka strana predaje
izvoru napajanja. Karakteristika ima sli
č
an, samo obrnut oblik: sadrži skoro linearan strmi deo gde brzina
malo zavisi od momenta i koji predstavlja njen radni deo, a javlja se i prevalni momenat. U praksi je za
ovaj režim potrebno da budu ostvarena dva spoljna uslova: mehani
č
ka strana mora biti u stanju da ide
brže od sinhrone brzine i, drugo, izme
đ
u asinhrone mašine i izvora napajanja ne sme biti elemenata koji
nisu u stanju da provode energiju u suprotnom smeru (npr. nereversibilni energetski pretvara
č
i).
Sl. 5.1
Karakteristika momenat-brzina prema Klosovoj formuli
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































