Fizičko tehnička merenja
– Laboratorijski vežba – Sistemi I i II reda
strana 1 od 6
IV VEŽBA
4.
SNIMANJE KARAKTERIST
IKA DINAMIČKIH SISTE
MA PRVOG I DRUGOG
REDA
Dinamičke karakteristike većine senzora se mogu opisati diferencijalnim jednačinama prvog ili drugog
reda. Sisteme prvog reda karakteriše vremenska konstana
koja predstavlja vreme potrebno da izlaz
pretvača dostigne 63.2 % vrednosti koje odgovara ustaljenom stanju, u odnosu na početak odskočne
pobude kojoj je podvrgnut posmatrani pretvarač. Dinamičko ponašanje sistema drugog reda opisuje
koeficijent prigušenja ko
ji zavisi od sredine u kojoj se pretvarač nalazi i sopstvene učestanosti koja zavisi
od konstrukcije pretvarača. Za prigušenja manja od 1, pri impulsnoj pobudi, odziv pretvarača su
kvaziperiodične oscilacije, kod kojih amplituda oscilacija ekspo
nencijalno opada sa vremenom, a što je
prigušenje veće to i oscilacije brže isčezavaju.
4.1.
ZADATAK VEŽBE
a)
Sistem I
reda. Izvršiti odskočnu pobudu silicijumskog temperaturskog senzora i na bazi odziva
snimljenog računarom odrediti vremensku konstantu
senzora
s]
[
, bez i sa zaštitnog sloja.
b)
Sistem II reda. Ostvariti impulsnu pobudu pretvara
č
a sile (konzole sa dve zalepljene merne trake) i
odrediti sopstvenu u
č
estanost
s
i koeficijent prigušenja
ξ
, pretvara
č
a. Eksperiment izvesti za dve
vrednosti prigušenja amortizera.
4.2.
TEORIJSKI OSNOVI
4.2.1.
SISTEMI PRVOG REDA
Tipični predstavnici dinamičkih sistema prvog reda su termometri i srodni tipovi senzora čiji se rad zasniva
na razmeni toplote sa okolinom. Posmatra se temperaturski senzor mase
m ,
specifične toplote
c
i
spoljašnje površine
S
. Ako se senzor nalazi u fluidu čija temperatura iznosi
a
T
u intervalu
dt
senzor
prima od fluida količinu toplote
dt
T
T
hS
dQ
a
, gde je
T
temperatura senzora, a
h
koeficijent
prenosa toplote na površini fluid-senzor. Ista koli
č
ina toplote se akumulira u senzoru
mcdT
dt
T
T
hS
dQ
a
(4.1)
gde je
dT
elementaran porast temperature senzora u intervalu
dt
. Iz (4.1) dolazi se do poznate
diferencijalne jednafine prvog reda
a
T
T
dt
dT
(4.2)
gde je
hS
mc
/
vremenska konstanta.
Posmatra se termometar sa linearnom statičkom karakteristikom, čiji je izlazni napon
KT
U
i
(4.3)
Konstanta
C]
/
V
[
K
naziva se statička osetljivost. Ako se termometar
nalazi u ustaljenom stanju na
temperaturi tačke leda
C
0
1
T
i izloži skokovitoj promeni spuštanjem u kupatilo na temperaturi
2
T
iz
(4.2) i (4.3) dobija se izlazni napon
Fizičko tehnička merenja
– Laboratorijski vežba – Sistemi I i II reda
strana 2 od 6
/
2
1
t
i
i
e
U
t
KT
t
U
(4.4)
gde je
2
2
KT
Ui
maksimalni izlazni napon koji se dobija nakon dužeg boravka senzora na temperaturi
2
T
.
Dijagram izlaznog napona (4.4) prikazanje na sl.4.1 a. Ako je
t
iz (4.4) sledi
1
2
2
( )
(1
)
0.632
i
i
i
u
U
e
U
. Polazeći od snimljenog odziva na odskočnu pobudu, sl.
4.1 a, vremenska
konstanta se može najlakše proceniti kao apscisa pri kojoj promena napona iznosi 63.2 % od njegove
maksimalne vre
dnosti. Ovaj način određivanja
je veoma brz, ali ima i nedostataka. Naime, koristi se
samo jedna tačka dijagrama, pri čemu
nema provere da li snimljeni odziv odgovara izrazu (4.4), tj. da li je u
pitanju zaista sistem I
reda. Bolji metod za izračunavanje vremenske konstante je da se rezultati merenja
predstave u linearizovanoj formi, tj. u polulogaritamskoj razmeri.
t
U
t
u
i
i
2
1
ln
(4.5)
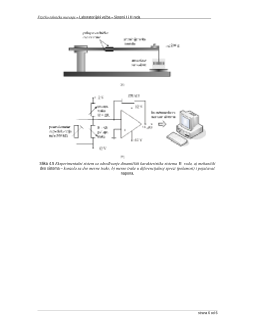
Slika 4.1 a) Odziv sistema prvog reda na odsko
č
nu pobudu, b) linearizovani dijagram
iz koga se pomoću
svih snimljenih tačaka izračunava vremenska konstanta
.
Koriste
ć
i izraz (4.5) eksponencijalni dijagram sa sl.4.1 a pretvara se u linearan sl.4.1 b. Pri crtanju
polulogaritamskog dijagrama treba koristiti samo tačke sa strmog dela karakteristike
, jer pri
2
i
i
U
t
u
l
ogaritamski član teži beskonačnosti.
Linearni dijagram crta se kao optimalna prava, tj. primenom metode
najmanjih kvadrata odstupanja. Vremenska konstanta
predstavlja recipročnu vrednost nagiba optimalne
prave.
Ovaj metod dobijanja
je pogodan iz dva razloga, a) vremenska konstanta se dobija na osnovu svih
snimljenih tačaka, čime se postiže efekat usrednjavanja. b) Ako dijagram u polulogaritamskoj razmeri ima
približno linearni oblik, onda se zaista radi o sistemu prvog reda. Ako dijagram znatnije odstupa od prave,
to ukazuje da nije u pitanju sistem I reda.
4.2.2.
SISTEMI DRUGOG REDA
U sisteme drugog reda spada
već
i
na senzora sile, pritiska, ubrzanja i drugih srodnih veličina. Pored
elastičnih i viskoznih sila, kod ovih senzora dolazi do izražaja inercijalna sila usled ubrzanog kretanja
pokretnih delova. Linearni sistem za merenje sile
modelira se pomoću opruge koeficijenta krutosti
[N/m]
k
, viskoznog elementa-
prigušivača,
sa koeficijentom viskoznog trenja
[Ns/m]
c
i inercijalnog
elementa mase
m
. Izlazni napon
i
U
senzora sile
)
(
t
F
dat je diferencijalnom jednačinom drugog reda
)
(
2
2
2
2
2
t
KF
u
dt
du
dt
u
d
s
i
s
i
s
i
(4.6)
gde je
m
k
s
(4.7)
sopstvena kružna frekvencija, a
