
Test funkcije
Uvod
Test-funkcija
je poznata ulazna veličina (funkcija) koja služi za ispitivanje ponašanja elemenata,
odnosno sistema upravljanja.
Upravljanje
je skup upravljačkih procesa kojima se realizuje funkcija cilja sistema.
Najčešće korišćene test-funkcije su:
odskočna,
impulsna,
nagibna i
harmonijska funkcija.
U ovom radu opisaćemo svaku od navedenih test-funkcija kao i odziv sistema na test
funkcije.Najčešće primenjivana test funkcija je odskočna funkcija. U radu smo je opširnije predstavili
kao i ostale navedene funkcije.
1. Test funkcije
Za ispitivanje ponašanja elemenata sistema upravljanja, na ulaz sistema se dovodi poznata ulazna
veličina, test-funkcija, pa se o ponašanju sistema zaključuje na osnovu izlazne veličine, odnosno odziva
na test- funkciju. Najčešće korišćene test-funkcije su: odskočna, impulsna, nagibna i harmonijska
funkcija.
1.1. Odskočna funkcija
Odskočna funkcija se definiše relacijom
(Savić, Stanković, 2012)
:
(1.1)
gde je:
- konstantna amplituda;
- jedinična odskočna funkcija definisana na sledeći način:
(1.2)
Kada je
relacija (3.1) postaje:
(1.3)
i definiše jediničnu odskočnu funkciju.
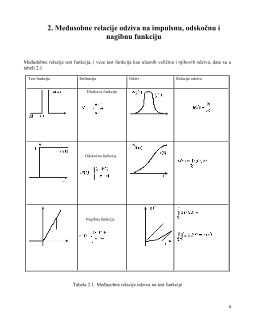
Na slici 1.1. prikazani su odgovarajući grafici odskočne funkcije:
Slika 1.1. Odskočna funkcija
Odskočna funkcija je najčešće korišćena test-funkcija. Pri tome, poseban značaj ima odskočni odziv
na jediničnu odskočnu funkciju, kojim se definiše
prelazna karakteristika
ili
vremenska
karakteristika
ispitivanog sistema.
Odskočni odziv
je rešenje linearne diferencijalne jednačine:
(1.4.)
za
i početne uslove:
Prelazna karakteristika
h(t)
dobija se kada se odskočni odziv
podeli amplitudom odskočne
funkcije:
(1.5.)
Prema tome, prelazna karakteristika predstavlja odziv sistema na jediničnu odskočnu funkciju.
1
Za slučaj kada je:
(1.9)
na osnovu jednačina (1.7) i (1.9), u graničnom slučaju kada
, dobija se:
(1.10)
gde je:
(1.11.)
Funkcija
(t
)
naziva se jedinična impulsna ili Dirakova
-funkcija.
Relacija (1.10) može da se napiše u obliku:
(1.12)
Odziv na jediničnu impulsnu funkciju, prema relaciji (1.8), je:
(1.13)
U graničnom slučaju kada
, odziv (1.13) dobija oblik:
(1.14)
Ukoliko je funkcija
h(t)
diferencijabilna, biće:
(1.15)
Impulsni odziv jednak je izvodu odziva na jediničnu odskočnu funkciju.
3
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































