
Fizikalne veličine
PREDAVANJA – FIZIKA I, Doc.Dr.Sc. Suada BIKI
Ć
1.
Fizikalne veli
č
ine
1.1
Skalarne i vektorske veli
č
ine
Skalarne veli
č
ine su potpuno odre
đ
ene svojom broj
č
anom vrijednoš
ć
u i odgovaraju
ć
om jedinico ( dužina,
zapremina, specifi
č
na gusto
ć
a, temperatura, masa, frekvencija, rad, snaga, vrijeme itd. ).
Za potpuno odre
đ
ivanje vektorskih veli
č
ina moramo poznavati pravac, smjer i intenzitet. Broj
č
ana
vrijednost fizikalne veli
č
ine izražena je u odre
đ
enim jedinicama i zove se iznos, modul, intenzitet ili
apsolutna vrijednost.
Mnoge su fizikalne veli
č
ine vektori kao što su: brzina, ubrzanje, koli
č
ina kretanja (impuls), moment
koli
č
ine kretanja ( moment impulsa), sila, ugaona brzina itd.
Vektor predstavljamo usmjerenom dužinom, u odgovaraju
ć
em mjerilu, koja daje iznos vektora, dok smjer
strelice predstavlja smjer vektora ( Slika 1.1 )
Oznaka vektorske veli
č
ine ili
v
.
v
→
Oznaka modula
v
ili
.
v
→
A B AB
Slika 1.1 Grafi
č
ko predstavljanje vektora i na
č
in pisanja
Definicija kolinearnosti: Vektori su kolinearni ako su im pravci paralelni pri
č
emu mogu imati isti smjer
ili suprotan smjer. Kolinearne vektore istog smjera i intenziteta smatramo jednakim. Takve vektore
možemo pomjerati po pravcu i paralelno translatirati te im se tada ne mijenja ni pravac ni smjer.
-
Sabiranje vektora:
a b
c
→ →
→
+ =
.
Grafi
č
ki vektore sabiremo tako da po
č
etak drugog vektora paralelnom translacijom dovedemo na kraj
prvog vektora: rezultuju
ć
i vektor ide od po
č
etka prvog vektora do kraja drugog vektora
( Slika 1.2 )
d
→
a b
c
→ →
→
+ =
b
→
R
a b c d
→
→ → → →
= + + +
c
→
b
→
a
→
a
→
a b c
+ ≠
R a b c d
≠ + + +
Slika 1.2 Grafi
č
ko sabiranje vektora
Modul rezultuju
ć
eg vektora jednaka je zbiru modula pojedinih vektora koji se sabiraju samo u slu
č
aju
kada su oni kolinearni i istog smjera.
Drugi na
č
in sabiranja vektora je metod paralelograma prikazan na Slici 1.3.
b
→
ϕ
ϑ
c
→
c
a b
→
→ →
= +
a
→
Slika 1.3 Metod paralelograma
1
NE RE
CENZIRANA S
K
RIPTA!
PREDAVANJA – FIZIKA I, Doc.Dr.Sc. Suada BIKI
Ć
- Oduzimanje vektora se svodi na sabiranje vektora što je predstavljeno na Slici 1.4.
b
→
a b
→ →
−
b
→
a b
→ →
−
a
→
a
→
a
b
→
→
+ −
(
)
−
→
b
Slika 1.4 Oduzimanje vektora
-
Množenje vektora skalarom: Vektor množi se pozitivnim skalarom
a
→
α
tako da mu se intenzitet
pomnoži sa tim skalarom, a smjer i pravac rezultuju
ć
eg vektora ostaje isti kao i u vektora . Pri
množenju sa negativnim skalarom (
a
→
α
<
0
) smjer vektora
α
a
→
je suprotan smjeru vektora , a pravac
ostaje nepromjenjen.
a
→
-
Množenje vektora vektorom može kao rezultat dati skalar pa se to množenje vektora definira kao
skalarni proizvod dva vektora koji je dat relacijom
.
c
a b
ab
a b
= ⋅ =
∠
→ →
→ →
cos(
, )
-
Množenje vektora vektorom kao rezultat daje vektor ( Slika 1.5). Taj proizvod se definira kao
vektorski proizvod dva vektora.
c
→
c
a b
→
→ →
= ×
, vektor je normalan
c
→
na ravan u kojoj leže vektori i .
a
→
b
→
b
→
c ab
a b
=
∠
→ →
sin(
, )
a
→
Slika 1.5 Vektorski proizvod dva vektora
Sa Slike 1.3 vidi se da je
c
a b
→
→ →
= +
.
Sada se ova relacija kvadrira pa se dobija
c c
a a b b
a b
c
a
b
ab
c
a
b
ab
→ →
→ → → →
→ →
⋅ = ⋅ + ⋅ +
⋅ ⇒
=
+
+
⇒
=
+
+
2
2
2
2
2
2
2
2
cos
cos .
ϕ
ϕ
Dalje se može ra
č
unati
c a
b
c
a
ac
b
c
a
b
ac
→ →
→
− =
+
−
=
⇒
⇒
=
+
−
2
2
2
2
2
2
2
2
cos
cos
.
ϑ
ϑ
1.2
Komponente vektora. Koordinatni sistem
2
NE RE
CENZIRANA S
K
RIPTA!
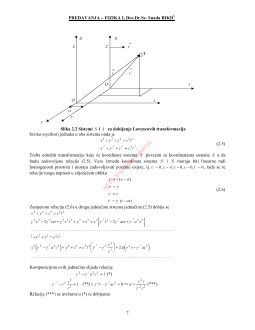
PREDAVANJA – FIZIKA I, Doc.Dr.Sc. Suada BIKI
Ć
z
z
→
T x
y z
( , , )
r
→
k
→
x
→
j
→
i
→
x
y
→
y
r
x y z
x i
y j z k
r
x
y
z
→
→ → →
→
→
→
= + + =
+
+
=
+
+
2
2
2
Slika 1.8 Radijus-vektor položaja ta
č
ke T u Kartezij-Dekartovom
pravouglom koordinatnom sistemu
2.
Me
đ
udjelovanje
Izgled sistema u kome se nalazimo je zasnovan na
č
etiri osnovna me
đ
udjelovanja. Sila je jedan od vektora
pomo
ć
u kojih se opisuje me
đ
udjelovanje. Ova dva vektora imaju isti pravac, intenzitet ali suprotan smjer.
Navedena
č
etiri tipa me
đ
udjelovanja su:
- gravitaciono
- elekromagnetsko
- jako nuklearno
- slabo nuklearno.
Karakteristika gravitacionog me
đ
udjelovanja je da ono ima isklju
č
ivo privla
č
ni karakter, konstanta
vezivanja je reda veli
č
ine
, dakle veoma je mala, a doseg me
đ
udjelovanja je beskona
č
an.
10
39
−
Elektromagnetsko me
đ
udjelovanje može biti privla
č
nog i odbojnog karaktera, a konstanta vezivanja
(odbijanja ) je reda
10
, što je znatno ve
ć
e od gravitacionog i doseg je beskona
č
an.
2
−
Jako nuklearno me
đ
udjelovanje je unutar jezgra ( nukleusa ) atoma koje vlada izme
đ
u nukleona
(
č
estice koje
č
ine jezgro ), konstanta vezivanja je reda veli
č
ine
10
, doseg je
10
( dimenzija atoma
je reda od
10
).
1
+
15
−
m
10
−
m
Slabo nuklearno me
đ
udjelovanje je locirano duboko unutar elementarnih
č
estica, doseg mu je nepoznat
ali je daleko manji od
10
, a konstanta vezivanja je reda od
10
.
15
−
m
12
−
Pod dosegom me
đ
udjelovanja se podrazumijeva ono mjesto u prostoru u kome je me
đ
udjelovanje
zanemarivo malo.
ZAKLJU
Č
AK
: Osnovni fenomen u prirodi je me
đ
udjelovanje koje se opisuje pomo
ć
u dva vektora koji
se nazivaju silama, a koji su istog pravca, istog intenziteta, a suprotnog smjera. Postojanje
me
đ
udjelovanja, odnosno njegovo opisivanje dvjema silama opisuje
III Njutnov
zakon
koji glasi: svaka
sila vezana je uz postojanje još jedne sile istog intenziteta, istog pravca, a suprotnog smjera (
zakon akcije
i reakcije
).
DEFINICIJA POLJA
: Posmatramo cijeli beskona
č
an prostor. Me
đ
utim, nas interesira samo dio
prostora u kome se osje
ć
a me
đ
udjelovanje. Taj dio prostora naziva se POLJE. Ako se neko tijelo kre
ć
e u
tom polju, onda ono me
đ
udjeluje sa tim poljem, dakle pod utjecajem te sile me
đ
udjelovanja (interakcije )
tijelo se kre
ć
e na odre
đ
eni na
č
in. Kada se tijelo na
đ
e u slobodnom prostoro ( dio prostora u kome se ne
4
NE RE
CENZIRANA S
K
RIPTA!
PREDAVANJA – FIZIKA I, Doc.Dr.Sc. Suada BIKI
Ć
osje
ć
a me
đ
udjelovanje ) ono se tada kre
ć
e brzinom stalnog intenziteta, po istom pravcu i u istom smjeru
(jednoliko pravolinijski ) ili pak miruje. To je
I Njutnov zakon
,
zakon inercije
.
POLJE
Tijelo se ne kre
ć
e
jednoliko
Slobodan dio prostora-Tijelo se kre
ć
e jednoliko pravolinijski
Tijelo se kre
ć
e jednoliko pravolinijski ili miruje kada se nalazi u takvom položaju u kojem je
me
đ
udjelovanje zanemarivo malo ili kada je suma svih vektora sila koje su rezultat me
đ
udjelovanja
jednaka nuli.
ZAKLJU
Č
AK : Ako nema me
đ
udjelovanja tijelo
ć
e se kretati jednoliko pravolinijski ili mirovati i
nastojati to stanje zadržati ( inertnost tijela). Veli
č
ina koja opisuje inertnost tijela naziva se MASA tijela.
Sistemi koji se kre
ć
u jednoliko pravolinijski ili miruju nemaju me
đ
udjelovanja pa kao posljedica jeste da u
takvim sistemima svi fizikalni zakoni imaju isti oblik, a takvi sistemi
se
nazivaju INERCIJALNI SISTEMI. Posmatra
č
koji se nalazi u inercijalnom sistemu nije u stanju da ocijeni
da li se kre
ć
e ili miruje ( nema me
đ
udjelovanja ), a posmatra
č
koji se nalazi u neinercijalnom sistemu u
stanju je da da dokaz o tome da se kre
ć
e jer osjeti silu tj. me
đ
udjelovanje.
2.1
Galilejeve transformacije
Posmatramo dva inercijalna sistema i
S
S
,
. Sistem miruje, a sistem
S
S
,
se jednoliko pravolinijski kre
ć
e
brzinom u smjeru ose
v
0
x
( Slika 2.1 ). U po
č
etnom momentu sistemi se poklapaju.
S
S
,
z
,
z
v
0
→
m
r
→
r
,
→
O
,
x
,
r
0
→
O
x
y
,
Slika 2.1 Sistemi i
y
S
S
,
za dobijanje Galilejevih transformacija
5
NE RE
CENZIRANA S
K
RIPTA!

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































