
Rotacija tačke, duži i trougla u prostoru
Prijava dokumenta
Napomena: Neke opcije za prijavu su dostupne samo nakon kupovine dokumenta.
1
Sadržaj
Sadržaj 1
UVOD
:Pojam rotacije 2
GLAVNI DIO
:Rotacija tačke u prostoru 4
Rotacija duži5
Rotacija trougla
8
Rotacija oko ose koja je u ravni projiciranja 9
Određivanje prave veličine duži rotacijom
9
ZAVRŠNI DIO
:Primjena rotacije 11
Izvori i literatura
13
Zapažanje mentora
14
2
UVOD:
Geometrijske figure i tijela se rotacijom oko nekog pravca (ose) dovode u nove,
općenitije položaje prema ravnima projekcija u kojima su jasnije prikazani radi lakšeg
rješavanja zadataka. Rotacija je okretanje tijela oko neke ose.
Prilikom rotacije sve tačke tijela opisuju kružne putanje sa središtem na nepomičnom
pravcu koji se naziva osa rotacije. Pri tome nije nužno da osa rotacije prolazi kroz
tijelo.
Rotacija je specifična po tome da prilikom „premještanja“ rotira objekt bez
deformacija, jer se svaka tačka rotira za isti ugao, tj rotacija je izometrijsko
preslikavanje. Riječ „izometrija“ je grčkog porijekla i u bukvalnom prevodu znači „ista
mjera“. To znači da se ovim preslikavanjem geometrijski lik preslikava u njemu
sukladan lik, dužina u njoj sukladnu đužinu, kružnica u njoj sukladnu kružicu, pravac
u pravac itd. Ovakvo preslikavanje čuva okomitost i paralelnost pravaca.
Rotacija u ravni vrši se repozicionirajući objekat duž kružne putanje za dati ugao u xy
ravni. U ovom slučaju rotiramo objekat oko osne tačke. Osna tačka je presječna
tačka ose rotacije koja je normalna na ravan xy i ravni xy.
Orijentisan ugao je onaj čiji kraci predstavljaju uređen par polupravih, tj zna se koji je
krak prvi, a koji drugi.
Pozitivno orijentisani ugao rotacije
je onaj koji je suprotan smjeru
kazaljke na satu.
4
Prilikom rotacije, obicno se zadaje da je osa rotacije okomita na jednu od
projekcionih ravnina π
1
ili π
2
ili da leži u jednoj od tih ravnina.
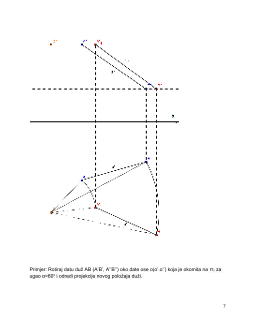
Data je tačka A sa svojim projekcijama, osa rotacije o okomita na π
1
i ugao rotacije
α(negativno orjentisan). Ravan Σ je ravan rotacije, postavljena je kroz tačku A i
paralelna je sa π
1
. (Σ II π
1
) Probodište ose rotacije sa ravni Σ je tačka O (O’). Duž OA
se naziva poluprečnik rotacije. Šestarom iz centra O sa poluprečnikom OA se opiše
luk kojem odgovara zadani ugao α. Dobijena tačka je rotirana tačka A, tj A
1
(A
1
’, A
1
’’).
Dužine OA, OA
1
,O’A’ i O’A
1
’ su jednake. OA=OA
1
=O’A’=O’A
1
’
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































