
Metoda sila
UNIVERITET U TRAVNIKU
FAKULTET ZA TEHNIČKE STUDIJE
GRAĐEVINA
STATIKA KONSTRUKCIJA 2
METODA SILA
Seminarski rad
Mentor: Prof.Dr Milorad Zrilić
Kandidat: Edin Mušija
Travnik, Februar, 2019.
2
OPĆENITO O STATIČKI NEODREĐENIM SISTEMIMA:
Sile u statički neodređenim sustavima (sistemima) ovise o broju i vrsti veza, te o omjeru
krutosti njegovih dijelova.
Uslijed prisilnih pomaka ili promjene temperature u sistemu pojavljuju se unutarnje sile i
sile reakcije. S obzirom da se pod djelovanjem sila sustav deformira, dolazi do iskrivljavanja osi
što znači da se javljaju i momenti na tim sistemima.
Promjena oblika dijela statički neodređenog sistema izazvati će promjenu i u ostalim
dijelovima sistema. Zamjenom zadanog opterećenja statički ekvivalentnim, doći će do promjene
sila na cijelom nosaču.
Statički neodređene sisteme moramo uvijek proračunavati kao jednu cjelinu tj., ne mogu
se izdvojiti pojedini elementi da bi se promatrali izdvojeno. Statički neodređeni sistemi (sustavi)
su oni sustavi kod kojih ne možemo odrediti unutarnje sile samo iz jednadžbi ravnoteže i to iz
razloga što imaju veći broj veza, te moramo uspostaviti onoliki broj jednadžbi koliko je i veza na
sistemu.
Za statički neodređen sistem kažemo da je to također sustav kod kojeg je broj veza veći
od minimalno potrebnog za geometrijsku nepromjenjivost. Takva definicija statički neodređenog
sustava naziva se kinematička definicija.
Da bi sistem bio u ravnoteži u ravnini, potrebno je postaviti tri (3) jednadžbe ravnoteže, a
najčešće se koriste jednadžbe: ΣM=0, ΣFx=0 i ΣFy=0. Prema tome, sistem (tijelo) će biti u
ravnoteži u ravnini samo ako je vektorski zbroj svih slia (i momenata) jednak nuli (nul-vektoru).
METODA SILA:
Metodom sila rješavamo statički neodređene sisteme zamišljenim raskidanjem veza pri čemu se
zadani sistem pretvara u statički određeni sistem, koji nazivamo osnovnim sistemom, a raskinute
se veze nadomještaju silama koje odgovaraju silama koje su te veze prenosile. Vrijednosti tih sila
potom izračunavamo iz uvjeta kompatibilnosti pomaka na mjestima raskinutih veza — sile
moraju povratiti narušenu neprekinutost polja pomaka ili osigurati podudaranje pomaka na
mjestima uklonjenih ležajeva sa stvarnim ležajnim uvjetima. Prilikom isključivanja sila na
sistemu mora se paziti da sistem ne pređe u mehanizam. Vrijednosti pomaka koji se pojavljuju u
4
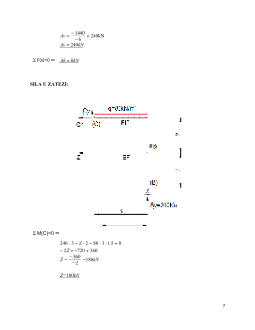
Zadatak :
Odrediti M dijagram pomoću metode sila?
q = 80 kN/m
,
(EI)
1
= 1,62 * 10
5
kNm
2
(EI)
2
= 1,944 * 10
5
kNm
2
EF = 2 * 10
6
kN
5
RJEŠENJE ZADATKA - METODA SILA - POTREBNO NACRTATI M DIJAGRAM ZA
SISTEM NA SLICI
Zadano: q=80kN/m', EI
1
=1,62x10
5
kNm
2
, EI
2
=1,94x10
5
kNm
2
, EI
1
=2,00x10
6
kNm
2
Određivanje statičke neodređenosti: zadani sustav u ravnini ima dva zgloba koji sprečavaju
horizontalne i vertikalne pomake, tj imaju ukupno 4 veze.
Da bi sustav u ravnini bio u ravnoteži, potrebno je minimalno tri veze, dakle 4-3=1.
Zadani sustav je statički 1 puta neodređen.
OSNOVNI sistem se dobiva zamišljenim isključivanjem jedne veze. Isključio sam vezu u točki
B, i omogućio horizontalni pomak. Naravno, mogao sam isključiti i vezu u točki A.
Sada određujem dijagram M0 na osnovnom sistemu od zadanog vanjskog opterećenja.
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































