Decibeli – istine i zablude

Zanat

Audio Engineer

Piše: Aleksandar Mikiæ

MUSIC • www.musicmagazin.co.yu

Decibel (dB) –
istine i zablude

Da li su svi decibeli isti? Koliko decibela je potrebno da se udvostruči nivo signala?
Brojni pokušaji su učinjeni kako bi se objasnio jedan od najkontroverznijih pojmova
audio i muzičke industrije. U kojoj meri je njihova primena značajna, saznajte više u
ovom nastavku.

ecibel (dB) je način da izrazimo
odnos između dve vrednosti
ili dva nivoa signala (u našem

slučaju), bez obaveze da navodimo
prave vrednosti ili nivoe. Na primer,
ako kažemo da izlaz iz pojačala daje
100 puta veću snagu od one koja je
izmerena na ulazu, onda je odnos izlaza
prema ulazu 100:1. Ovo nam i dalje ništa
ne govori o konkretnoj snazi pojačala –
to može da bude bilo koja količina volti
ili milivolti. Ali ako govorimo decibel
jezikom, onda kažemo da je izlaz +40dB
u odnosu na ulaz. Zašto je to baš 40dB?
Zato što ja tako kažem! Zato da bi
odstranili komplikovane kalkulacije iz
tonske režije. Kada govorimo o audio
sistemima i akustici, znajte da baratamo
ogromnim rasponom numeričkih
vrednosti. Najslabiji signal iz mikrofona
i najjači signal na izlazu iz pojačala,
pokrivaju raspon od preko hiljadu
miliona! U decibelima, taj raspon iznosi
podnošljivih 180dB što je, složićete
se, lakše za razumevanje. U stvari, kod
decibela u najgorem slučaju koristimo
trocifreni broj. I pošto je brojeva
manje, manja je i mogućnost greške.

Decibel i logaritmi

Ljudsko uvo operiše energetskim
rasponom od 10

:1(10,000,000,0

00,000:1). Pošto je ovakav raspon
ljudima teško razumljiv, usvojena je
logaritamska skala da bi se smanjile
mere na brojeve kojima se lakše
operiše. Logaritam (log) se uvećava
eksponencijalno, na sličan način kako

rade i naše uši kada je u pitanju utisak
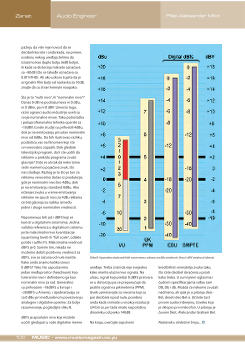
glasnosti. Zato decibeli i logaritmi
lepo funkcionišu zajedno, a rezultati
postaju jasni i praktični. (vidi sliku A).

Kako sam već napomenuo, decibeli se
često koriste za poređenje dva nivoa
signala – naveo sam primer ulaznih i
izlaznih nivoa pojačala. Ako je izlazni
nivo (Vizlaz) dvostruko veći od ulaznog
(Vulaz), onda je u pitanju pojačanje
od 6dB. Kalkulacija je sledeća:

Odnos u dB je: 20 x log(Vulaz/Vizlaz)

Ponekad međutim, umesto da
poredimo neke apstraktne vrednosti,
poželećemo da uporedimo nivo
signala sa deﬁnisanim referentnim
nivoom. Tada je, naravno, potrebno
da znamo šta taj nivo predstavlja i
kako se obeležava. Referentni nivo
označen je suﬁksom koji se dodaje
terminu dB, i podrazumeva vrlo
konkretnu vrednost. Najčešće korišćeni
dB termini jesu dBSPL, dBm, dBu, dBV
i dBFS, mada ih ima mnogo više.

dBSPL

koristimo kada hoćemo da

izrazimo nivo glasnosti. On označava
intenzitet zvučnog pritiska (SPL = Sound
Pressure Level). Referentna vrednost je
0 dBSPL, što je prag čujnosti. Pragom
čujnosti smatramo najtiši zvuk koji
je ljudsko uvo u stanju da registruje.
Nasuprot pragu čujnosti postoji i
prag bola, koji se označava sa 140
dBSPL. Iako to nije najglasniji zvuk koji
možemo da čujemo, iz ovoga možemo
da zaključimo da dBSPL raste kako
raste i nivo glasnosti. Kada čujete da
neko pomene decibele u kontekstu
nivoa buke, intenziteta, jačine zvuka,
glasnosti i sl, znajte da misli na dBSPL.
Kao ilustraciju, pogledajte tabelu 1, koja
prikazuje intenzitet zvučnog pritiska u
nekim situacijama, izražen u dBSPL.

tabela 1. Tipični dBSPL

primer

dBSPL

30m od mlaznog aviona

140

Prag (granica) bola

140

Prag (granica) nelagodnosi

120

Motorna testera, 1m udaljenosti

110

Diskoteka, 1m od zvučnika

100

Dizel kamion, 10m udaljenosti

Prometna saobraćajnica

Usisivač, 1m udaljenosti

Konverzacijski govor, 1m

Tipično kućno okruženje

Tiša biblioteka

Spavaća soba noću

TV studio, buka pozadine

List koji opada

Prag (granica) čujnosti

Zanat

mar-apr 2005

dBm

je stari referentni nivo za signale

u audio industriji, postavljen davnih
dvadesetih godina prošlog veka. Dobija
se kada se 1mW (1 milivat = 0,001
vat) električne snage propusti kroz
mrežno opterećenje od 600Ω(oma).
Poreklo je vezano za telekomunikacije
u Engleskoj iz tog vremena, ali to ovde
ne treba da nas zanima. Činjenica je,
međutim, da 1mW u 600Ω proizvodi
prosečan (rms) napon od 0,775
volti. 0 dBm je, znači, usvojen kao
standard čija referentna vrednost
iznosi 1mW, (‘m’ simbolizuje milivat).
Ali, dBm polako izlazi iz upotrebe.

dBu

- Srećom, praksa da se audio

veze opterećuju sa 600Ω napuštena
je u većem delu audio sveta, ali je
zato napon od 0,775 volti i dalje ostao
u upotrebi, samo sada kao nova

referentna vrednost. Kažem srećom,
zato što moderna audio tehnika poznaje
različite standarde kada je opterećenje
mreže u pitanju, tako da bi dBm danas
stvarao mnoge poteškoće u primeni,
mada je i dalje ponegde prisutan. Kada
govorimo o muzičkim instrumentima i
studijskim uređajima, današnja audio
industrija prihvatila je da se decibeli
vezuju za napon (u voltima) a ne za
snagu (u vatima). Da bi razlikovali stari
dBm (koji podrazumeva 600Ω) od
novog sistema, uveden je termin dBu
(‘u’ znači unterminated – neokončan,
i misli se na mrežu bez ﬁksnog
opterećenja). Tako dobijamo 0 dBu koji
predstavlja referentnih 0,775V (rms), bez
obzira na opterećenje mreže. Zato se
dBu odomaćio u studijskom okruženju
kao standard i danas se najčešće na
njega misli kada se pominju decibeli u

studiju. Još jednom podvlačim važnu
razliku između dBm i dBu: 0 dBu je uvek
0.775 volti, dok je 0 dBm uvek 1mW.

Ali čemu služe formule i kako nam
odnosi decibela mogu pomoći u
praksi? Jednostavno gledano, ako
se bavite muzikom ili snimanjem,
sigurno ste do sada primetili da
pojačavanje ili utišavanje, okretanje
dugmića na procesoru ili efektu,
povezivanje različitih audio uređaja
ili doterivanje akustike prostora,
uvek znače baratanje decibelima.
Praktično bavljenje decibelima
zahteva da znate o kojim decibelima
je reč, to jest, koju referentnu vrednost
decibel sa sobom nosi. U tu svrhu,
pogledajte primere referentnih
vrednosti i formula za izračunavanje
decibela koji su prikazani u tabeli 2.

Pogledajmo, na primer, šta se dešava
kada pojačate gitaru u snimku za
6dB, imajući u vidu da sada pričamo o
decibelima koji se odnose na napon
(dBu). Kalkulacija će nam reći da je
6dB dvostruko više od onoga što smo
prethodno imali. Znači li to da je gitara
sada duplo glasnija? Naravno da nije,
jer sada znamo da dBu i dBSPL nisu ista
stvar. Dodajući 6dB mi udvostručujemo
ono što pokazuju pikmetri (makar oni
prikazivali i dBSPL), ali ako hoćemo
da udvostručimo subjektivni utisak
glasnosti, onda moramo da pojačamo
izvor za 10dB. Pogledajmo šta se dešava
kada podignemo regler na mikseti
za 10dB? Tada će i napon na izlazu iz
miksete, i snaga na izlazu iz pojačala, i
SPL ispred zvučnika izmeriti uvećanje
od 10dB. Međutim, numerički gledano,
dok su napon i SPL uvećani za 3,16

puta, snaga (u vatima) se povećala za
(3,16)

, što je deset puta! Otkuda ta

razlika? Evo zlatnog pravila koje treba
da zapamtite: udvostručavanje snage
(u vatima) iznosi 3dB, udvostručavanje
napona (u voltima) iznosi 6dB, dok
udvostručavanje jačine zvuka (u SPL)
iznosi 10dB. Biće vam lakše ako naučite
da se služite formulama koje deﬁnišu
međusobni odnos decibela, kao i
decibela i drugih veličina, (vidi tabelu 3).

Koliko dB je pojačalo od 40 vati? To
zavisi od toga šta smo u njega uključili.
Ali znamo da je pojačalo koje na izlazu
daje 40dB, predviđeno da ulazni signal
pojača 100 puta! Zar nije logičniji
ovakav način izražavanja? Možda još
nije, ali to je verovatno zato što, iz
iskustva, već imate neku predstavu
o tome koliko je glasno pojačalo od
40 vati. Ali ako nemate to iskustvo,
sigurno vam koristi da zapamtite da
treba da podignete regler za 10dB na
mikseti kako bi učinili zvuk dvostruko
glasnijim, ili da podizanje reglera za
20dB desetostruko pojačava originalnu
informaciju. S druge strane, malo vam
znači ako vam kažem da pojačate zvuk
za 40 vati jer, koliko je 40 vati zapravo
glasnije? Nije jasno zato što ne znamo
u odnosu na koju drugu vrednost je to
glasnije. Zato je korisno da razmišljate
i da se izražavate u decibelima.