
Elasticne linije Pregled
Izvo
đ
enje diferencijalne jedna
č
ine elasti
č
ne linije
elasti
č
na linija kod proste grede
elasti
č
na linija kod konzole
Elasti
č
na linija,
č
ija je jedna
č
ina y(z), je krivolinijski oblik ose nosa
č
a izazvan
optere
ć
enjem. Koordinatni sistem
ć
emo uvek uzimati tako da je koordinatni
po
č
etak na levom kraju nosa
č
a, gde je osa z usmerena u desnu stranu a osa y
naniže. Za svako z se zna y (ugib) i
α
(ugao nagiba, nagib). Precizno re
č
eno
,
tan
y
′
=
α
me
đ
utim pošto se radi o malim deformacijama i y‘ se smatra malom
veli
č
inom, imamo da je zbog
č
ega prakti
č
no važi da je
To zna
č
i da se ugao nagiba (nagib) na ma kom mestu nosa
č
a, ozna
č
en sa
α
,
β
ili
druga
č
ije, odre
đ
uje preko prvog izvoda jedna
č
ine elasti
č
ne linije.
Jedna
č
ine elasti
č
nih linija, u elementarnim slu
č
ajevima proste grede i konzole,
dobijene su nakon integracija diferencijalne jedna
č
ine elasti
č
ne linije gde se
integracione konstante dobijaju iz grani
č
nih uslova.
( )
( )
.
z
y
z
′
=
α
,
tan
α
≈
α
Grani
č
ni uslovi za prostu gredu su: y(0)=0 i y(l)=0, a za konzolu: y(0)=0 i y'(0)=0.
Dakle, na mestu oslonaca ugibi su jednaki nuli a na mestu uklještenja i ugib i nagib.
Za izvo
đ
enje diferencijalne jedna
č
ine
elasti
č
ne linije polazi se od ranije
dobijene relacije koja povezuje njen
polupre
č
nik krivine
ρ
i veli
č
ine E, I
x
i
M:
⇒
=
ρ
x
I
M
E
S obzirom da je za male deforma-
cije poznata formula iz
diferencijalne geometrije za polu-
pre
č
nik krivine
( )
,
0
2
≈
′
y
( )
[
]
,
1
2
3
2
y
y
′′
′
+
=
ρ
daje
⇒
′′
=
ρ
y
1
( )
2
.....
1
y
′′
=
ρ
( )
1
.....
1
x
EI
M
=
ρ
Na osnovu jednakosti (1) i (2) i
č
injenice da je, prema usvojenoj konvenciji o
znaku momenta savijanja i smeru ose y, moment pozitivan kada je drugi izvod
funkcije y po z negativan, diferencijalna jedna
č
ina elasti
č
ne linije ima oblik:
( )
3
.....
x
EI
M
y
−
=
′′
( )
⇒
=
z
M
M
( )
.
z
y
y
′′
=
′′
U slu
č
ajevima koje
ć
emo prou
č
avati važi
ć
e da je
.,
const
EI
x
=
( )
( )
⇒
−
=
′
=
′′
−
=
′′
2
2
2
,
,
z
q
z
ql
z
M
dz
y
d
y
EI
z
M
y
x
Elasti
č
na linija za prostu gredu optere
ć
enu
ravnomernim kontinualnim optere
ć
enjem:
⇒
−
−
=
′
dz
z
q
z
ql
EI
y
d
x
2
2
2
1
⇒
+
−
−
=
′
∫
1
2
2
2
1
C
dz
z
q
z
ql
EI
y
x
Deformacije izazvane uticajem više optere
ć
enja
jednake su algebarskom zbiru deformacija svakog
optere
ć
enja posebno.
Kona
č
ni oblik jedna
č
ine elasti
č
ne u tablicama je dat u obliku:
=
y
( )
z
y
y
1
=
( )
,
z
g
+
( )
z
y
1
sa zna
č
enjem
i
0
za
a
z
≤
≤
( ) ( )
( )
z
y
z
g
z
y
y
2
1
=
+
=
.
za
b
a
z
a
+
≤
≤
Superponiranje deformacija.
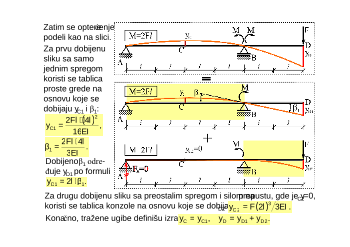
Primer 4.1 Za prostu gredu prikazanu na slici
odrediti uglove nagiba kod oslonaca i ugib sredine?
,
3
2
1
α
−
α
+
α
=
α
,
3
2
1
β
−
β
+
β
=
β
.
3
2
1
y
y
y
y
−
+
=
( )
( )
,
384
2
5
,
24
2
4
1
3
1
1
EI
l
q
y
EI
l
q
=
=
β
=
α
( )
( )
,
48
2
,
16
2
3
2
2
2
2
EI
l
F
y
EI
l
F
=
=
β
=
α
( )
( )
( )
.
16
2
,
3
2
,
6
2
2
3
3
3
EI
l
M
y
EI
l
M
EI
l
M
=
=
β
=
α
Na osnovu tablica, potrebni ugibi i nagibi za
pojedina
č
na optere
ć
enja imaju vrednosti:
Na osnovu principa superponiranja deformacija
tražene deformacije (ugib i nagibe) definišu izrazi:
Primer 4.2 Za konzolu prikazanu na slici
odrediti ugibe na mestima C i B i nagib kraja?
Na osnovu principa superponiranja deformacija
tražene deformacije (ugibe i nagib) definišu
izrazi:
Na osnovu tablica, potrebni ugibi i nagibi za
pojedina
č
na optere
ć
enja imaju vrednosti:
.
,
3
2
1
3
2
1
B
B
B
B
C
C
C
C
y
y
y
y
y
y
y
y
−
+
=
−
+
=
,
3
2
.
1
β
−
β
+
β
=
β
( )
,
2
2
4
6
2
24
2
2
2
4
1
+
−
=
l
l
l
l
l
l
EI
l
q
y
C
( )
,
8
2
4
1
EI
l
q
y
B
=
( )
,
6
2
3
1
EI
l
q
=
β
,
3
3
2
EI
Pl
y
C
=
,
2
2
2
EI
Pl
=
α
=
β
( )
,
2
3
2
6
2
2
3
3
−
=
l
l
l
l
EI
l
F
y
C
( )
.
3
2
3
3
EI
l
F
y
B
=
,
2
2
α
+
=
l
y
y
C
B
( )
,
2
2
2
3
EI
l
F
=
β
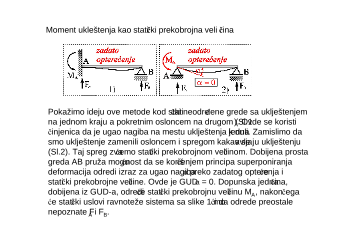
Želiš da pročitaš svih 21 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































