studenti.rs home page

                     

                      ШКОЛА МАТЕМАТИКЕ И РАЧУНАРА РАЈАК     

                      

www.rajak.rs

 

1 

 

Површина и запремина пирамиде

 

Пирамида је полиедар који има n+1 страну од којих је једна n-тоугао ( многоугао ) и  

n троуглова. 

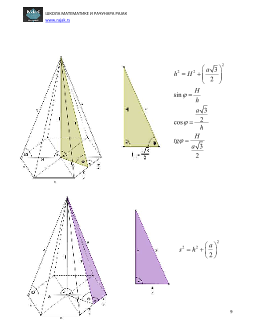
A,B,C,D,E,F – темена основе 

S – врх пирамиде 

ABCDEF – основа ( база ) пирамиде 

AB,BC,CD,DE,EF,FA – ивице основе 

SA,SB,SC,SD,SE,SF – бочне ивице 

ABS,BCS,CDS,DES,EFS,FAS – бочне стране 

H – висина пирамиде       

h – апотема ( висина бочне стране ) 

FDS – један дијагонални пресек пирамиде 

 

 

Основа пирамиде је n-тоугао ( многоугао ), а бочне стране ( троуглови ) чине 

омотач пирамиде. 

Пирамида је права ако су јој све бочне ивице једнаке и ако се око њене основе 

може описати круг чији је центар у подножју висине пирамиде. 

Висина пирамиде је дуж која спаја врх пирамиде и његову нормалну пројекцију на 

раван основе. 

 

 

 

                     

                      ШКОЛА МАТЕМАТИКЕ И РАЧУНАРА РАЈАК     

                      

www.rajak.rs

 

2 

 

 

 

 

 

 

 

 

 

Висина бочне стране ( апотема ) је дуж која из врха пирамиде пада нормално на 

основну ивицу пирамиде. 

Дијагонални пресек пирамиде је пресек пирамиде који садржи две несуседне 

бочне ивице пирамиде. 

 

 

Правилна пирамида у основи има правилан многоугао, једнакостраничан троугао, 

квадрат, правилан шестоугао... 

 

 

background image

Želiš da pročitaš svih 9 strana?

Prijavi se i preuzmi ceo dokument.

Registruj se besplatno Pošalji dokument

Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.