
Funkcije: seminarski rad iz inženjerske matematike Pregled
Seminarski rad iz predmeta Inženjerska matematika Milan Paunović EPO 19/12
1
SEMINARSKI RAD
FUNKCIJE
Visoka škola elektrotehnike i računarstva
strukovnih studija u Beogradu
Student:
Milan Paunović EPO – 19/12
Profesor:
dr Ana Savić
Predmet:
Inženjerska matematika
Seminarski rad iz predmeta Inženjerska matematika Milan Paunović EPO 19/12
2
SADRŽAJ:
1.POJAM FUNKCIJE……………………….…………………..…………2
1.1 PROMENLJIVE VELIČINE………………………………….……..…...2
1.2 FUNKCIJA (PRESLIKAVANJE)...…..……………………………..…...2
1.3 NAČINI IZRAŽAVANJA FUNKCIJE……….……………………..…...5
2. NEKA SVOJSTVA FUNKCIJA……..…….……..………………..…...6
3. INVERZNA FUNKCIJA…………....……….……………………..…...9
4. KLASIFIKACIJA ELEMENTARNIH FUNKCIJA…………….…...10
4.1 RACIONALNE FUNKCIJE………………….………………........…...10
4.2 ALGEBARSKE FUNKCIJE………………….………………........…...11
4.3 TRIGONOMETRIJSKE FUNKCIJE……...….…………………....…...12
4.4 LOGARITAMSKA I EKSPONENCIJALNA FUNKCIJA………..…...14
4.5 INVERZNE TRIGONOMETRIJSKE FUNKCIJE…………..….....…...15
5. NEPREKIDNOST FUNKCIJE. GRANIČNA VREDNOST
FUNKCIJE…………………………………………………………………16
5.1 NEPREKIDNOST FUNKCIJE U TAČKI………..…………..….....…...16
5.2 FUNKCIJA PREKIDNA U TAČKI………..……….………..….....…...18
5.3 GRANIČNA VREDNOST FUNKCIJE...…..……….………..….....…...18
5.4 GRANIČNA VREDNOST I NEPREKIDNOST….………..…........…...19
5.5 LEVA I DESNA GRANIČNA VREDOST FUNKCIJE…...…........…...19
LITERATURA…………………………………………………………….20
Seminarski rad iz predmeta Inženjerska matematika Milan Paunović EPO 19/12
4
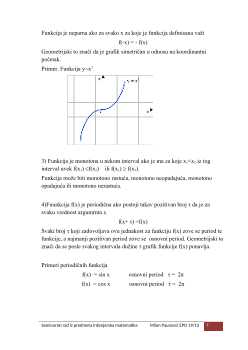
Iz relacije:
y=√(1-x
2
) (1)
gde je aritmetički koren na desnoj strani realan za
-1 ≤ x ≤ 1, (2)
dobijaju se sve odgovarajuće vrednosti y:
0 ≤ y ≤ 1. (3)
Obratno, svakom realnom broju y koji zadovoljava nejednakosti (3) odgovara
bar po jedan realan broj x kojizadovoljava nejednakosti (2).
Kada je nekom formulom zadato preslikavanje skupa brojeva x koji
zadovoljavaju nejednakosti (2) na skup brojeva y koji zadovoljavaju uslov
(3). To preslikavanje može se označiti ovako:
f : x→√(1-x
2
)
ili pošto se zna zakon korespodencije samo
x→√(1-x
2
)
Umesto preslikavanja kaže se funkcija pa se piše
x→f(x) gde je f(x) =√(1-x
2
)
ili kratko
f(x) =√(1-x
2
).
Skup svih realnih brojeva x koji se preslikavaju obeleđavamo sa E. Taj skup
se zove oblast definisanosti funkcije. Skup svih realnih brojeva y na koje se
preslikavaju elementi x obeleđavaćemo sa F. Taj skup se zove oblast
vrednosti funkcije. Skup E i F nemoraju biti podskupovi skupa prirodnih
brojeva. Kad je E skup elemenata ma koje prirode, a F je odgovarajući skup
elemenata.
Funkcija je zakon po kome se svakom elementu x iz skupa E dodeljuje jedan
element y iz skupa F.
Dirihleova definicija funkcije
Seminarski rad iz predmeta Inženjerska matematika Milan Paunović EPO 19/12
5
Promenljiva veličina y zove se funkcija nezavisno promenčljive veličine x
koja pripada skupu E ako svakoj vrednosti veličine x € E odgovara po
izvesnom zakinu uvek samo po jedna odredjena vrednost veličine y.
To pišemo
z = f(x).
1.3 NAČINI IZRAŽAVANJA FUNKCIJE
1)Tablično.
x
x
1
x
2
x
3
x
4
x
5
x
6
x
7
y
y
1
y
2
y
3
y
4
y
5
y
6
y
7
2)Analitički način zadavanja funkcije
Sastoji se uizrađavanju funkcije odgovarajućim analitičkim izrazom.
y=x
2
+ 2x – 3
y=sin x
y=tg x
y=(log x – 2
x
) / 2
3) Grafički način izrađavanja funkcije u očiglednom geometrijskom
predstavljanju funkcije u nekom koordinatnom sistemu.

Želiš da pročitaš svih 20 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































