Вјежба број
_____1_____
Страна
____1_____
Студент:
___________________________________________
ВJEЖБУ
OВJEPИO(-ЛA):
ДATУM
ПРЕДАЈЕ
ВЈЕЖБЕ
:
Јун 2014
Eлаборат бјежби из предмета
Геодезија
Државни координатни систем Републике Српске
(објаснити Гаус-Кригерову пројекцију). Размјера
Да би се земљина површ приказала на карти , мора се извршити њено
пресликаванје на раван или неку другу површ која се може развити у раван
(конус или цилиндар). Површ земље (геоид, тј. елипсоид) није могуће
развити у раван без деформације , односно тачке које се налазе на елипсоиду
не могу се пренијети у раван, а да при томе не дође до промјене растојања
између тачака. Деформацијама подлијежу углови, дужине и површине.
Република Српска , као и већина европских земаља, усвојила је
Гаус-
Кригерову пројекцију.
Ова пројекција је добила име по њемачком геодету
Карл Фридрих Гаусу, коју је он први пут употријебио за премјеравање града
Хановера. Замијенио је геоид елипсоидом, а не како је до тада рађено
лоптом. Послије његове смрти Гаусову пројекцију усавршио је Кригер који
је дао основне једначине за прелаз са елипсоида на раван.
Код Гаус-Кригерове пројекције, као пројекцијска површ, користи се
цилиндар (омотач ваљка), у који је смјештен елипсоид тако да оса цилиндра
лежи у равни еквадора. Цилиндар додирује елипсоид по једном меридијану –
додирном меридијану. Додирни меридијан пресликава се на цилиндар без
деформације, тј. његова дужина је иста као на елипсоиду, док су све остале
дужине ван додирног меридијана деформисане и немају исту вриједност на
елипсоиду као на пројекцијској равни. Такође треба напоменути да су
деформације веће што се више удаљава од додирног меридијана. Води се
рачуна да максимална деформација дужина износи 1
dm
на дужино од 1
km.
Вjeжбa бp.:
___1___
_
Стpaницa бр.:
___
2
___
Студент:
__________________________________________
ВJEЖБУ
OВJEPИO(-ЛA):
ДATУM
ПРЕДАЈЕ
ВЈЕЖБЕ:
Јун 2014.
Eлаборат бјежби из предмета
Геодезија
Подручије бивше СФРЈ приказано је у облику тростепених меридијанских
зона и то су: 5, 6, 7 зона, гдје почетак координатног система чине пресјек 15,
18, 21 меридијана са равни еквадора. Такође, битно је нагласити да бројеве
координатних система добијамо када се географске дужине додирних
меридијана подијеле са ширином зоне 3˚ (15:3=5; 18:3=6; 21:3=7).
Елипсоид се пресликава на цилиндар по следећим условима:
Оса цилиндра лежи у равни еквадора
Пројекција мора бити конформна ( сачувана је сличност облика слика)
Средњи меридијан се пресликава као права линија, његова пројекција
представља X-осу координатног система у равни, а цијела пројекција у
односу на њу је симетрична
Сваки дио X-осе мора бити једнак или стајати у константном односу
према одговарајућем луку меридијана.
Кад се цилиндар расијече по изводници па се развије у раван, добија се
изглед пресликаоног дијела Земље. Код ове пројекције, меридијани и
паралеле се пресликавају као управне линије. Додирни меридијан и еквадор
се пресликавају као праве међусобно управне линије, док си остали
меридијани симетрични у односу на додирни меридијан, а паралелне у
односу на екватор.
У координатном систему, положај сваке тачке одређен је правоуглим
координатама X и Y. Како је цијели простор бивше Југославије на сјеверној
страни полулопте, све тачке имају позитивне вриједности X. Вриједности Y
биле би за тачке источно од додирног меридијана позитивне, а западно
негативне.
Да се не би рачунало са негативним координатама, што би отежало рачун, X-
оси се даје вриједност Y=500 000 m. Тако ће све тачке источно од додирног
меридијана имати Y веће од 500 000 m, а тачке западно од додирног
меридијана имаће Y мање од 500 000 m.
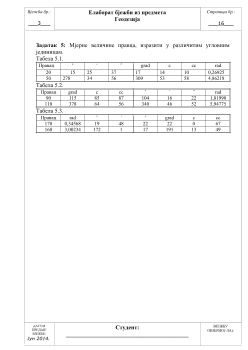
Задатак 1.
Описати положај Тачке М (Y=6 467 001.30 m ; X=4 781 864.67 m)?
Из координата тачке М (Y ; X) можемо закључити следеће:
- на основу броја 6 у вриједности Y координате закључујемо да се
тачка М налази у 6-ој зони (територија бивше Југославије)
- број 467 001.30 m је мањи од броја 500 000 m па закључујемо да се
тачка М налази западно од средњег меридијана 6-е зоне
- на основу разлике бројева 500 000 m и броја 467 001.30 m која
износи 32 998.07 m закључујемо да је тачка удаљена управо 32
998.07 метара од средњег меридијана
- вриједност X координате нам говори да се тачка М налази сјеверно
од ек
Вjeжбa бp.:
___1___
_
Студент:
__________________________________________
ВJEЖБУ
OВJEPИO(-ЛA):
ДATУM
ПРЕДАЈЕ
ВЈЕЖБЕ:
Јун 2014.
Eлаборат бјежби из предмета
Задатак 2.
Ако је на терену измјерена дужина од 173 m, колика је њена
дужина у дециметрима на катастарском плану размјере 1:5000?
173
m
5000
=
0,0316
m
=
0,346
dm
Задатак 3.
Ако је на топографској карти размјере 1:10 000 измјерена дужина
од 173 cm, колика је њена дужина у метрима у природи?
173×10000=
1730000 m
Задатак 4.
Одредити размјеру дате топографске подлоге (дате у прилогу 1).
Tačka
Y(m)
X(m)
23
6 415 643.43 4 813 207.20
29
6 415 306.25 4 813 310.03
25
6 415 585.50 4 813 409.80
Размјера дате топографске подлоге износи 1:2000
Стpaницa бр.:
___
4
___
Вjeжбa бp.:
___2___
_
Стpaницa бр.:
___
5
___
Студент:
___________________________________________
ВJEЖБУ
OВJEPИO(-ЛA):
ДATУM
ПРЕДАЈЕ
ВЈЕЖБЕ:
Јун 2014.
Eлаборат бјежби из предмета
Геодезија
Мјерило угла. Мјерило дужине. Мјерило висинске разлике.
Мјерило угла – теодолит
За угао постоји више дефиниција, а различите струке користе оне
дефиниције које им највише одговарају. У суштини угао је дио равни
ограничен двјема полуправим које се сијеку у једној тачки. Дио равни
између полуправих назива се област угла, полуправе називамо крацима угла
а пресјечна тачка представља тјеме угла. У геодезији се одређује вриједност
угла, која представља мјеру обртања за колико треба ротирати лијеви крак
угла у смијеру кретања казаљке на часовнику да поклопи десни крак угла. За
разлику од математике, позитивни смијер обртања у геодезији усвојен је да
се поклапа са смијером кретања казаљке на часовнику, односно обрнуто него
у математици.
Углови у хоризонталној равни називају се хоризонтални, док се у
вертикалној равни могу мјерити вертикални углови или зенитски углови,
који се често називају зенитска растојања. Угломјери намијењени за мјерење
хоризонталних углова и зенитских углова имају подјелу нанијету супротно
кретању казаљке на часовнику. Уобичајно је да се за означавање
хоризонталних углова користи ознака β а вертикалне α а зенитна растојања
Z. Да би се извршило одређивање неког угла у природи потребно је имати
одговарајући прибор за мјерење углова. Као основни дио тога јесте
инструмент назван
Теодолит.
Вjeжбa бp.:
___2___
_
Стpaницa бр.:
___
7
___
Студент:
__________________________________________
ВJEЖБУ
OВJEPИO(-ЛA):
ДATУM
ПРЕДАЈЕ
ВЈЕЖБЕ:
Јун 2014.
Eлаборат бјежби из предмета
Геодезија
алхидадина оса.
Дурбин је, заједно са вертикалним лимбом, чврсто везан за обртну освину
дурбина, која се крајевима ослања на носаче дурбина. На тај начин
омогућена је ротација дурбина у вертикалној равни управној на обртну
осовину дурбина. Уколико обртна осовина дурбина није хоризонтална,
дурбин се неће окретати у вертикалној него некој нагнутој равни.
Пошто се алхидада хоризонталног лимба може окретати хоризонтално око
своје осе, а дурбин око обртне осе вертикално, то се он може усмјерити у
правцу ма које тачке, коју је потребно опажати.
За прецизно очитавање подјеле на лимбу теодолит је снадбјевен
специјалним направама, ткз.лупама са нонијусима или микроскопима.
Приликом опажања правца теодолит се поставља на статив који на горњем
дијелу има равну плочу (главу статива). Статив служи као постоље на које се
поставља теодолит, а висина теодолита се подешава тако да се опазач осјећа
угодно приликом мјерења углова. Помоћу централног завртња (16), се
инструмент повезује са стативом.
Теодолит се код старијих конструкција фиксирао за статив помоћу
спиралног пера (опруге), а касније је спирално перо замијењено еластичном
плочицом.
Да би центар лимба био тачно на истој вертикали која пролази кроз тјеме
углова служимо се направом која се назива висак.
