UNIVERZITET U ISTOČNOM SARAJEVU
SAOBRAĆAJNI FAKULTET
DOBOJ
INŽENJERSKA GRAFIKA
1. PITANJA IZ NACRTNE GEOMETRIJE
01. Koje tačke pravca zovemo 1. 2. i 3. probodište pravca?
Probodište pravca nazivamo tačku u kojoj pravac probada ravninu
- PRVO PROBODIŠTE pravca je tačka u kojoj pravac probada horizontalnu ravninu π
1
- DRUGO PROBODIŠTE pravca je tačka u kojoj pravac probada vertikalnu ravninu π
2
- TRECE PROBODIŠTE pravca je tačka u kojoj pravac probada vertikalnu ravninu π
3
02. Koji ugao zovemo 1. 2. i 3. prikloni ugao pravca?
PRVI
PRIKLONI UGAO PRAVCA (α
1
) je ugao između pravca i ravni π
1,
odnosno to je ugao između pravca i
njegovog tlocrta
DRUGI
PRIKLONI UGAO PRAVCA (α
2
) je ugao između pravca i ravni π
2,
odnosno to je ugao između pravca i
njegovog nacrta
TRECI
PRIKLONI UGAO PRAVCA (α
3
) je ugao između pravca i ravni π
3,
odnosno to je ugao između pravca i
njegovog bokocrta
03. Koje pravce ravni nazivamo tragovi ravni i koliko ih ima?
Trag je pravac u kojem ravnina sječe horizontalni ili vertikalnu ravninu (π
1,
π
2
ili π
3
) postoje tri traga ravni.
04. Koju ravninu nazivamo 1. projicirajuda? Gdje se elementi te ravni (tačke, pravci, dužine, likovi…) projiciraju
u tlocrtu?
PRVA PROJICIRAJUDA RAVNINA je ona okomita na π
1
i sve što leži u njoj, ima svoj tlocrt u prvom tragu
05. Koju ravninu nazivamo 2. projicirajuda? Gdje se elementi te ravni (tačke, pravci, dužine, likovi…) projiciraju
u nacrtu?
DRUGA PROJICIRAJUDA RAVNINA je ona okomita na π
2
i sve što leži u njoj, ima nacrt u drugom tragu
06. Koju ravninu nazivamo 3. projicirajuda? Gdje se elementi te ravni (tačke, pravci, dužine, likovi…) projiciraju
u bokocrtu?
TREDA PROJICIRAJUDA RAVNINA je ona okomita na π
3
i sve što leži u njoj, ima bokocrt u tredem tragu
07. Koje pravce ravni nazivamo sutražnice 1. skupine?
Prvi glavni pravci ravni, ili sutražnice 1. skupine su pravci paralelni s π
1
, tj. paralelni s 1. tragom ravni, koji
probadaju π
2
08. Koje pravce ravni nazivamo sutražnice 2. skupine?
Drugi glavni pravci ravni, ili sutražnice 2. skupine su pravci paralelni s π
2
, tj. paralelni s 2. tragom ravni, koji
probadaju π
1
09. Koje pravce ravni nazivamo sutražnice 3. skupine?
Tredi glavni pravci ravni, ili sutražnice 3. skupine su pravci ravni paralelni s tredim tragom te ravni
10. Čime je određena ravnina?
Ravnina je određena svojim tragovima
11. Kako se zove pravac duž kojeg se sijeku dvije ravni? Koji je to pravac ako su ravni paralelne?
Pravac duž kojeg se sijeku dvije ravni zove se presječnica. Ako su ravni paralelne, presječnice nema jer se ne
ravni ne sijeku
12. Koje pravce ravni zovemo priklonice 1. skupine?
Priklonica 1. skupine je svaki pravac ravni, koji s 1. tragom zatvara pravi ugao
13. Koje pravce ravni zovemo priklonice 2. skupine?
Priklonica 2. skupine je svaki pravac ravni, koji s 2. tragom zatvara pravi ugao
14. Koje pravce ravni zovemo priklonice 3. skupine?
Priklonice 3 skupine je svaki pravac ravni okomiti na 3. trag te ravni
15. Kada pravac leži u ravnini?
Pravac leži u ravnini kada su mu minimalno dvije tačke elementi te ravni
16. Šta mora biti ispunjeno ako pravac leži u ravnini?
Pravac leži u ravnini kada su mu minimalno dvije tačke elementi te ravni
17. Kada je ravnina paralelna s nekim pravcem u prostoru?
Ravnina je paralelna s nekim pravcem u prostoru kada je projekcija tog pravca na tu ravninu, prava veličina
18. Kada je pravac okomit na ravninu?
Pravac je okomit na ravninu kada je njegova projekcija na tu ravninu tačka
19. Ako je pravac okomit na ravninu, kako se to odražava u projekcijama?
U jednoj i drugoj projekciji pravac je okomit na trag
20. Kada je ravnina okomita na ravninu?
Ravnina je okomita na ravninu ako sadrži barem jedan pravac okomit na tu ravninu
21. Da li se čuva okomitost pravca kod ortogonalnog projiciranja?
Da, ako je pravac okomit na ravninu, njegov tlocrt je okomit na 1.trag,a njegov nacrt na 2.trag te ravni
22. Kada tačka leži u ravnini?
Tačka leži u kada lezi na sutražnici te ravni
23. Koji ugao zovemo 1. prikloni ugao ravni?
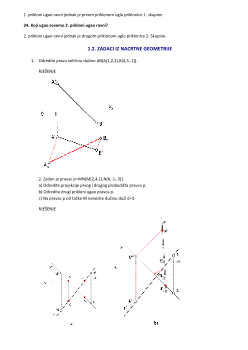
3. Odredite tlocrt tačke B(2,-,3), ako ona leži u ravni P(5,3,∞). Kako nazivamo ravan P? Zašto?
RJEŠENJE
4. Odredite nacrt tačke A(2,3,-), ako ona leži u ravni P(4,∞,2).
Kako nazivamo ravan P? Zašto?
RJEŠENJE
5. Tačka M leži u ravni Σ kojoj je pravac s1 prvi trag. Konstruišite drugi trag ravni Σ.
RJEŠENJE
6. Tačka M leži u ravni Ρ kojoj je pravac r2 drugi trag. Konstruišite prvi trag ravni P.
RJEŠENJE
9. Tačka T(2,1,-) leži u ravni Σ(5,3,5). Konstruišite nacrt tačke T pomodu njezine priklonice 1. skupine.
RJEŠENJE
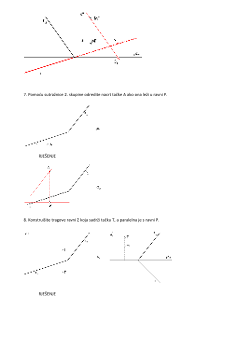
10. Odredite 1. i 2. prikloni ugao ravni Σ(-3,2,-5).
RJEŠENJE
11. Pravac p=P1P2[P1(0,-2,0),P2(3,0,2)] je priklonica 2. skupine ravni P. Konstruišite tragove ravni P.
RJEŠENJE
