Predmet : Matematika
Tema : Kompleksni brojevi
SEMINARSKI RAD
Mentor: Doc. Dr. Sead Rešić Student: Sanja Štrbac
Asistent : Mr. Selmir Dadanović
Broj indeksa: S- 26/12 - I
UVOD
Imaginarni brojevi prvi put su se pojavili u 16. stoljeću vezano za problem rješavanja
kubne jednadžbe. Njihova upotreba raširila se tokom 19. stoljeća, kad su se pojavile i
prve primjene.
Kompleksni brojevi
se definiraju kao sve linearne kombinacije
1
(s realnim koefcijentima)
brojeva 1 i i tj. kompleksni brojevi su brojevi oblika z = x + yi s x; y 2 R. Broj x se zove
realni dio, a broj y imaginarni dio
kompleksnog broja z (dakle: i realni i imaginarni dio
kompleksnog broja su realni brojevi).
Početkom 19. stoljeća Argand i Gauss uveli su način vizualizacije kompleksnih brojeva.
Svaki kompleksan broj z = x + yi možemo poistovjetiti s točkom (x; y) u koordinatnoj
ravnini (I obrnuto: svakoj točki odgovara kompleksan broj), uz uobičajeni Cartesiusov
koordinatni sustav.
1
Linearne kombinacije su izrazi oblika fx + fy + : : :, gdje su f; f; : : : skalari, a x; y; : : : vektori.
1
1.
Kompleksni brojevi
Imaginarni brojevi prvi put su se pojavili u 16. stoljeću vezano za problem rješavanja
kubne jednadžbe. Njihova upotreba raširila se tokom 19. stoljeća, kad su se pojavile i
prve primjene.
Najpoznatije primjene vezane su za teoriju elektriciteta i magnetizma (koju bitno
pojednostavljuju) te za kvantnu teoriju.
Kao motivacija za uvođenje imaginarnih brojeva obično se uzimaju kvadratne jednadžbe
s realnim koefcijentima. Poznato je da ako je diskriminanta D = b
2
- 4ac kvadratne
jednadžbe ax
2
+bx+c = 0 negativna, ta jednadžba nema realnih rješenja. Osnovni primjer
takve jednadžbe je
x
2
+ 1 = 0:
Po dogovoru, ta jednadžba (iako nema realnih rješenja jer bi to bio realan x koji kvadriran
daje negativan broj -1) ima dva rješenja u kompleksnim brojevima. To su
2
i
i -i
tj. Oba
broja (
i
i
-i
) su rješenja kvadratne jednadžbe x
2
+1 = 0 (kao što su 1 i -1 rješenja kvadratne
jednadžbe x
2
-1 = 0). Broj
i
zove se imaginarna jedinica. Dakle, defnicija imaginarne
jedinice je da je to jedan od dva moguća broja koji kvadrirani daju 1:
i
2
= -1:
Isto svojstvo ima
i -i
: (-i)
2
=
(-i)(-i)
= (-1)
2
i
2
= 1 f (-1) = -1.
Kompleksni brojevi
se definiraju kao sve linearne kombinacije
3
(s realnim koefcijentima)
brojeva 1 i i tj. kompleksni brojevi su brojevi oblika
z = x + yi
s x; y 2 R. Broj x se zove realni dio, a broj y imaginarni dio
kompleksnog broja z (dakle: i
realni i imaginarni dio kompleksnog broja su realni brojevi). Skup svih kompleksnih
brojeva označavamo s C. Skup R je podskup od C jer svaki realni broj x možemo shvatiti
kao kompleksni broj x + 0 f 1. Brojeve kojima je realni dio nula zovemo čisto
imaginarnima.
Napomena 1.
Za one koji znaju defniciju dimenzije vektorskog prostora: Po defniciji C
je dvodimenzionalni vektorski prostor (nad realnim brojevima). Kako mu bazu čine 1 te i,
možemo ga interpretirati kao i svaki drugi realni dvodimenzionalni vektorski prostor:
pomoću koordinatnog sustava u ravnini.
2
Oznaka i za imaginarnu jedinicu potječe iz 18. stoljeća, kad ju je uveo švicarski matematičar L. Euler.
3
Linearne kombinacije su izrazi oblika fx + fy + : : :, gdje su f; f; : : : skalari, a x; y; : : : vektori.
2
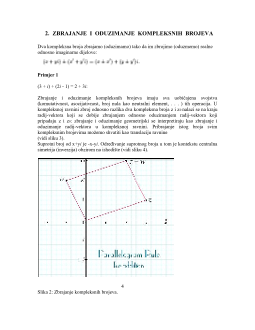
2. ZBRAJANJE I ODUZIMANJE KOMPLEKSNIH BROJEVA
Dva kompleksna broja zbrajamo (oduzimamo) tako da im zbrojimo (oduzmemo) realne
odnosno imaginarne dijelove:
Primjer 1
(3 +
i
) + (2
i
- 1) = 2 + 3
i
:
Zbrajanje i oduzimanje kompleksnih brojeva imaju sva uobičajena svojstva
(komutativnost, asocijativnost, broj nula kao neutralni element, . . . ) tih operacija. U
kompleksnoj ravnini zbroj odnosno razlika dva kompleksna broja z i z
0
nalazi se na kraju
radij-vektora koji se dobije zbrajanjem odnosno oduzimanjem radij-vektora koji
pripadaju z i z
0
: zbrajanje i oduzimanje geometrijski se interpretiraju kao zbrajanje i
oduzimanje radij-vektora u kompleksnoj ravnini. Pribrajanje istog broja svim
kompleksnim brojevima možemo shvatiti kao translaciju ravnine
(vidi sliku 3).
Suprotni broj od x+y
i
je -x-y
i
. Određivanje suprotnog broja u tom je kontekstu centralna
simetrija (inverzija) obzirom na ishodište (vidi sliku 4).
4
Slika 2: Zbrajanje kompleksnih brojeva.
