0
SADRŽAJ
UVOD
2
1. CLOS-OVE KOMUTATORSKE MREŽE
3
1.1. Dvostepena Clos-ova mreža 3
1.2. Trostepena Clos-ova mreža 4
1.2.1. Blokiranje u trostepenoj mreži 6
1.2.2. proračun prospojnih tačaka kod Clos-ove strukture
8
1.3. Petostepena Clos-ova mreža 11
2.
PRIMJER KORIŠTENJA CLOSSOVE KOMUTATORSKE MREŽE
13
3. PRIMJER URAĐENOG ZADATKA
14
4. ZAKLJUČAK
15
LITERATURA 16
POPIS SLIKA 17
UVOD
1
Tema ovog seminarskog rada je „Struktura i rad Clos-ove komutatorske mreže“. U
radu najprije sam definisala Clos-ove komutatorske mreže. A zatim sam navela i objasnila
neke od tipova Clos-ovih komutatorskih mreža, kao što su
Dvostepena Clos-ova
Trostepena Clos-ova
Petostepena Clos-ova
Osim toga u ovom seminarskom radu je navedeno gdje se to koristila navedena mreža, kao i
primjer urađenog zadatka koristeći parametre i formule Clos-ove komutatorske mreže.
Clos-ova komutatorska mreža jeste simetrična arhitektura (broj ulaza jednak broju izlaza) kod
koje je broj komutatora unutarnjeg stupnja jednak broju izlaza /ulaza komutacijskog elementa
ulaznog/izlaznog stupnja.
Jedan od primjera gdje se koristi Clossova komutatorska mreža jesu prve analogne telefonske
centrale. 1890. godine realizovana je prva mreža – međusobno povezivanje dva (induktorska)
telefona ostvarivalo se ručnom komutacijom (prevezivanjem) od strane operatora u centrali po
principu Clos-ovog povezivanja.
1.
CLOS-OVE KOMUTATORSKE MREŽE
3
3-o stepeni komutator se relizuje kao Clos mreža . Clos mreža sastavljena od
neblokirajućih komutacionih modula će imati
k
putanja između svakog para ulaz-izlaz i biće
striktno neblokirajuća ako je
k
>
2
n
−
1
gde je
n
broj po pojedinačnom komutatoru u prvom
stepenu, a
k
je broj individualnih komutatora u drugom stepenu. Posmatrajmo jedan trostepeni
komutator sa prostornom komutacijom. N ulaznih linija se distribuira preko
m
=
N
/
n
grupa od
n
linija.
2
Pretpostavlja se da je
m
, za svrhe prezentacije, cijeli broj, bez gubitka opštosti. Ima
m
komutacionih elemenata na prvom i trećem stepenu i svaka grupa linija se povezuje na jedan
komutacioni element u prvom stepenu. Slično tome, svaki komutacioni element u trećem
stepenu ima
n
izlaznih linkova.
Postoji
k
komutacionih elemenata na drugom stepenu, pri čemu
k
treba da se odredi. Svaki
komutacioni element na prvom stepenu se povezuje na svih
k
komutacionih elemenata na
drugom stepenu. Slično tome, svaki komutacioni element sa drugog stepena se povezuje na
svakim komutacioni element na trećem stepenu. Dakle, komutacioni na prvom, drugom i
trećem stepenu su
nxk
,
(
N
/
n
)
x
(
N
/
n
)
i
kxn
krosbar komutatori, respektivno. Ova arhitektura
je prikazana na slici 2.
Slika 2. Neblokirajući tro-stepeni komutator dimenzija NxN
2
http://telekomunikacije.etf.bg.ac.rs/predmeti/te5itm/ATMkomplet.pdf
4
Trostepena Clos-ova komutaciona mreža je prikazana na slici 2. Komutatorski moduli su
raspoređeni u tri stepena, i svaki modul je povezan jedinstvenom međuvezom sa svakim
modulom u susjednim stepenima. Moduli su neblokirajući.
Tabela 1. Unkrsne tačke u trostepenom interno neblokirajućem komutatoru
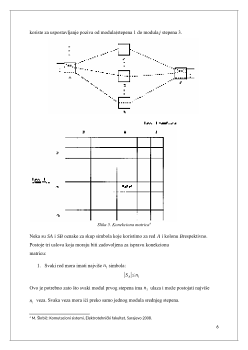
Postoji nekoliko nezavisnih parametara u Clos-ovim mrežama. Postoji r1, r2 i r3modula u
stepenu 1, 2 i 3, respektivno. Dimenzije modula u stepenima 1, 2 i 3 su n1×r2, r1×r3, i r2×r3,
respektivno.
Slika 3. Trostepena Clos-ova mreža za
NxN
komutator
3
3
M. Škrbić: Komutacioni sistemi, Elektrotehnički fakultet, Sarajevo 2008.
