DRŽAVNI UNIVERZITET U NOVOM PAZARU
DEPARTMAN ZA TEHNIČKE NAUKE
SEMINARSKI RAD
KOORDINATNI SISTEMI
Mentor Student
Novi Pazar,mart,2012
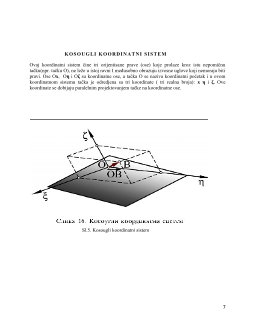
2
S A D R Ž A J
UVOD
………………………………………………………….……….…….3
DEKARTOV KOORDINATNI SISTEM
……………………….….………..4
VIŠEDIMENZIONALNI KOORDINATNI SISTEM
.....................................6
KOSOUGLI KOORDINATNI SISTEM
………………………………...…..7
POLARNO CILINDRIČNI KOORDINATNI SISTEM
..................................8
SFERNI KOORDINATNI SISTEM
.................................................................9
GEOGRAFSKI KOORDINATNI SISTEM
....................................................10
MESNI EKVATORSKI KOORDINATNI SISTEM
......................................11
NEBESKO EKVATORSKI KOORDINATNI SISTEM
..............................12
REFERENTNI KOORDINATNI SISTEM
....................................................13
DRŽAVNI KOORDINATNI SISTEM
……………………………….……..14
LITERATURA
……………………………………………………….……...15
4
D E K A R T O V K O O R D I N A T N I S I S T E M
Dekartov koordinatni sistem
(DKS) se koristi u matematici za jednoznačno definisanje položaja
tačaka u prostoru. Karakteristika ovog sistema je da su njegove koordinatne
ose međusobno normalne.
Dekartov koordinatni sistem je izmislio francuski matematičar i filozof Rene Dekart, koji je,
između ostalih stvari, pokušavao da spoji algebru i Euklidsku geometriju. Ovaj rad je mnogo
uticao na razvoj analitičke geometrije, računa i kartografije.
Ideja o ovom sistemu je razvijena 1637. u dva Dekartova dela. U drugom delu svog Metoda
predavanja, Dekart je uveo novu ideju određivanja položaja tačke ili predmeta na površini,
koristeći dve normalne ose kao pomagalo za merenje. U Geometriji, Dekart je dalje objasnio gore
spomenuti koncept.
Dvodimenzioni Dekartov koordinatni sistem
se koristi da jednoznačno odredi svaku tačku u
ravni pomoću dva broja, koji se obično označavaju sa
x
i
y
. Dekartov koordinatni sistem je
definisan sa dve ose (
x
-osa ili
apcisa
i
y
-osa ili
ordinata
). Izborom mere za svaku osu i
označavanjem jedinica mere duž osa formira se skala.
Korišćenjem Dekartovog koordinatnog sistema geometrijske figure (kao što su krive) se mogu
iskazati algebarskim jednačinama, tj. jednačinama koje zadovoljavaju koordinate na tačkama
koje leže na figuri. Na primer, krug poluprečnika 2 se može prikazati formulom
x
2
+
y
2
= 4.
Sl.1.2. Dvodimenzioni Dekartov koordinatni sistem
5
Trodimenzionalni koordinatni sistem
određuje položaj tačke u prostoru gde je takav
koordinatni sistem definisan središtem koordinatnog sistema
0
, i tri orijentisane ose (
x
,
y
i
z
) s
odgovarajućim jediničnim dužinama. Koordinate svake tačke u takvom sistemu zadate su
uređenim skupom od 3 broja koji označavaju odgovarajuće koordinate u trodimenzionalnom
matematičkom prostoru, gde su koordinate predstavljene orijentisanim udaljenostima od neke
tačke do odgovarajuće ravni. U trodimenzionalnom koordinatnom sistemu nazivi osa (apscisa i
ordinata) nisu uslovne,ali ako se koriste tada je uobičajeno treću,
z
-osu, nazvati aplikata. Na isti
način je uobičajeno
x
-osu i
y
-osu postaviti u horizontalnu ravninu, a preostalu,
z
-osu postaviti
normalno na njih. Trodimenzionalni koordinatni sistem dijelimo na osam područja, “oktanata”,
ograničenih odgovarajućim delovima ravni. Prvi oktant je onaj gde su sve tri poluose pozitivne.
Sl.3.
Trodimenzionalni koordinatni sistem
Sl.4. Levi i desni pravougli koordinatni sistem
