Univerzitet u Nišu
Elektronski fakultet
Katedra za Mikroelektroniku
Predmet:
Laserska tehnika
- Seminarski rad-
tema:
Laseri – princip rada i vrste lasera
Studenti:
Cvetanović Predrag 14242
2012/2013
Laseri – princip rada i vrste lasera
2013
2. Osnovni principi
2.1 Spontana i stimulisana emisija. Apsorpcija
Procesi spontane i stimulisane emisije i apsorpcije, do kojih dolazi pri interakciji elektromagnetnih
talasa sa materijom, su tri fundamentalne pojave koje se koriste u laserima (slika 1.1).
Slika 1.1
–
Šematski dijagram procesa spontane emisije (a), stimulisane emisije (b) i apsorpcije (c).
- Spontana emisija
Pod pojmom sredine podrazumijevat ćemo sistem atoma ili molekula koji se karakteriše skupom
kvantnih stanja i njima odgovarajućih energija. Izdvojimo iz toga skupa dva energetska nivoa:
osnovni nivo 1 sa energijom
E
1
i pobuđeni nivo 2 čija je energija E
2
(
E
2
>E
1
, slika 1.1a). Neka se
u početnom trenutku sistem nalazi u stanju koje odgovara nivou 2. Pošto je
E
2
>E
1
, atom teži da
pređe na nivo 1. Pri tome prelazu izdvaja se energija
E
2
– E
1
, i to: a) kao energija spontano
emitovanog fotona
h
ν, b) bez emisije fotona (npr., energija prelazi u kinetičku energiju okolnih
molekula). Nas će interesovati samo prva mogućnost prelaza.
h
je Planckova [Max Planck (Maks
Plank), 1858.-1947., Nobelova nagrada 1918.] konstanta,
h
= −6.626 10
-34
, J s (za tačne vrednosti
fundamentalnih fizičkih konstanti videti dodatak), a ν frekvencija emitovanog zračenja:
v
= (
E
2
- E
1
)
/
h
. (1.1)
Verovatnoća spontane emisije može se definisati na sledeći način. Pretpostavimo da se u
trenutku
t
na nivou 2 nalazi
N
2
atoma (u jedinici zapremine).
N
2
je naseljenost ili populacija
nivoa 2. Brzina prelaza tih atoma na niži nivo, usled spontane emisije, određena je formulom:
( dN
2
/ dt )
sp
= -AN
2
(1.2)
Tu je
A
tzv. Einsteinov [Albert Einstein (Ajnštajn), 1879.-1955., Nobelova nagrada 1921.]
koeficijent koji predstavlja verovatnoću spontane emisije. Veličina
τ
sp
=1/A
je spontano vreme
života.
- Stimulisana emisija
Pretpostavimo ponovo da se u početnom trenutku atom nalazi na višem nivou 2 i da na sredinu
pada elektromagnetni talas frekvencije ν, definisane sa (1.1). Frekvencija upadnog talasa jednaka
Predrag Cvetanovic 14242
Page
4
Laseri – princip rada i vrste lasera
2013
je frekvenciji spontano emitovanog talasa, što znači da postoji mogućnost da upadni talas
stimuliše prelaz atoma sa nivoa 2 na nivo 1. Pri tome će se razlika energija
E
2
–
E
1
izdvojiti u
vidu elektromagnetnog talasa koji će biti dodan upadnom (slika 1.1b). Između procesa spontane i
stimulisane emisije postoji bitna razlika. U slučaju spontane emisije atom emituje
elektromagnetni talas čija faza i smer prostiranja mogu biti različiti od talasa emitovanog drugim
atomom te iste sredine. Za razliku od toga, u slučaju stimulisane emisije, pošto je proces iniciran
upadnim
elektromagnetnim talasom, emisija svih atoma te sredine se dodaje tom upadnom talasu i
ima istu fazu i smer prostiranja. Proces stimulisane emisije može se opisati formulom:
( dN
2
/ dt )
st
= -W
21
N
2
,
(1.3)
gde je
( dN
2
/ dt )
st
brzina prelaza na račun stimulisane emisije. Verovatnoća stimulisane emisije
W
21
,
za razliku od verovatnoće spontane emisije
A
, zavisi ne samo od konkretnog prelaza, već i od
intenziteta upadnog elektromagnetnog talasa, tačnije:
W
21
=
σ
F
, (1.4)
gde je
F
gustoća fluksa fotona u upadnom talasu, a
σ
21
presek za stimulisanu emisiju, koji zavisi
samo od karaktera datog prelaza. Ako dimenziju dužine označimo sa L, a dimenziju vremena sa
T, tada veličina
σ
21
ima dimenziju površine ,
F
dimenzija 1/(L
2
T) (broj fotona koji u jedinici
vremena prođu kroz jedinicu površine), a
W
21
dimenziju 1/ T .
- Apsorpcija
Pretpostavimo sada da se atom nalazi na nivou 1 i da na sredinu pada elektromagnetni talas
frekvencije ν, (1.1). Verovatnoća prelaza sa nivoa 1 na nivo 2 (slika 1.1c), tj. verovatnoća
apsorpcije , se definiše formulom:
dN
1
/ dt = - W
12
N
1
, (1.5)
gde je
N
1
naseljenost nivoa 1. I ovde, baš kao i za formulu (1.4), vredi:
W
12
=σ
12
F, (1.6)
gde je σ
12
presek za apsorpciju. Einstein je pokazao da je σ
12
= σ
12
= σ, gde je sa σ označen
presek datog prelaza 1
↔
2.
Tri procesa koja smo upravo opisali i koji su predstavljeni na slici 1.1, na “jeziku fotona” mogu
se opisati na sledeći način: a) pri spontanoj emisiji atom, emitujući foton, prelazi sa nivoa 2 na
nivo 1, b) pri prinudnoj emisiji upadni foton izaziva prelaz 2
→
1, usled čega dobijamo dva
fotona (upadni plus emitovani), c) pri apsorpciji upadni foton se apsorbuje, izazivajući prelaz 1
→
2.
Predrag Cvetanovic 14242
Page
5
Laseri – princip rada i vrste lasera
2013
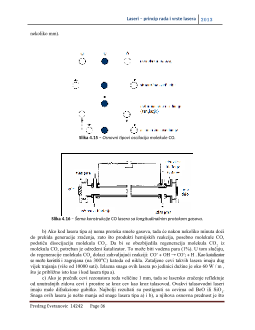
Ravni elektromagnetni talas koji se prostire u smeru normalno na ogledala će se naizmenično
reflektovati od njih, pojačavajući se pri svakom prolazu kroz aktivnu sredinu. Ako je jedno od
ogledala delimično propusno, tada se na izlazu iz sistema može izdvojiti snop korisnog zračenja.
I kod masera i kod lasera generacija je moguća ako je zadovoljen neki granični uslov – prag
generacije. Npr., kod lasera do generacije dolazi u slučaju kada pojačanje aktivne sredine
kompenzuje gubitke u njoj (u gubitke ubrajamo i “korisne gubitke” na račun izlaza zračenja kroz
delimično propusno ogledalo). Na osnovu jednačine (1.7), pojačanje zračenja za jedan prolaz u
aktivnoj sredini (tj. odnos izlazne i ulazne gustoće fluksa fotona) je
exp[ σ(N
2
– N
1
)l]
gde je
l
dužina aktivne sredine. Ako sa
R
1
i
R
2
označimo koeficijente refleksije ogledala, tada su gubici
R
1
R
2
i prag generacije se dostiže ako je:
R
1
R
2
e
2σ(N2 – N1)l
=
1 (1.9)
tj. kada inverzija naseljenosti
N
2
– N
1
dostigne tzv. kritičnu inverziju:
(1.10)
Tek kada je dostignuta kritična inverzija moguće je razlikovati generaciju od spontane emisije
zračenja. Upravo opisani mehanizam čini osnovu laserskih generatora – lasera.
2.3 Stvaranje inverzne naseljenosti
Razmotrimo sada kako se može postići inverzija naseljenosti. Na prvi pogled izgleda da se to
može postići u sistemu sa dva nivoa i sa dovoljno jakim elektromagnetnim poljem frekvencije ν,
(1.1). Pošto je u termodinamičkoj ravnoteži nivo 1 naseljeniji od nivoa 2, apsorpcija će
prevladati prinudnu emisiju, tj. biće više prelaza 1
→
2 nego prelaza 2
→
1. Problem nastupa
kada postane
N
1
= N
2
. Tada se procesi prinudnog zračenja i apsorpcije uzajamno kompenziraju i,
u skladu sa (1.7), sredina postaje propusna za elektromagnetne talase frekvencije ν. Tada se
obično govori o zasićenju sistema sa dva nivoa.
Dakle, koristeći samo dva nivoa nije moguće ostvariti inverziju naseljenosti (videti detaljnije
objašnjenje u trećem poglavlju). Postavlja se pitanje da li se to može postići sa tri ili više nivoa.
Pokazuje se da može, i, u zavisnosti od broja “radnih” nivoa iz (neograničenog) skupa stanja
atomskog sistema, govorićemo o sistemu sa 3, 4 i više nivoa. Kod laserskog sistema sa tri nivoa
atomi se prvo prevode sa osnovnog nivoa 1 na nivo 3 (slika 1.4a). Ako je izabrana takva sredina
u kojoj atom, kada se nađe na nivou 3, brzo prelazi na nivo 2, tada se u takvoj sredini može
ostvariti inverzija naseljenosti između nivoa 2 i 1.
Kod laserskog sistema sa četiri nivoa atomi se takođe prevode sa osnovnog nivoa (označimo ga
sada kao nulti nivo) na nivo 3. Ako nakon toga atomi brzo prelaze na nivo 2, tada će se između
nivoa 2 i 1 pojaviti inverzija naseljenosti. Kada kod takvog lasera sa četiri nivoa dođe do
generacije, atomi pri procesu prinudne emisije prelaze sa nivoa 2 na nivo 1. Zato je, za
neprekidan rad lasera sa četiri nivoa, neophodno da atomi koji se nađu na nivou 1 vrlo brzo
prelaze na nulti nivo. Inverziju naseljenosti je lakše postići kod lasera sa četiri nivoa. Pošto je
obično E
2
– E
1
>> k
B
T, u skladu sa Boltzmannovom statistikom [videti formulu (1.8)] gotovo svi
atomi se pri termodinamičkoj ravnoteži nalaze u osnovnom stanju. Zato je kod sistema sa tri
nivoa potrebno prevesti više od polovine atoma sa osnovnog nivoa 1 preko nivoa 3 na nivo 2, da
Predrag Cvetanovic 14242
Page
7
