1
J.U.UNIVERZITET U TUZLI
FILOZOFSKI FAKULTET
ODSJEK:TEHNIČKI ODGOJ I INFORMATIKA
AKADEMSKA:2013/2014
PREDMET:AUTOMATIKA
SEMINARSKI RAD
TEMA:
MATEMATIČKO MODELIRANJE TERMIČKIH SISTEMA
Temu pripremili: Profesor
Adnan Kuduzović prof.dr.sci.Zenan Šehić,van. Prof
Emir Bašić
2
Matematički modeli sistema
U analizi i sintezi SAU se koriste kvantitativni matematički modeli koji opisuju fiziku sistema.
Generalno, dinamika sistema je opisana običnim diferencijalnim jednačinama. Klasa sistema koja
će se proučavati u toku ovog kursa su: kontinualni, linearni, stacionarni sistemi sa koncentrisanim
parametrima. Takvi sistemi se opisuju sistemima linearnih diferencijalnih jednačina sa konstantnim
koefeicijentima.
Obzirom da je veliki broj fizičkih sistema nelinearan, u okviru ove teme će se govoriti i o
linearizaciji, koja omogućava primenu Laplasove transformacije (Laplace). Takođe, biće reči i o
Laplasovoj transformaciji kao veoma korisnom alatu za rešavanje problema opisanih
diferencijalnim jednačinama. Obradiće se relacije ulaz-izlaz (RUI) i funkcija prenosa sistema, a
u okviru grafičkih metoda predstavljanja sistema blok dijagram, graf toka signala i njihove
transformacije (simplifikacija, uprošćavanje).
Uvod
Da bi se razumjela dinamika i projektovalo upravljanje za neki kompleksan sistem prvo mora biti
poznat njegov matem
a t i čki
mode
l . Pošto su razmatrani sistemi u prirodi dinamički, za njihovo
opisivanje se koriste sistemi diferencijalnih jedn
a čina
(DJ
) . Pri rešavanju sistema diferencijalnih
jednačina pogodno je koristiti Laplasovu
transformaciju
(LT) koja pojednostavljuje određivanje
rešenja. Ukoliko je SAU opisan sistemom nelinearnih DJ pre primene LT je potrebno izvršiti
linearizacij
u . U praksi, sistemi koji se
razmatraju mogu biti veoma komplikovani, ili njihova priroda nije u potpunosti poznata te je u
procesu modelovanja potrebno uvesti (usvojiti) određene pretpostavke, zanemarenja i uprošćenja.
Nakon završenog modelovanja SAU je opisan sistemom linearnih DJ. Na kraju se na osnovu
postavljenog modela, primenom LT, određuje ponašanja sistema u različitim uslovima i za
različite pobude.
Analiza dinamičkih sistema se prema dosad navednom može raščlaniti na sledeće korake:
1. Definisanje sistema i njegovih komponenti;
2. Formulisanje matematičkog modela uz nabrajanje usvojenih pretpostavki;
3. Pisanje sistema DJ koji opisuje model (sistem);
4. Rešavanje postavljenog sistema jednačina po željenim izlaznim promenljivima;
5. Provera tačnosti rešenja i usvojenih pretpostavki;
6. Ako je potrebno, ponovo proanalizirati sistem i ponovo formulisati model.
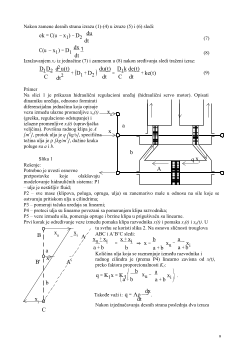
Primer: Van der Pol–ov oscilator
Električno kolo sa slike 1 proizvodi oscilacije u prisustvu nelinearnog elementa – triode. U triodi
elektroni se emituju sa grejača (katode) i prelaskom na anodu (pozitivnog potencijala
e
p
) formiraju
struju kroz triodu (
i
p
). Negativan potencijal mrežice (eg) se upotrebljava za upravljanje tom
strujom. Struja kroz mrežicu se zanemaruje.
4
⎞
di di di
Sada se uvodi smena:
e=e
p
+µe
g
=E
bb
-L
dt
+µM
dt
=E
bb
+(µM-L)
dt
. (9)
y=i-φ(E
bb
) (10)
Nakon uvođenja smene (10) izraz (6) se može napisati u obliku:
2
⎛
dy
⎞
LC
d y
L
⋅
dy
+y+φ(E )=φ
⎜
E +(µM-L)
⎜
. (11)
Ako je:
dt
2
+
R dt
bb
⎝
bb
dt
⎠
⎛
dy
⎞
⎛
dy
⎞
⎜
⎜
=φ
⎜
E
bb
+(µM-
L)
⎜
-φ(E
bb
), (12)
f
⎝
dt
⎠
⎝
dt
⎠
izraz (11) se može napisati u obliku:
2
⎛
dy
⎞
LC
d y
L
⋅
dy
⎜
⎜
. (13)
dt
2
+
R dt
+y=f
⎝
dt
⎠
Razvojem (12) u Tejlorov red dobija se izraz:
3
⎛
dy
⎞
dy 1
⎛
dy
⎞
2
1
⎛
dy
⎞
⎜
⎜
=φ(E
bb
)−φ(E
bb
)+φ'(E
bb
)(µM-L)
+ φ''(E
bb
)
⎜
(µM-L)
⎜
+ φ'''(E
bb
)
⎜
(µM-L)
⎜
+...
f
⎝
dt
⎠
Pošto je P prevojna tačka važi:
dt 2
⎝
dt
⎠
6
⎝
dt
⎠
(14)
φ''(E
bb
)=0. (15a)
Dodatnom analizom slike 2 može se zaključiti:
φ'(E
bb
)>0, φ'''(E
bb
)<0, (15b)
a takođe važi i uslov:
µM-L>0 za µ>>1 (15c)
Uz uvažavanje izraza (15) i uz zanemarivanej članova višeg reda, izraz (14) se može napisati
u obliku:
⎛
dy
⎞
dy 1
⎛
dy
3
⎜
⎜
=φ'(E
bb
)(µM-L) + φ'''(E
bb
)
⎜
(µM-L)
⎜
(16)
f
⎝
dt
⎠
Nakon zamene (16) u (13) sledi:
2
dt 6
⎝
dt
⎠
⎛
dy
⎞
3
LC
d y
L
⋅
dy
+y=φ'(E )(µM-L)
dy
+
1
φ'''(E
)
⎜
(µM-L)
⎜
. (17)
dt
2
+
R dt
bb
dt 6
bb
⎝
dt
⎠
Ako se definišu veličine α i β na sledeći način:
L
R
-φ'(E
bb
)(µM-L)=-α, α>0 za µ>>1; (18)
1
3
β
5
⎣
6
φ'''(E
bb
)(µM-L) =-
3
, β>0; (19)
izraz (17) se može napisati u obliku:
2
⎛
dy
⎞
3
LC
d y
dy
+
β
⎜ ⎜
+y=0. (20)
dt
2
-α
dt
3
⎝
dt
⎠
Uvode se sledeće oznake: ω
2
=
1
; τ=ωt; y=
α
⋅
z
; ε=αω pa se izraz (20) može napisati u
obliku:
d
2
z
LC β ω
⎡
dz 1
⎛
dz
⎞
3
⎤
⎜
⎜
⎜
⎜
+z=0 (21)
dτ
2
-ε
dτ
-
3
⎝
dτ
⎠
⎦
Ako se izvrši diferenciranje izraza (21) po τ i uvede smena:
dz
=x, dobija se Van der Polova dτ
jednačina:
d
2
x
2
dx
dτ
2
+ε(x -1)
dτ
+x=0 (22)
7
G = 1/R L C
i
g
i
l
i
c
dt
,
2
L
i(t)
u(t)
Slika 2.
Električno kolo sa slike 2 se može opisati sledećim izrazom
1
t
0
du(t)
i(t) = ig + il + ic = Gu(t) + L
0
u(t)dt +
Ê
I
L0
+ C
dt
Pošto je: u(t) =
dΨ (t)
prethodni izraz se može napisati
d 2 Ψ
(t)
i(t) = C
dt
dΨ (t)
+ G dt +
i
Ψ(t). (2)
Ako se posmatraju jednačine (1) i (2) vidi se da su one istog oblika, iako opisuju fizički
različite pojave (sisteme). Na osnovu
istog oblika je
d
načina
uspostavljaju se sledeće
analogije:
Mehaničke veličine
Električne veličine
sila f(t)
↔
struja i(t)
položaj y(t)
↔
fluks Ψ(t)
masa M
↔
kapacitivnost C
trenje b
↔
provodnost G
krutost (elastičnost) K
↔
recipročna vrednost induktivnosti 1/L
Jednačine (1) i (2) se mogu rešiti nekom od metoda za rešavanje DJ (metoda neodređenih
koeficijenata).
Neka je za DJ (1) y(t
0
)=Y(0)=0 i f(t)=F=const., tada je rešenje
-α
1
t
y(t) = K1e
sin(β1t + θ1), (3)
gde su K
1
, α
1
, β
1
i θ
1
koeficijenti koje treba odrediti.
Za rešenje jednačine (2), uz uslove: u(t
0
)=0 i i(t)=I=const., se dobija:
-α2t
u(t) = K2e
sin(β2t + θ2) (4)
