FI
ZIČKO
-
TEHNIČKA MERENJA
2012,
Marko Barjaktarović
UVOD
•
Rezultat svakog merenja sadrži određenu nesigurnost.
•
Tačnu vrednost merne veličine nije moguće odrediti.
FI
ZIČKO
-
TEHNIČKA MERENJA
2012,
Marko Barjaktarović
UVOD
•
U cilju uvođenja standardizacije u oblast izražavanja mernih rezultata,
uveden je pojam merne nesigurnosti – Uncertainty in Measurement.
• Osnova uputstva za izražavanje merne nesigurnosti – ISO Guide to the
Expression of Uncertainty in Measurement
, skraćeno GUM.
• Postoji nekoliko revizija GUM-a, prva verzija izdata 1993. godine.
• Trenutna verzija:
http://www.bipm.org/en/publications/guides/
• Merna nesigurnost je parametar koji se pridružuje rezultatu merenja i koji
odražava rasipanje izmerenih vrednosti.
•
Svi faktori koji utiču na rezultat merenja potencijalni su uzročnici merne
nesigurnosti.
•
Identifikacijom tih faktora i procenom njihovih vrednosti moguće je
unaprediti proceduru merenja, a time i smanjiti mernu nesigurnost.
• Cilj –
ne samo smanjenje vrednosti merne nesigurnosti, već otkrivanje svih
faktora koji mogu uticati na mernu nesigurnost.
FI
ZIČKO
-
TEHNIČKA MERENJA
2012,
Marko Barjaktarović
STATISTIČKA OBRADA MERNIH REZULTATA
•
Ponovljenim merenjem posmatrane fizičke veličine dobijen skup rezultata (uzorak):
1
2
3
1
...
1
n
n
s
i
i
x
x
x
x
x
x
n
n
1
2
3
, , ,...,
n
x
x
x
x
• Srednja vrednost uzorka:
• Standardno odstupanje uzorka:
2
1
1
n
i
s
i
x
x
s
n
• Standardno odstupanje srednje vrednosti (dobija se od n merenja i tih n
merenje je takođe
slučajno određeno):
2
1
1
s
n
i
s
x
i
x
x
s
n n
•
Srednja vrednost je pouzdanija od pojedinačnih merenja.
• Relativno standardno odstupanje (što ima manju vrednost ponovljivost je
bolja):
r
s
s
s
x
FI
ZIČKO
-
TEHNIČKA MERENJA
2012,
Marko Barjaktarović
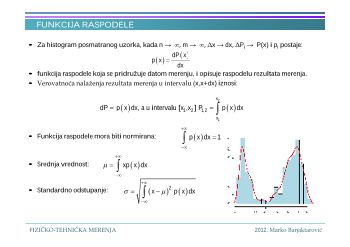
HISTOGRAM
• Histogram –
grafička predstava rezultata merenja.
• Histogram prikazuje grupisanje oko srednje vrednosti –
omogućuje brzu procenu funkciju
raspodele koja opisuju posmtaranu mernu veličinu.
• Posmatra se uzoraka: x
1
, x
2
, x
3
,..., x
n
.
• Svi rezultati merenje nalaze se u intervalu [x
min
, x
max
].
•
Određuje se broj intervala histograma
m
, najčešće je:
•
Širina histograma Δ
x
iznosi:
•
U svakom intervalu nalazi se rezultata merenja (učestanost intervala).
•
Svakom intervalu odgovara relativna učestanost:
i
x
n
max
min
x
x
x
m
2
ili
log
1
m
n
m
n
i
x
i
n
P
n
