Dr. Aca Jovanovi}, dipl.ing.
METODE OPERACIONIH ISTRA@IVANJA
1
UVOD
Predmet kojim se bave operaciona istra`ivanja je upravljanje organizacionim,
tehni~kim i drugim slo`enim sistemima. Cilj je iznala`enje optimalnih rezultata za
pripremanje i dono{enje upravlja~kih odluka i pra}enje njihovog izvr{enja. Osnovna
karakteristika savremenog (postindustrijskog) dru{tva je postojanje slo`enih sistema.
Primeri slo`enih tehni~kih sistema su: tehnolo{ko-proizvodni, energetski,
komunikacioni, transportni sistemi, vodosnabdevanje.
U okviru slo`enih sistema su podsistemi i njihovi elementi sa vezama i interakcijama
izmedju sebe i izmedju sistema i njegove okoline.
Slo`eni sistemi se sastoje od podsistema i elemenata, sa razli~itim nivoima veza
izmedju elemenata ( od veoma slabih do krutih), sa medjusobnim uticajima koji mogu
biti deterministi~ki ili stohasti~ki, sa slede}im glavnim karakteristikama:
vi{ekriterijumski cilj, pri ~emu su lokalni podciljevi ~esto u koliziji,
hijerarhijska struktura sistema, sa jasno definisanim podsistemima do
elementarnog podsistema - elementa sistema,
definisana je granica sistema, sa izra`enim medjusobnim uticajima sistema i
okruzenja,
rast sistema.
U ovakvim uslovima, upravljanje se mora vr{iti metodi~no, sa programom. Pod
programom se podrazumeva planiranje odluka - plan i upravljanje realizacijom plana.
U ovim predavanjima te`i{te je dato razvijenim metodama operacionih istra`ivanja,
mogu}nosti njihove primene a kroz prikaz razli~itih primera i razvijenog softvera.
Operaciona istra`ivanja su nastala po~etkom ~etrdesetih godina u Velikoj Britaniji,
formiranjem grupe istra`iva~a, ~iji je osnovni zadatak bio da "primenom postoje}ih i
razvojem novih nau~nih metoda na kvantitativnim osnovama daju odgovore po pitanju
najboljeg ili "dovoljno dobrog" funkcionisanja: tehni~kih, organizacionih, ekonomskih i
drugih sistema u postoje}im uslovima. Po~etkom pedesetih godina nastavolo se sa
razvojem nove discipline, koja u osnovi sadr`i integraciju raznih disciplina. Za veoma
kratko vreme, ova nauka dala je privredi zna~ajan niz korisnih metoda za re{avanje
Dr. Aca Jovanovi}, dipl.ing.
METODE OPERACIONIH ISTRA@IVANJA
2
brojnih zadataka iz industrije, eksploatacije rudnog bogatstva, transporta, nala`enja
optimalnog proizvodnog programa, utvrdjivanje najboljeg redosleda operacija u
proizvodnji, planiranja realizacije slo`enih projekata i sl.
U okviru predavanja bi}e obradjene slede}e oblasti i teme:
1.
Upotreba modela i prilaz prou~avanju
2.
Linearno programiranje
3. Nelinearno
programiranje
4. Dinami~ko
programiranje
5. Optimalno
rezerviranje
6. Teorija
igara
7.
Mre`no planiranje (tro{kovi i resursi)
8.
Teorija redova ~ekanja
9.
Simulacija proizvodnih procesa
10. Upravljanje
zalihama
1.0. UPOTREBA MODELA I PRILAZ PROU^AVANJU
Osnovna ideja operacionih istra`ivanja je ista kao i u bilo kojoj drugoj nau~noj
disciplini, a to je izgradnja modela. Bitna razlika se sastoji u tome {to se operaciona
istra`ivanja bave sistemima kojima se mo`e rukovati i kojima se mo`e upravljati.
Model je koristan u najmanje sedam slede}ih funkcija: (1) kao pomo} u razmi{ljanju,
(2) kao pomo} u komuniciranju, (3) kao orudje za prognoziranje, (4) kao pomo} u
upravljanju, (5) kao sredstvo za obuku i instrukta`u, (6) za analizu osetljivosti i (7) kao
pomo} pri dono{enju odluke.
Interesantna je sedma funkcija – model kao pomo} pri dono{enju odluka. Poznato je
da postoje tri nivoa odluka:
strate{ki, takti~ki i tehni~ki (operativni).
Od samog
po~etka su operaciona istra`ivanja kori{}ena i primenjivana na razli~ite probleme kao
pomo} u dono{enju odluka. Medjutim, ve}ina ovih odluka je po svojoj prirodi bila
takti~ka. Operaciona istra`ivanja su veoma retko kori{}ena za dono{enje tehni~kih
odluka. Razlika izmedju strate{kih i takti~kih odluka sastoji se najmanje od tri
Dr. Aca Jovanovi}, dipl.ing.
METODE OPERACIONIH ISTRA@IVANJA
4
2.0. LINEARNO PROGRAMIRANJE (LP)
U savremenim uslovima menad`menta u privredi, vanprivrednim delatnostima, vojsci,
ili u dr`avi u celini, pojavljuju se problemi koji po pravilu imaju vi{e alternativnih
re{enja. Uloga menad`era je, da polaze}i od odredjenih zakonitosti, usvojene
strategije, zahteva i ograni~enja odabere ona re{enja koja su u datim uslovima
optimalna.
Zadaci koji se re{avaju su:
-
optimalno planiranje investicionog ulaganja,
-
definisanje optimalnog proizvodnog programa,
-
izbor lokacije kompanije, pojedinih pogona ili postrojenja unutar kompanije, ili
razme{taj ma{ina i radnih mesta u jednom pogonu,
-
izbor i razme{taj sredstava naoru`anja,
-
izbor optimalne varijante tehnolo{kog procesa,
-
sastavljanje optimalnih planova (transporta, ishrane, zaliha), itd.
Kod re{avanja ovih zadataka primenjuje se kriterijum maksimuma ili minimuma. Na
maksimum treba dovesti prihod ili profit, iskori{}enje resursa, produktivnost, gotovost,
raspolo`ivost itd. Na minimum treba svesti utro{eno vreme za realizaciju neke
aktivnosti, tro{kove, utro{ak materijala, vreme i distance transporta robe ili
poluproizvoda itd.
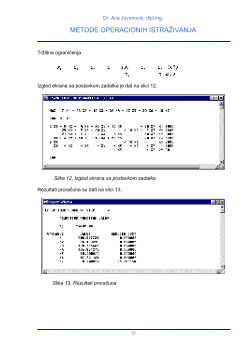
Zadaci koji se sa aspekta matemati~kog modela M svode na linearno programiranje
svode se na fukciju cilja (funkciju kriterijuma) F(X), koja predstavlja linearnu
kombinaciju nepoznatih, pri odredjenom skupu ograni~enja L, koja su takodje zadata
linearnim jedna~inama ili nejedna~inama.
Matemati~ki, problem se sastoji u tome kako na}i maksimum ili minimum jedne
linearne funkcije F(X) pri datom skupu ograni~enja L.
Postojanje ra~unara i razvijenih softvera omogu}uje brzo dobijanje re{enja u
problemima sa velikim brojem promenljivih i u razli~itim varijantama, {to omogu}uje
eksperimentisanje na modelu.
Najve}a pa`nja se posve}uje zapravo jasnoj formulaciji zadatka i pravilnoj postavci
problema. Za prakti~are iz ove oblasti vi{e nije pitanje kako re{avati zadatke LP-a,
nego kako takve probleme u praksi otkrivati i pravilno formulisati. Ovde u punom
Dr. Aca Jovanovi}, dipl.ing.
METODE OPERACIONIH ISTRA@IVANJA
5
zna~enju dolazi do izra`aja poznata izreka u matematici “jasno formulisan problem je
vi{e nego polovina re{enja”.
2.1. Op{ta formulacija zadatka Linearnog Programiranja (LP)
Op{ta matemati~ka formulacija zadatka LP se sastoji u tome da se odredi takav skup
vrednosti
n
x
x
x
,....
,
2
1
, koje su komponente n-dimenzionog vektora
[
]
n
x
x
x
X
.....
,
2
1
=
iz
oblasti D, koja je zadana sistemom linearnih jedna~ina i/ili nejedna~ina,
)
,...
2
,
1
(
,
0
,...,
1
,
1
n
j
x
m
i
b
x
a
j
i
m
j
j
ij
=
≥
=
≥
=
≤
∑
=
(1)
za koje je funkcije cilja (ili kriterijuma):
( )
∑
=
=
n
j
j
j
x
c
X
F
1
(2)
dosti`e ekstremnu vrednost (maksimum ili minimum).
2.2. Grafi~ka metoda
Grafi~ka metoda je veoma prikladna i pregledna, ali se mo`e primenjivati na probleme
linearnog programiranja sa dve nepoznate.
Sistem ograni~enja je:
m
i
b
x
a
x
a
i
i
i
,...,
1
,
2
2
1
1
=
≥
=
≤
+
Ovaj sistem treba predstaviti grafi~ki, u koordinatnom sistemu x
1
-x
2
, a zatim za
postavljenu funkciju cilja, koja u ovom slu~aju ima oblik
( )
2
2
1
1
x
c
x
c
X
F
+
=
odrediti minimalnu, odnosno maksimalnu vrednost. Grafi~ki prikaz ograni~enja je
konkavna (konveksna) oblast dopustivih rešenja
D
, preko koje se translira funkcija
cilja
( )
0
=
X
F
, i odredjuje njen minimum, odnosno maksimum.
Dr. Aca Jovanovi}, dipl.ing.
METODE OPERACIONIH ISTRA@IVANJA
7
Rešenje:
a. Minimalnu vrednost funkcija kriterijuma dosti`e u ta~ki
( )
1
,
5
B
*
, koja je u preseku
pravih
p
1
i
p
2
. Imamo da je:
( )
3
5
1
2
,
1
5
min
*
−
=
−
⋅
=
=
=
=
B
B
X
F
F
X
X
b. Maksimalnu vrednost funkcija kriterijuma dosti`e u ta~ki
( )
3
,
3
A
, koja je u preseku
pravih
p
1
i
p
3
.
( )
3
3
3
2
X
F
F
3
3
X
X
A
A
=
−
⋅
=
=
=
=
max
*
,
Rešavanje zadatka je prikazano na slici 2. Oblast dopustivih rešenja (trougao) je
predstavljena podebljano i ozna~ena sa
D
.
Slika 2. Grafi~ko re{enje Primera 1
