УНИВЕРЗИТЕТ У БЕОГРАДУ
ГРАЂЕВИНСКИ ФАКУЛТЕТ
ОДСЕК ЗА ГЕОДЕЗИЈУ И ГЕОИНФОРМАТИКУ
Ђорђе Грујичић инж. геод.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ
ГРАДА КРАЉЕВА ПРИМЕНОМ МЕТОДЕ КОНАЧНИХ
ЕЛЕМЕНАТА
- Мастер рад -
Београд 2019.
Ментор:
доц. др Јован М. Поповић дипл. инж. геод.
Чланови комисије:
проф. др.
Иван Р. Алексић дипл. инж. геод.
доц. др. Милева С. Самарџић Петровић
Датум одбране:
_______________________________________
vi
-
2. Примена Активне геодетске референтне основе Србије у премеру
непокретности – магистарска теза
/
Ј. Поповић//
.
– Грађевински факултет,
Београд, 2010.
-
3. Геодетски премер - Збирка решених задатака
/ И. Р. Алексић
,
Ј. Гучевић и
Ј. Поповић//
.
- Београд: Универзитет у Београду, Грађевински факултет, 2009.
Београд 10.04.2019.
ПРЕДМЕТНИ НАСТАВНИК
доц. др Јован Поповић, дипл. геод. инж.
vii
РЕЗИМЕ
Мастер рад посвећен је формулисању одговарајућег модела грид трансфоромације
просторних података између глобалног и локалног геодетског референтног система
на подручју града Краљева, при чему се у највећој мери обухватају дисторзије и
деформације у реализацији једног или оба система.
Уобичајени начин трансформације између геоцентричног и негеоцентричног
геодетског референтног система (тродимензионална седмопараметарска
трансформација сличности) може се успешно применити само на ограниченим
подручјима због присуства дисторзија (изобличења) у просторним подацима
премера непокретности израженим у Државном координатном систему.
Развој модела грид трансформације за подручје града Краљева извршен је на
основу скупа од 81 тачке премера непокретности израженим у SRB_ETRS89
референтном систему и Државном координатном систему. У оквиру рада
истражена је могућност поступка подела подручја трансформације на коначне
елементе при моделирању дисторзија просторних података. Иако је густина
расположивог узорка недовољна, на основу добијених резултата може се
закључити да је применом овог поступка могуће добити довољно тачан и поуздан
модел грид трансформације података премера у Државни координатни систем.
Кључне речи:
грид трансформација, метод коначних елемената, Хелмертова
трансформација, геодетски референти систем, геодетски датум, моделовање
дисторзија.
Научна област:
Геодезија
Ужа научна област:
Геодетски премер
ix
ПРЕДГОВОР
Овим радом је развијен модел грид трансформације методом коначних елемената за
територију града Краљева. Основни задатак јесте оценити вредности изобличења
просторних података у тачкама правилног грида, који обухвата подручје.
У уводном (првом) поглављу објашњени су основни појмови, дат је кратак опис
дефиниције Државног координатног система, референтног система и референтног
оквира и дефинисан предмет рада са основним циљем.
У другом поглављу дат је опис конвенционалног терестричког референтног система
кроз три основна вида, међународни терестрички референти систем, светски
геодетски референтни систем и параметри земље ПЗ90.
У трећем поглављу описан је европски терестрички референтни систем, његова
имплементација са међународним терестричким референтним системом и његово
успостављање кроз перманентне GNSS мреже и EUREF перманентне мреже – EPN.
У четвртом поглављу приказана је реализација референтног система ETRS89 у
Републици Србији кроз две мерне кампање
Балкан ''98
и
''EUREF СРБИЈА 2010''.
У петом поглављу детаљно је описан државни координатни систем Републике
Србије од успостављања тригонометријске мреже првог реда па све до
успостављања просторног референтног система Републике Србије.
У шестом поглављу приказани су најчешћи модели датумске трансформације
између геоцентричног и негеоцентричног геодетксог референтног система. Такође
приказан је концепт грид трансформације код моделирања дисторзија.
У седмом поглављу дата је основна идеја моделирања дисторзија (изобличења)
просторних података изражених у геодетском референтном систему реализованом
терестричким техникама. Такође је дат математички метод моеделирања дисторзија
– трансформација поделом подручја на коначне елементе.
У осмом поглављу извршен је развој модела грид трансформације методом
коначних елемената шире подручје града Краљева. Модел трансформације развијен
је на основу скупа од 81 тачке премера непокретности са координатама познатим у
оба геодетска референтна система (SRB_ETRS89 и Државни координатни систем).
Моделирање дисторзија података премера непокретности извршено је методом
коначних елемената и извршено је тестирање модела грида.
Сумарни преглед добијених резултата, основни закључак као и могући правац
даљег истраживања приказан је у поглављу 9.
xv
LCM
Linear Combination Model,
LSC
Least
Squares Collocation,
LIM
Linear Interpolation Method,
LLR
Lunar Laser Ranging,
LSM
Low
order Surface Model,
NAVSTAR
NAvigation System with Timing And Ranging,
NIMA
US National Imagery and Mapping Agency,
PP
Precise Positioning,
RTCM
the Radio Technical Commission for Maritime Services,
RTK
Real Time Kinematic,
SLR
Satellite Laser Ranging,
UHF
Ultra High Frequency
UTM
Universal Traverse Mercator,
VHF
Very High Frequency
VLBI
Very Long Base Interferometry,
VRS
Virtual Reference Station,
WGS84
Word Geodetic System 1984,
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
2
стварним координатним вредностима стварних тачака у простору које су доступне
свима. Референтни оквир не може постојати без референтног система, а референти
систем практично нема вредност без референтног оквира.
До преласка на нов државни референтни систем ETRS89 и UTM пројекцију,
положај тачака се изражава дводимензионалним координатама и постојећим
пројекцијама (Гаус – Кригерова, Стереографска и Золднеровој пројекција).
Постојећи државни референтни систем Републике Србије, који је у уптреби већ
више од седамдесет година, заснива се на негеоцентричном Беселовом елипсоиду и
Гаус – Кригеровој пројекцији меридијанских зона.
Разлог за ове промене је пре свега глобалног карактера. У Европи се већ дужи низ
година примењује ETRS89 референтни координатни систем, који користи GRS80
елипсоид. Чињеница да се Србија налази у фази извођења и планирања многих
нових геодетских премера и израде различитих дигиталних база података, као и
неопходност размењивања просторних и за простор везаних података са другим
Европским државама, сасвим су јасно представљали разлоге за увођење новог
референтног координатног система и сњим повезаног референтног елипсоида
GRS80.
Други разлог лежи у чињеници да су мерења обављена применом сателитске
геодезије показала нехомогеност постојеће државне тригонометријске мреже, која
износи 2 до 3 метра.
Увођење новог државног референтног система, који се од постојећег разликује по
положају и по орјентацији и по размери, подразумева формулисање одговарајућег
трансформационог модела којим се остварује веза између постојећег и новог
државног рефернтног система у оба правца, и обухватају у највећој мери дисторзије
и деформације у реализацији једног или оба система.
Успостављање методологије прелаза из старог геодетског датума, који се у пракси
још увек користи и који ће још неко време бити у широј употреби, у јединствен
нови Законом прописани геодетски датум, јесте један од главних циљева данашњих
истраживања. Из практичних разлога тренутно је много интересантнији обрнути
прелаз из савременог опажачког у архивски оквир, односно стари геодетски датум.
Оваква ситуација је директна последица потребе одржавања постојећих података
катастра непокретности, затим још увек до краја неуређене нормативно – правне
регулативе у инжењерско - техничким и другим областима које представљају
најважније кориснике геодетских података и услуга.
Проблем трансформације просторних података из глобалног геодетског
референтног система у локални (или обрнуто) постаје много сложенији ако постоји
присуство дисторзија (изобличења) просторних података изражених у локалном
геодетском референтном систему. Разлог за појаву ових дисторзија, у првом реду,
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
3
је слаба условљеност геодетског референтног оквира реализованог терестричким
техникама (
Jäger и др.
2003). Као резултат јавља се велика зависност релативне
тачности просторног положаја тачака изражених у локалном геодетском
референтном систему од растојања између тачака. У овом случају неопходно је
истражити могућности да се неке (или све) ове дисторзије значајно умање (или
потпуно отклоне) кроз процес трансформације. При томе је неопходно задовољити
све критеријуме које модел трансформације мора да испуни (једноставност,
ефикасност, јединственост и тачност).
Национални модел трансформације података премера непокретности између
геоцентричног геодетског референтног система и националног негеоцентричног
геодетског референтног система реализованог терестричким техникама
позиционирања треба да задовољи следеће критеријуме (
Collier
и др.
1998):
-
Једноставност
, да би се омогућило широко разумевање и примена од стране
корисника,
-
Ефикасност
, да би се минимизирало време и ресурси потребни за рачунање,
-
Јединственост
, да би позицији сваке тачке у једном систему кореспондирала
само једна вредност координата у другом систему и
-
Тачност
, да би се добили најбољи могући резултати трансформације на основу
расположивог узорка просторних података.
Уобичајени поступци датумске трансформације, као што је н.пр.
седмопараметарска трансформација сличности, не даје задовољавајућу тачност за
већа подручја због неизбежних присуства дисторзија (изобличења) у геодетском
референтном оквиру реализованом терестричким техникама (
Collier и др.
1998,
Jäger и др.
2003) узрокованих у првом реду слабом условљеношћу геодетских
мрежа реализованих терестричким техникама. Међутим, ове дисторзије могу се,
применом одговарајућих поступака, на одговарајући начин моделирати и
отклонити. Поступци за моделирање и отклањање дисторзија просторних података
укључују:
- вишеструку регресију (
Applebaum
1982),
- моделирање површи минималне закривљености (
Briggs
1974,
Dewhurst
1990),
- колокацију по методи најмањих квадрата (
Mikhail
1976,
Moritz
1980,
Михаиловић
1984,
Марковић
1990,
Collier
2002) и
- моделирање дисторзија просторних података поделом подручја трансформације
на коначне елементе (
Jäger и др.
2003).
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
5
2.
..
КОНВЕНЦИОНАЛНИ ТЕРЕСТРИЧКИ РЕФЕРЕНТНИ
СИСТЕМИ
Терестрички референтни систем je фиксиран за Земљу као небеско тело и ротира
заједно са њом. Овај координатни систем служи за дефинисање координата тачака
на физичкој површи Земље.
Логично је да координатни почетак буде фиксиран у центру масе Земље а да се оса
Z
подудара са Земљином осом ротације. Оса
X
се може изабрати тако да пролази
кроз тачку пресека екватора и почетног Гриничног меридијана, чиме се обезбеђује
да систем ротира заједно са Земљом.
Y
– оса се бира тако да комплетира систем
десне орјентације.
Овако дефинисан терестрички систем би био сасвим довољан да не постоји један
крупан недостатак. Тај феномен се назива
кретање Земљиног пола
. Тачније оса
Земљине ротације не заузима фиксни положај у телу масе Земље, пол Земљине
ротације се помера током времена у односу на околну Земљину кору по приближно
спиралној путањи чији полупречник не прелази 15 m. Механизам кретања пола није
тачно познат, али се верује да је резултат неке врсте прерасподеле маса унутар
Земљиног тела.
Како је оса Земљине ротације променљива то су и меридијани који су везани за њу
променљиви. Оса Земљине ротације се може одредити астрономским опажањима
или сателитским мерењима, на тај начин се може доћи до средње вредности осе
Земљине ротације. Самим тим се и положај тренутног пола мора директно
одређивати. Проблем је у сваком случају превазиђен на тај начин што је
међународним договором дефинисан средњи положај пола за период од 1900. до
1905. године, под називом
конвенционални терестрички пол (CTP)
- (Слика
2.1.).
CTP дакле одређује орјентацију координатних оса терестричког референтног
система на које се своде опажања и положаји.
Слика 2.1.
Кретање пола за период од 1900. до 1993. године у односу наконвенционални
терестрички пол (CTP).
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
6
Са тако усвојеним средњим положајем пола ротације, сада се може дефинисати
Конвенционални терестричи референтни систем (CTRS)
, на следећи
начин(Слика 2.2.):
- Координатни почетака смештен је у центру масе Земље (укључујући и масу
океана и атмосфере),
- Оса Z
T
поклапа се са средњом осом ротације Земље за период од 1900. до 1905.
Године, односно пролази кроз CTP,
- Оса X
T
пролази кроз тачку пресека СТР екватора и СТР почетног Гриичког
меридијана,
- Оса Y
T
налази се у екваторској равни и комплетира правоугли координатни
систем десне орјентације.
Слика 2.2.
Конвенционални терестрички референтни систем
У конвенционалном терестричком референтном систему координате тачака могу
бити изражене у облику 3-D правоуглих координата (
X,Y,Z
) – Картезијанске
координате и у облику елипсоидних координата (
φ,λ,h
)–Геодетске координате.
Правоугле 3-D координате (
X,Y,Z
) се обично називају геоцентричне координате
фиксиране за Земљу (Earth-Centred-Earth-Fixed – ECEF).
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
8
- Very Long Base Interferometry(VLBI),
- Lunar Laser Ranging (LLR),
- Global Navigation Satellite Systems (у овом тренутку GPS и ГЛОНАСС системи),
- Satellite Laser Ranging(SLR) и
- Doppler Orbitography and Radiopositioning Integratet by Satellite(DORIS).
С обзиром на то да су станице смештене на литосферним плочама које се
међусобно крећу, примена последњег критеријума у горњој ITRS дефиницији
обезбеђује стабилност оријентације координатних оса у односу на Земљину кору.
Геодинамички процеси су истовремено и разлог што IERS периодично реализује
ITRF. Резултати се публикују подознаком ITRFxx, где xx представља последњу
годину чији су подаци опажања коришћени.
Кретање литосферних плоча описује се кроз брзине терестричких тачака
V
(
t
)
уколико су познате координате тачке у епохи
t
0
.
X
(
t
0
)
={
X
(
t
0
)
,Y
(
t
0
)
, Z
(
t
0
)
}
(2.1.)
и њена брзина
V
(
t
0
)
={
V
X
(
t
0
)
,V
Y
(
t
0
)
,V
Z
(
t
0
)
}
(2.2.)
координате тачке у епохи опажања
t
могу се израчунати по формули:
X
(
t
)=
{
X
(
t
0
)
,Y
(
t
0
)
, Z
(
t
0
)
}
=
X
(
t
0
)
+
V
(
t
0
)
(
t
−
t
0
)
(2.3.)
Постоји више реализација ITRF са називима ITRF88, ITRF89, . . . , ITRF2014,
респективно. Свака од њих представља унапређење у односу на претходну у смислу
броја укључених станица и периода опажања са циљем добијања поузданих
вредности координата и брзина тачака.
Између различитих реализација ITRFyy могућа је седмопараметарска
трансформација сличности:
(
X
Y
Z
)
2
=
(
X
Y
Z
)
1
+
(
T
X
T
Y
T
Z
)
+
(
D
−
R
Z
R
Y
R
Z
D
−
R
X
−
R
Y
R
X
D
)
(
X
Y
Z
)
1
(2.4.)
где су:
-
T
X
,T
Y
,T
Z
параметри транслације по кореспондентним координатним осама,
-
R
X
, R
Y
, R
Z
параметри ротације око кооресподентних координатних оса
-
D
параметар размере
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
9
2.2. Светски геодетски систем 1984
Када се терестричком референтном систему придружи обртни елипсоид са центром
у координатном почетку, тачке на физичкој површи Земље се могу изразити у
елипсоидним (геодетским) координатама (геодетска дужина В, геодетска ширина L,
и елипсоидна висина h). Референтни елипсоид придружен ITRS дефинисан је
Геодетским референтним системом 1980 (Geodetic Reference System 1980,
GRS80).
Уз незнатне корекције GRS80 је 1984. године преиначен у Светски геодетски
систем WGS84 (World Geodetic Sysem 1984). WGS84 је назив елипсоида који се
користи као референтни координатни систем. Настао је модификовањем Поморског
навигационог сателитског система (NNSS) или TRANSIT и Доплеровог
референтног оквира (NSWC 9Z-2) у координатном почетку и размери, и ротирањем
до поклапања референтног меридијана са BIH нултим меридијаном.
Слика 2.4.
Однос елипсоида GRS80 и WGS84, приближно 2 m од геоцентра
WGS84 је геоцентрични координатни систем чији је центар у средишту масе
Земље, док су координатне осе дефинисане тако да је:
-
Z
– оса усмерена према средњем положају Северног пола СТР (Conventional
Terrestrial Pole) од 1900. до 1905. за поларно кретање,
-
X
– оса у пресеку равни нултог референтног меридијана координатног система
WGS84 и равни екватора,
-
Y
– оса 90Š источно од Х осе, формира десно орјентисан геоцентричан и
геофиксиран ортогонални координатни систем мерен у равни екватора.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
11
Одређивање такође укључује ласерско мерење дужина до ГЛОНАСС и ЕТАЛОН
(ЭТАЛОН) сателита. Подскуп ових станица користи се за емитовање ПЗ90
ГЛОНАСС сателитских орбита.
Кроз различите опажачке кампање (н. пр. IGEX
98) између референтних система
ПЗ90 и WGS84 одређени су прецизни параметри тродимензионалне
трансформације сличности, тако да је могуће користити податке опажања
ГЛОНАСС сателита заједно са GPS сателитима и циљу прецизног позиционирања
терестричких тачака (
Boucherи Altamimi
2001).
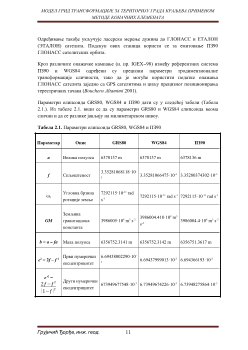
Параметри елипсоида GRS80, WGS84 и ПЗ90 дати су у следећој табели (Табела
2.1.). Из табеле 2.1. види се да су параметри GRS80 и WGS84 елипсоида веома
слични и да се разлике јављају на милиметарском нивоу.
Табела 2.1.
Параметри елипсоида GRS80, WGS84 и ПЗ90
Параметар
Опис
GRS80
WGS84
ПЗ90
a
Велика полуоса
6378137 m
6378137 m
6378136 m
f
Спљоштеност
3.35281068118·10
-
3
3.35281066475·10
-3
3.35280374302·10
-3
w
z
Угловна брзина
ротације земље
7292115·10
-11
rad
s
-1
7292115·10
-11
rad s
-1
7292115·10
-11
rad s
-1
GM
Земљина
гравитациона
константа
3986005·10
8
m
3
s
-2
3986004.418·10
8
m
3
s
-2
3986004.4·10
8
m
3
s
-2
b
=
a
fa
Мала полуоса
6356752.3141
m
6356752.3142
m
6356751.3617
m
e
2
= 2
f
–
f
2
Први нумерички
ексцентрицитет
6.69438002290·10
-
3
6.69437999013·10
-3
6.694366193·10
-3
e’
2
=
2
f
−
f
2
(
1
−
f
)
2
Други нумерички
ексцентрицитет
673949677548·10
-3
6.73949674226·10
-3
6.73948275864·10
-3
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
12
3. ЕВРОПСKИ ТЕРЕСТРИЧКИ РЕФЕРЕНТНИ СИСТЕМ
За могућност коришћења сателитског позиционирања, неопходна је реализација
глобалног терестричког референтног система (референтни оквир). Координате
сателита потребне за позиционирање морају бити представљене у кохерентном и
прецизном глобалном координатном оквиру. У најнапреднијем глобалном
глобалном терестричком референтном оквиру морају узети у обзир и промену
Земље, кретање тектонских плоча на годишњем нивоу, пост – глацијални
земљотреси, који мењају положај фиксних тачака.
Године 1987. International Association of Geodesy-IAG i CERCO (Comite Europeen
des Responsables de la Cartographie Officielle) одлучили су да развију нови Европски
референтни оквир EUREF, базиран на GPS технологији. То је требао да буде
прецизан и модеран систем, као WGS84 систем, који ће омогућити да се за
међународне дигиталне картографске податке као изворне користе бројни
национални датуми широм Европе.
Пошто је крајем 80-тих година прошлог века ITRS (International Terrestrial Reference
System) био најпрецизнији глобални референтни систем који је био доступан,
EUREF је одлучио да базира свој референтни систем на ITRS-у, којег одржава
Међународни сервис за Земљину ротацију и референтне системе IERS (International
Earth Rotation and Reference Systems Service). Међутим, у глобалном ITRS-у,
тектонски покрети континенталних плоча узрокују померања европских станица,
реда величине око 2,5 cm годишње.
Слика 3.1.
EUREF перманентне GPS станице
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
14
Ове препоруке значе да је ETRS89 постао “де факто” стандард Европске уније и да
је развој модела трансформације између националних референтних система и
ETRS89 постао ургентна потреба.
3.1. Имплементација ETRS89 референтног система
Систем ETRS89 имплементиран је на основу трансформационог модела (обрасци и
параметри) из ITRFii референтног оквира (ITRS система) у ETRFii референтни
оквир.
X
ETR F
yy
(
t
c
)
=
X
ITR F
yy
(
t
c
)
+
T
yy
+
[
0
−
R
3
yy
R
2
yy
R
3
yy
0
−
R
1
yy
−
R
2
yy
R
1
yy
0
]
X
ITR F
yy
(
t
c
)(
t
c
−
1989.0
)
;
(3.1.)
Формуле за конверзију укључују шест параметара: три транслације (
T
X
,T
Y
,T
Z
)
, и
три параметра ротације
R
X
, R
Y
, R
Z
. Параметри брзине ротације описују кретање
евроазијске континенталне плоче у глобалном референтном оквиру ITRFii и
користе се за пренос координата у ETRS89 као и што је дефинисано у односу на
епоху 1989.0., исправљањем кретања евроазијске континенталне плоче током
времена.
Параметри трансформације узимају у обзир разлике између различитих ITRFii
оквира. Формуле за конверзију дефинишу параметре (почетак, орјентацију и
размеру) референтног оквира ETRFii и као резултат тога, елиминише се временска
зависност ETRS89 и минимизирају се промене координата проузроковане кретањем
евроазијске кониненталне плоче.
Трансформација је одређена Европском перманентном мрежом GNSS станица (EPN
– EUREF Permanent GNSS Network). Положаји (и брзине кретања) станица у EPN
мрежи прво се израчунавају у глобалном ITRF
ii
референтном оквиру из којег се
њихове координате конвертују у одговарајући ETRF
ii
оквир.
До ITRF2000, за сваку нову реализацију ITRF
ii
одређени су нови параметри
трансформације за ETRS89, што је резултирало новом реализацијом система
ETRS89 – референтни оквир ETRFii, где је ii одговарајући ITRFii идентификатор
реализације.
Међутим, тако добијени ETRFii оквири се незнатно разликују због раазлике у
иплементацији ITRFii. Стога је, у својим резолуцијама из 2010. године, EUREF
комисија одлучила да препоручи ETRF2000 као конвенционални референтни оквир
за ETRS89 како би се смањиле разлике између различитих ETRFii оквира.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
15
Тако од ITRF2005, пут конверзије пролази кроз ITRF2000 до ETRF2000.
Резултирајућа листа координата EUREF Техничка радна група препоручује
позивање ETRF2000 (
R
ii
), где се крајњи параметар
R
ii
односи на ITRFii решење из
које је ова координатна листа генерисана. Слично томе, могуће је пребацивање са
било ког ITRFii на двостепену конверзију у друге ETRFii оквире. Везе између ITRS
и имплементација ETRS89 приказане су на слици (Слика 3.2.).
Слика 3.2.
Имплементација система ETRS89 помоћу ITRFii оквира
3.2. Перманентне GNSS мреже
Реализација ITRS-a заснована је на GNSS опажањима. У ову сврху користе се
перманентне GNSS опажачке станице широм света. Ове станице део су глобалне
или регионалних GNSS мрежа.
Ради прикупљања и анализе GNSS опажања, од стране IUGG-a (International Union
of Geodesy and Geophysics), 1994. године формирана је
Међународна GNSS
служба
(International GNSS Service).
Основни задатак IGS је да учини доступним неопходне податке за високотачне
геодетске и геофизичке примене коришћењем GNSS. У овом тренутку IGS обухвата
глобално распоређене перманентне станице (Слика 3.3.) и анализационе центре на
којима се врше опажања и обрада података GPS односно GPS и GLONASS система,
са планом да укључи и будуће видове GNSS.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
17
- регионални центри за прикупљање података,
- локални центри за прикупљање података,
- перманентне GNSS станице,
Основни задатак и циљ ове организације је дефинисање и одржавање референтног
система ETRS89 са својим производима, референтним оквирима. EPN организације
је одговорна за реализацију референтних оквира на територији Европе. Примарни
циљ је да се обезбеди хомогеност координата у целој Европи. Хомогеност
координата је главни проблем због сталног увећања количине GIS података и
неопходности њихове инетроперабилности и размене између европских држава.
EPN представља референтну научно истраживачку основу састављену од 266
континуално оперативних GNSS станица за праћење, чије се прецизне координате
срачунате на недељном нивоу, користе од стране EUREF поткомисије Међународне
геодетске асоцијације (IAG) за потребе реализације и одржавања ETRS89. Сви
доприноси EPN мрежи су на добровољној основи, при чему је у сам пројекат GNSS
глобализације укључено више од 100 европских агенција института и универзитета,
које гарантују квлаитет како сирових тако и резултујућих позиција базних станица.
Од 1997. године EPN доставља решења за координате и брзине тачака IERS у циљу
доприноса ITRFyy реализацијама. Као резултат, EPN станице укључене су у
ITRF97, ITRF2000 и ITRF2005 и формирају европски део “примарних” ITRS
референтних станица. Такође, урачунавањем ротације европске тектонске плоче од
1989. године, EPN станице формирају “примарну” ETRS89 мрежу.
Слика 3.4.
Европска перманентна мрежа
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
18
4. РЕАЛИЗАЦИЈА ETRS89 У СРБИЈИ
4.1. EUREF мерна кампања Балкан '98
Од стране Европског референтног оквира (
European Reference Frame –
EUREF)
1998. године реализована је мерна кампања
Балкан '98
када је Србија званично
укључена у европску референтну мрежу.
На територији Србије утврђено је 7 тачака, једна од тачака је на граници Србије са
Црном Гором. За тачке YUREF-а (Југословенски референтни оквир) изабрано је 7
тачака Тригонометријске мреже првог реда. Референтна мрежа Републике Србије се
ослања на југословенски референтни оквир.
Мерења су извршена у периоду од 4. септембра до 9. септембра 1998. године
применом GPS-а. На свим станицама је извршено 5 мерних сесија, које су трајале
по 24 сата са интервалом за регистрацију података од 15 секунди.
Обраду података је извршила Државна управа за геодезију и картографију Савезне
Републике Немачке у Франкфурту. При обради је коришћен софтвер
Bernese 4.0.
Слика 4.1.
Диспозиција тачака EUREF кампање Балкан '98 (Altiner и др 1999.)
Мрежа је дефинисана са неколико станица Европске перманентне мреже (
European
Permanent Network
- EPN) у систему ITRF96 (
International Reference Frame 1996
),
98,7 епоха. Резултат су биле координате новоутврђених тачака у систему ITRF96,
98,7 епоха.Стандардна девијација координата утврђених у оквиру кампање била је
2 mm, за хоризонталну компоненту, а 6.5 mm за висинску компоненту. Због
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
20
Републике Србије) и 7 тачака успостављених у оквиру македонске EUREF кампање
из 1996. године.
За дефиницију датума коришћене су искључиво тачке које су у систему Европске
мреже перманентних станица и то искључиво оне тачке које имају тачност од 1cm
(класе А) усистему координата ETRS89 и брзинама координатаодређним с
тачношћу од 1mm по години и то за сваку епоху.
Тако је изабрано 20 тачака које су најближе Републици Србији и испуњавају овај
услов. Ипак за дефиницију геодетског датума је искоришћено њих 18 јер је на две
станице промењена геодетска опрема и забележен је скок у њиховим резултатима.
Мерења са ове две тачке су ипак укључена у изравнање.
Слика 4.2.
Диспозиција EPN тачака класе А у кампањи EUREF СРБИЈА 2010
Интервал мерења је био 5 недеља, од 1. августа 2010. (213. дан у години, GPS
недеља/дан 1595/0) до 4. септембра 2010. године (247. дан у години, GPS
недеља/дан1599/6). Интервал мерења тачака на терену био је 3-5дана у сесијама од
24 часа у току 1597. GPS недеље. Изузетак је тачка Е803 у Македонији за коју
постоје мерења која су одбачена у току обраде података због лошег квалитета тако
да у коначном решењу ова тачка партиципира са опажањима од само два дана.
EPN станице класе А су коришћене за дефиницију геодетског датума у
референтном оквиру ITRF2005. Координате ових EPN станица преузете су из
последњег доступног кумулативног решења у време рачунања у SINEX формату
(Software Independent Exchange Format– Софтверски независан формат за размену
података). Просторни распоред ових станица дат је на
Слици 4.2
..
Комплетна математичка обрада GPS мерења извршенаје програмским пакетом
BerneseSoftware, version 5.0. Release 18-February-2010 и то у свему према упутству
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
21
који је издала техничка радна група EUREF-а и доступно је на официјелном
интернетпорталу EPN-а под насловом „
Guidelines for EPN Analysis Centers
“.
Оцењене координате EPN перманентних станица из финалног комбинованог
решења су поређене са координатама EPN перманентних станица из последњег
доступног кумулативног решења EPN_A_ITRF2005_C1600.SNX – Слика 4.3.
Слика 4.3.
Разлике у координатама EPN перманетних станица по латитуди и лонгитуди
Разлике у координатама EPN перманентних станица (Слика 4.3.) указују да је
реализација референтног оквира ITRF-2005-EUREF кампањом у Србији 2010.
године реализована са тачношћу од око 2 mm за све три координатне осе.
EUREF кампања у Србији 2010 године је прихваћена као денсификација Европског
референтног оквирау класи Б.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
23
првог реда, која се састојала од 595 углова.ТМ1 је повезана са триангулацијама
првог реда суседних земаља - Албаније, Бугарске, Грчке, Италије и Румуније.
Тригонометријска мрежа првог реда (ТМ1) на територији Републике Србије
представља основну или државну тригонометријску мрежу. Мрежни датум је
дефинисан на зони 7 Бесселовог елипсоида, а сва мерења су извршена између 1921.
и 1923. Мрежа се састоји од 130 тачака, а растојања између тачака су око 35 km
(Слика 2.1.). У мрежи је извршено мерење 672 праваца, а дужине су мерене
инварским жицама индиректно. Мрежа је изравната по деловима методом најмањих
квадрата, са просечном грешком правца од 0 ".80.
Слика 5.2.
Тригонометријска мрежа првог реда
Заједно са ТМ1, како је речено раније, у Србији су развијане и тригонометријске
мреже другог, трећег и четвртог реда, као и низ градских тригонометријских мрежа.
Слика 5.3.
Шема хијерархије тригонометријске мреж
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
24
Табела 5.1.
Уобичајена растојања између тригонометријских тачака
Ред тригонометријске мреже
Растојање
први ред
преко 20 km
други основни ред
15 km
20 km
други попуњавајући ред
9 km
19 km
трећи основни ред
5 km
13 km
трећи попуњавајући ред
3 km
7 km
четврти ред
1 km
4 km
Поред 162 тачке тригонометријске мреже првог реда, државна тригонометријска
мрежа Србије састоји се од 719 тачака другог реда и 57247 тачака трећег и четвртог
реда.
5.2. Гаус – Кригерова пројекција
Од 1924. године, у Србији је у употреби Беселов елипсоид као референтни
елипсоид, односно димензије двоосног обртног елипсоида који је мерењима од
1831. до 1838. године одредио немачки научник
Vilhelm Fridrih Besel
. Исте године
одлуком стручне комисије од стране владе Краљевине Југославије положајне
координате терестричких тачака у Државном координатном систему изражавају се
у конформној Гаус – Кригеровој пројекцији меридијанских зона, где је ширина зоне
по геодетској дужини Беселовог елипсоида
3
Основа Гаус – Кригерове пројекције је да се већи делови Земљине површи
пројектују на омотач једног замишљеног цилиндра, чија је узужна оса управна на
обртну осу планете Земље, тако да он стоји попречно у односу на њу . Због тога се
ова пројекција зове Гаус – Кригерова попречно цилиндрична пројекција
меридијанских зона. (Слика 5.2.)
Слика 5.4.
Гаус – Кригерова пројекција
Кад се омотач цилиндра расече по равни који садржи екватор (по изводници
цилиндра) и развије у раван, добија се пројекциона раван на коју је могуће
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
26
Где су
f
Y
GK
,
f
X
GK
једначине Гаус – Кригерове пројекције а
a , f
параметри (велика
полуоса и спљоштеност) земљиног елипсоида.
Слика 5.6.
Положајне координате у Гаус – Кригеровој пројекцији
Координата
X
T
представља растојање тачке од екватора, у равни пројекције и
позитивна је од екватора према северу а негативна од екватора према југу.
Координата
Y
T
представља растојање тачке од централног меридијана, у равни
пројекције и позиивна је од централног меридијана према истоку а негативна од
централног меридијана према западу. Пар координата за произвољну тачку
T
(
Y
T
, X
T
)
дефинише се као координате у равни Гаус – Кригерове пројекције
додирног цилиндра или немодулисано координате.
Пошто пројекциони цилиндар додирије елипсоид по централном меридијану
(додирни цилиндар) он се пресликава на цилиндар као права без деформација,
односно у размери
k
0
=
1
што значи да је његова дужина иста као на елипсоиду.
Међутим, све дужине ван додирног меридијана биће деформисане. Дуж линија
параленим са
X
осом, односно геометријског места тачака са константном
вредношћу координате
Y
размера дужине износи
k
=
k
0
+
Y
2
2
R
2
+
4
Y
2
2
R
2
+
…
(5.4.)
где је
R
=
√
M
(
φ
)
N
(
φ
)
(5.5.)
средњи полупречник закривљености елипсоида на геодетској ширини φ, где се за
Беселов елипсоид и целу територију Србије са довољном тачношћу може узети
јединствена вредност
R ≈
6377
km .
У практичним применама израз (5.4.) може се
ограничити само на први члан па се коефицијент размере може рачунати као
k
≅
k
0
+
Y
2
2
R
2
(5.6.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
27
Коефицијент размере за дужине
k
расте са удаљавањем од централног меридијана
према изразу (5.4.) и за додирни цилиндар, већ за
Y
=
90.18
km
деформација дужине
W
=
k
−
1
=
Y
2
2
R
2
−
(
1
−
k
0
)
,
(5.7.)
достиже
W
=
1
dm
/
km
. У циљу оптимизације вредности деформација дужине у
оквиру координатне зоне за коефицијент размере на централном меридијану ставља
се
k
0
=
0.9999
,
чиме се постиже пресликавање површи елипсоида на цилиндар чији
је радијус умањен за коефицијент размере
k
0
и који пресеца елипсоид на растојању
≈
90.18
km
од централног меридијана – секући цилиндар.
Координате произвољне тачке Т на елипсоиду у дводимензионалном декартовом
систему Гаус – Кригерове пројекције на секући цилиндар – модулисане координате
могу се онда добити као:
Y
T
=
Y k
0
+
500000
+
n
Z
1000000
(5.8.)
X
T
=
X k
0
(5.9.)
Константа 500000 додаје се да би се избегле негативне вредности за координату
Y
а
додавањем вредности
n
Z
1000000
постиже се да прва цифра координате
Y
означава
број координатне зоне.
Деформације дужина дуж централног меридијана имају вредност
W
=−
1
dm
/
km
, на
линијама пресека пројекционог цилиндра са земљиним елипсоидом једнаке су нули
и позитивне западно и источно од појаса који формирају линије пресека
пројекционог цилиндра са земљиним елипсоидом.
Слика 5.7.
Гаус – Кригерова пројекција – дијаграм размере дужина у функцији средње
координате
Y
m
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
29
5.3.1. Основна просторна референтна мрежа EUREF - SRBIJA
Основну просторну референтну мрежу чини скуп од 12 трајно стабилизованих и
приступачних геодетских тачака, равномернораспоређених по територији
републике Србије на просечном међусобном растојању од 100 km,
- пет тачака тригонометријске мреже првог реда
- једна тачка оскултационе мреже бране ''Ћелије''
- шест тачака просторне референтне мреже.
Најнижа тачност релативног хоризонталног положаја тачака основне просторне
мреже мора бити 5 mm+1 ppm, а релаtивног положаја 10 mm + 1ppm.
Мерења у основној просторној референтној мрежи Републике Србије изводе се
мерним инструментима и методама сателитске геодезије.Мерења и обрада података
се изводе се сваких пет година у цињу осигурања интегритета и праћења временске
еволуције просторног координатног референтног система. Реализација ове мреже
шире је описана у поглављу 4.
5.3.2. Активна геодетска референтна основа Србије – АГРОС
Од децембра 2005. године Републички геодеткси завод (РГЗ) у сарадњи са
Факултетом техничких наука у Новом Саду успоставио је мрежу сталних станица
Србије под називом Активна геодетска референтна основа Србије (АГРОС) (Слике
2.7.а/б.). Мрежа у складу са пројектом створеном у периоду од 2001. до 2003.
године требало је да садржи: два контролна центра, 34 сталне станице и 3
корисничка центра. Међутим, ситуација у Србији тог времена, као и ниво развоја
телекомуникационих мрежа, омогућила је реализацију пројекта само делимично.
У децембру 2005. године успостављена је мрежа са укупно 30 станица, 1
контролним центром у Новом Саду и потпуно успостављеним РТК и ДГПС
(
Differential Global Positioning System
) системом заснованим на концепту VRS-а
(
Virtual Reference Station
). Услуга за накнадну обраду (post processing) је
успостављена само делимично: корисник је могао преузети податке за накнадну
обраду, али такође није могао коначно да их обради користећи ресурсе АГРОС-а.
Према томе, АГРОС је систем који чине:
- перманентне станице
- контролни центар за пријем, обраду и дистрибуцију података.
Од тренутка успостављања АГРОС је стално био у употреби али и континуирано се
мењала организација рада система, као и дистрибуција станица. Говорећи о
промени организације система рада, најзначајнија је била промена локације
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
30
контролног центра, из Новог Сада у Београд, као и чињеница да у овом тренутку
РГЗ самостално води све сегменте АГРОС-а, док се конфигурација мреже мењала
неколико пута. У северном делу АГРОС-а станица у Новом Саду била је одвојена
од мреже. Станица у Вршцу пребачена је у Пландиште и станица од Љига до
Горњег Милановца. Такође је примећено да станица у Краљеву функционише са
одређеним поремећајима и тренутно се изводе неки препаративни радови у циљу
евентуалног преноса станице на нову локацију.
Сли
ка 5.9.
Активна геодетска референтна основа Србије
5.3.3. Државна референтна мрежа
Републички геодетски завод је у периоду од 1998. до 2003. године планирао и
реализовао просторну референтну мрежу Републике Србије под називом Пасивна
геодеткса основа – SREF (Слика 5.10.).
Мрежа се састоји од укупно 838 стално стабилизованих тачака правилно
дистрибуираних по територији Републике Србије (искључујући Косово и Метохију)
са просечном просторном резолуцијом од 10 km.
Поред нових планираних тачака, тачке постојеће тригонометријске мреже су
укључене. Посебна пажња била је посвећена стабилизацији тачака, тако да оне могу
истовремено служити и као вертикални репери.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
32
Слика 5.11.
Начин стабилизације тачака државне референтне мреже
Нове тачке Државне референтне мреже стабилизују се стандардним типом белеге
тј. надземном бетонском белегом, стубом висине 30 cm, са уграђеном металном
болцном. У изузетним случајевима тачка се може стабилизовати и другачије.
У периоду од 2011 до 2012 године у Сектору за геодетске радове извршено је
рекогносцирање и стабилизација уништених тачака, мерење у рачунање Просторне
референтне мреже Републике Србије. Математичка обрада података вршена је у
циљу добијања дефинитивнох координата тачака референтне мреже и оцене
тачности извршених мерења и добијених резултата.
Извршена обрада података подразумева следеће целине:
- Обрада извршених GPS опажања, процесирање GPS вектора и затварање
полигона -
Прелиминарно процесирање GPS вектора вршено је непосредно
након извршених GPS мерења, по завршетку сваког опажачког дана. При обради
су употребљене комерцијалне ефемериде које су у саставу навигационе поруке.
Дефинитивно процесирање GPS вектора урађено је са прецизним ефемеридима.
Овим процесирањем GPS вектора добијене су вредности величина које се у
изравнању сматрају мереним величинама, са одговарајућом коваријационом
матрицом. Извршена мерења сматрана су квалитетним ако је незатварање
полигона састављених од 3 и више GPS вектора било мање од 3 ppm.
- Испитивање сагласности тачака референтне мреже и 12 тачака EUREF-
BLOKSRBIJA -
Испитивање сагласности извршено је Хелмертовом
трансформацијом 12 SREF тачака добијених из слободног изравнања, у
координате EUREF – BLOK SRBIJA. Ова трансформација је извршена као
контрола квалитета.
-
Одређивање координата тачака референтне мрежеу систему ЕTRS89 –
слободноизравнање мреже
- Изравнање државне референтне мреже вршено је
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
33
по методи најмањих квадрата и по начину посредних мерења са условима међу
непознатим мерењима.
-
Испитивање сагласности 814 тачака просторне референтне мреже статус
2011 и 814 тачака просторне референтне мреже статус 2012
- Испитивање
сагласности извршено је Хелмертовом трансформацијом 814 тачака SREF2011 и
SREF2012. Ова трансформација је извршена као контрола квалитета.
-
Одређивање координата тачака референтне мрежеу систему ЕTRS89 -
Изравнање државне референтне мреже вршено је по методи најмањих квадрата
и по начину посредних мерења са условима међу непознатим параметрима.
Поступак изравнања је обухватио једновремено изравнање свих процесираних
независних GPS вектора. Функционални део математичког модела дефинисан је
без допунских параметара, тако да су основне непознате параметре
представљали само прираштај координата. Датум мреже дефинишу координате
седам тачака YUREF мреже. Мерене величине у изравнању су координатне
разлике
Δx, Δy, Δz.
Изравнањем мреже референтних тачака добијене су
просторне правоугле координате
X,Y, Z
у ETRF2000 епоха 2010.631.
Из свега наведеног може се закључити да је Државна референтна мрежа кроз време
редовно одржавана, што се да и видети кроз три статуса од прве њене реализације.
У периоду од 2003 до 2012 године укупно је уништено 46 тачака које су поново
стабилизоване и измерене.
5.4. UTM пројекција
Законом о државном премеру и катастру из 2009. године донето је увођење
референтног система ETRS89 у Републици Србији и такође одређено да се
хоризонтални положај тачака изражава дводимензионалним, праволинијским
координатама у равни конформне Универзалне трансверзалне меркаторове
(Universal Transverse Mercator, UTM) пројекције елипсоида GRS80. UTM пројекција
представља модификацију Гаус-Кригерове пројекције, где је земљин елипсоид
подељен на 60 меридијански (координатних) зона, свака ширине 6Š по геодетској
дужини λ.
Конформне координате у равни пројекције произвољне терестричке тачке
T
(
E
T
, N
T
)
(Слика 5.12.) на додирном цилиндру, добијају се једначинама идентичним Гаус-
Кригеровој пројекцији, односно
Е
Т
=
Y
T
=
f
Y
GK
(
φ
T
, λ
T ,
a , f
)
(5.10.)
N
T
=
X
T
=
f
X
GK
(
φ
T
, λ
T ,
a , f
)
(5.11.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
35
k
≅
k
0
+
E
2
2
R
2
,
(5.14.)
где је
R
=
√
M
(
φ
)
N
(
φ
)
(5.15.)
средњи полупречник закривљености елипсоида на геодетској ширини
φ
, где се за
елипсоид GRS80 и целу ериторију Србије, са довољном тачношћу, може узети
јединствена вредност
R ≈
6378
km
.
Слика 5.13.
UTM пројекција – дијаграм размере дужина у функцији средње кооринате
E
m
Деформације дужина:
W
=
k
−
1
=
E
2
2
R
2
−(
1
−
k
0
)
(5.16.)
Дуж централног меридијана биће
W
=−
40
cm
km
, на растојању
±
180,40
km
источно и
западно од централног меридијана биће једнаке нули док ће на крајевима зона
највеће вредности имати на екватору
W ≈
+
98
cm
/
km
.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
36
Слика 5.14.
UTM пројекција -просторни распоред деформација дужина W =k - 1 у cm/km
Како су на територији Србије највеће удањености, од централног меридијана
λ
0
=
21
° E ,≈
169.4
km
према западу и
≈
162.9
km
према истоку деформације дужина W
имаће увек негативан предзнак и кретаће се у распону од
W = -40 cm/km
дуж
централног меридијана до
W ≈
0
cm
/
km
, на најзападнијој тачки државне границе
(Слика 5.14.).
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
38
6. МОДЕЛИ ТРАНСФОРМАЦИЈЕ ДАТУМА
Трансформација између геодетских датума је потребна из разлога што се просторни
подаци све више глобализују, док су модерне тхнике мерења (GNSS) у широку
употребу увеле глобалне геодетске датуме, чије су реализације пуно квалитетнија
(прецизнија) решења од локалних. Најчешће коришћене координате тачака су оне
које се односе на неки локани (референц) елиспоид, који дефинише датум локалног
(негеоцентричног) система, нпр. државни координатни систем или
дводимензионалне координате у равни картографске пројекције.
Уколико је потребно тачку из једног координатног система приказати у другом
координатном систему потребно је извршити датумску трансформацију. Датумска
трансформација конвертује координате тачке дате у координатном систему Датума
А у координате у координатном систему Датума Б (Слика 6.1.)
Слика 6.1.
Датумска трансформација
Ако две тачке из два различита координатна система имају придружену просторну
референцу, односно ако су познати пројекција са својим параметрима, елипсоид на
који се пројектује, као и однос према референтном координатном систему, могуће
је заједничко коришћење података.
Параметри датумске трансформације омогућују директан прелаз са WGS84 на
Беселов елипсоид, односно конвертовање координате тачке дате у WGS84 у
координате на Bessel 1841 елипсоиду (Гаус-Кругеров координатни систем).
Да би се ова два просторна координатна система (Е1 и Е2) поклопила потребно је
један од њих (Е2) ротирати око све три осе, променити му размеру и померити га у
простору (Слика 6.2.). Скуп параметара који дефинишу датумску трансформацију
називају се трансформациони параметри. За трансформацију је потребно познавати
седам параметара (3 транслације, 3 ротације и параметар размере), па се назива
седмопараметарска датумска трансформација или Хелмертова трансформација.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
39
Слика 6.2.
Седмопараметарска датумска трансформација
Са чисто математичке тачке гледишта неопходно је само 6 параметара. Међутим,
проблем настаје због нехомогености државног геодетксог система чије координате
улазе у трансформацију, због чега није могуће на територији комплетне државе
једнозначно одредити трансформационе параметре који би задовољавали геодетску
тачност. Због тога се параметри одређују унутар једног мањег подручја, где ће
нехомогеност мреже имати мањи или исти утицај на новоодређене тачке.
Трансформациони параметри добијени на овакав начин ће се значајно разликовати
од параметара у суседном подручју, што је свакао условљено локалним утицајима.
С друге стране проблем лежи у чињеници што је постојећа триангулацијска мрежа
дводимензионална, с лоше одређеном висинском компонентом док прецизна
висинска мрежа већином нема добре положајне координате. Из тог разлога се
трансформација датума код прецизних радова, не сме користити без употребе
геоида. Чак и када су висине добро одређене, утицај геоида у мрежама које имају
иоле веће протезање или садрже знатније варијације висина бити значајан.
У поступку трансформације координата тачака из једног у неки други координатни
систем могуће је применити различите трансформационе моделе. У односу на
величину подручја на коме се примењују трансформациони модели се могу
сврстати у једну од следећих група:
-
Глобални модели
. Ова група односи се на моделе који имају јединствену
структуру и број параметара на целој државној територији.
-
Локални модели
. Ови модели подразумевају јединствену структуру и број
параметара на ограниченим деловима државне територије и у овом раду се
називају коначним елементима. Локални модели по коначним елементима могу
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
41
Извођење ових формула приказано је у
Soler
1976,
Lеick и van Gelder
1975 и
Grafarend, Knickmeyer и Schaffrin
1982.
Матрица ротације
R
је ортогонална матрица која садржи три сукцесивне ротације
око сваке од координатних оса
R
R3
{}
R2
{}
R1
{}
,
(6.3.)
где су
R
1
{
α
}
=
[
1
0
0
0 cos
α
sin
α
0 - sin
α
cos
α
]
,
R
2
{
β
}
=
[
cos
β
0 - sin
β
0
1
0
sin
β
0 cos
β
]
(6.4.)
R
3
{
γ
}
=
[
cos
γ
sin
γ
0
- sin
γ
cos
γ
0
0
0
1
]
,
односно
R
=
[
cos
β
cos
γ
cos
α
sin
γ
+
sin
α
sin
β
cos
γ
sin
α
sin
γ
−
cos
α
sin
β
cos
γ
−
cos
β
sin
γ
cos
α
cos
γ
−
sin
α
sin
β
sin
γ
sin
α
cos
γ
+
cos
α
sin
β
sin
γ
sin
β
−
sin
α
cos
β
cos
α
cos
β
]
(6.5.)
За случај трансформације између глобалног и Државног координатног система
премера непокретности у Србији (локалног) углови ротације
,
и
су мали (реда
величине неколико лучних секунди), па се матрица ротације
R
може написати у
поједностављеном облику
R
=
[
1
γ
−
β
−
γ
1
α
β
−
α
1
]
(6.6.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
42
Имајући у виду да је параметар размере
s
такође мала величина (реда 10
-5
), израз
(6.2.) са довољном тачношћу може се написати као
[
X
L
−
X
G
Y
L
−
Y
G
Z
L
−
Z
G
]
=
[
1 0 0
0
−
Z
G
Y
G
X
G
0 1 0
Z
G
0
−
X
G
Y
G
0 0 1
−
Y
G
X
G
0
Z
G
]
[
t
x
t
y
t
z
α
β
γ
s
]
(6.7.)
односно, у матричном облику
l = Ax,
(6.8.)
где је
l
,
n
димензионални вектор резултата мерења,
А
,
n
7, матрица једначина
везе и
x
вектор непознатих параметара. Да би се оценили параметри
трансформације неопходно је најмање три идентичне тачке. У пракси је број
идентичних тачака обично већи па се параметри трансформације одређују кроз
изравнање по методи најмањих квадрата. Према томе, оцене параметара
трансформације могу се добити као
^
x
=
[
^
t
x
^
t
y
^
t
z
^
α
^
β
^
γ
^
s
]
=
(
A
T
A
)
−
1
A
T
l
(6.9.)
при чему се подразумева да је матрица тежина резултата мерења јединична матрица
(
P
X
L
,Y
L
, Z
L
=
I
). Коваријациона матрица непознатих параметара добија се из израза
K
^
x
^
x
=s
0
2
(
A
T
A
)
−
1
(6.10.)
где је
s
0
2
експериментална референтна варијанса
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
44
У случају позантих параметара трансформација тачка из
X
GPS
може се
трансформисати у
X
DKS
помоћу једначине (7.5.1). Међутим ако су параметри
трансформације непознати, они могу бити одређени помоћу идентиних тачака у оба
координатна система. Математички гледана најмање две тачке су довољне за
одређивање четири непознате, уколико их има више потребно је користити метод
најмањих квадрата.
Уводећи помоћне величине имамо:
p
=
μ
cos
α
q
=
μ
sin
α
(6.16.)
Слика 6.4.
Дводимензионална трансформација сличности
Уврштавањем
p
и
q
у израд (6.15.) добијамо:
X
DKS
=
c
1
+
p X
GPS
−
q Y
GPS
Y
DKS
=
c
2
+
p X
GPS
−
q Y
GPS
(6.17.)
У случају више заједничких тачака, до решења долазимо применом петоде
најмањих квадрата, па имамо следеће једначине поправака:
ν
xi
=
c
1
+
X
GP S
i
p
−
Y
GP S
i
p
−
X
DKS
ν
yi
=
c
2
+
X
GP S
i
p
−
X
GP S
i
q
−
Y
DKS
(6.18.)
Тј. у матричном облку:
ν
=
Adx
−
l
(6.19.)
где је:
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
45
A
i
=
[
1
0
0
1
X
GPSi
Y
GPSi
−
Y
GPSi
X
GPSi
]
dx
=
[
c
1
, c
2
, p , g
]
T
(6.20.)
l
=
[
X
DKS
Y
DKS
]
Нормалне једначине, решење нормалних једначина и добијање параметара
трансформације тј. вектора непознатих x, рачунање поправака и провођење
потребних контрола дато је у матричном облику:
N
=
A
'
A ,Q
=
N
−
¿
,
−
n
=−
A
'
l , x
=
nQ
¿
(6.21.)
Рашавањем нормалних једначина добија се матрица
n
:
A
;'
l
=
n
=
[
Y
GPS
Y
DKS
X
GPS
Y
DKS
Y
DKS
X
DKS
+
−
X
GPS
X
DKS
Y
GPS
X
DKS
]
(6.22.)
Контрола изједначења:
ν
'
ν
=−
l
'
ν
(6.23.)
Наведене формуле важе за једну тачку. Уколико имамо
n
идентичних тачака,
вектори
v
и
l
, те матрица коефицијената
А
гласи:
ν
=
¿
(6.24.)
Из нумеричких разлога препоручљива је редукција координата увођењем тежишта,
за оба координатна система. Тежиште система изражавамо као средњу вредност
координата:
X
DKSs
=
X
DKS
n
,Y
DKSs
=
Y
DKS
n
X
GPSs
=
X
GPS
n
,Y
GPSs
=
Y
GPS
n
(6.25.)
где је
n
број тачака.
Свака поједина координата може бити изражена у систему тежишта:
X
DK S
novi
=
X
DK S
i
−
X
DK S
s
,Y
DK S
novi
=
Y
DK S
i
−
Y
DK S
s
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
47
За решавање дводимензионалне трансформације потребно је имати положајне
координате у оба система занемарујући елипсоидне и ортометријске висине
идентичних тачака. Редослед рачунања је следећи:
- На вредност картезијевих
(X,Y)
GPS
координата додаје се вектор транслације c
1
и c
2
чију је вредностдовољно познавати на неколико метара.
- Из добијених картезијевих координата рачунају се елипсоидне координате
(
ϕ
,
λ
)
GPS
при чему се користе параметри WGS84 елипсоида.
- Из елипсоиднх координата
(
ϕ
,
λ
)
GPS
рачунају се координате у равни
(x,y)
GPS
са
параметрима WGS елипсоида и у односу на 6
˚
меридијан.
- Из елипсоидних координата
(
ϕ
,
λ
)
DKS
рачунају се координате у равни
(x,y)
DKS
са
параметрима Беселовог елипсоида.
- Из идентичних тачака у оба координатна система рачунају се параметри
дводимензионалне трансформације.
- Са тако познатим параметрима можемо GPS координате трансформисати у DKS.
6.3. Грид трансформација
Једно од решења којим се значајно умањује утицај постојећих дисторзија јесте
модел трансформације са оцењивањем (предикцијом) вредности дисторзија
просторних података у тачкама правилног грида за одговарајуће изабрани интервал
(корак), на основу познатих вредности дисторзија у идентичним тачкама оцењеним
у поступку трансформације сличности.
Модел грид трансформације заснива се на конфорном помаку датума (Хелмертова
7-параметарска трансформација) коришћењем јединствених трансформационих
параметара и додатној транслацији дефинисаној на основу грид дисторзионог
модела (Слика 6.6.). Јединствени трансформациони параметри одређени су према
Bursa – Wolf алгоритму чије се једначине базирају на правоуглом геоцентричном
координатном систему.
Слика 6.6.
Хелмертова 7 – параметарска трансформација и модел дисторзије
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
48
Приказ поступка трансформавије између изворног и циљног координатног система
у познатом матричном облику гласи (
Hofman – Wellenhof и др., 1994
):
X
C
=
t
+
mR X
l
(6.30.)
где је:
-
X
C
– тродимензионални вектор координата у циљном систему
-
X
l
– тродимензионални вектор координата у изворном систему
-
t
– вектор транслације
-
m
– фактор размере
-
R
– матрица ротације.
Након примене Хелмертове просторне 7-параметарске трансформације добијене
трансформисане координате се додатно поправљају дисторзионим корекцијама
одређеним из јединственог грида кога представља четвороугаоно поље.
У овом поступку свако подручје на почетку мора бити дефинисано својим
границама у равни (
Y
min
−
X
min
)-(
Y
max
−
X
max
). Друга важна карактеристика ГРИД-а је
његова густоћа, односно број колона и редова решетке или размак између њених
колона и редова. Уколико је ГРИД декларисан на напред наведени начин тада ће
размак између колона и редова износити:
d
Y
=
Y
max
−
Y
min
n
Y
−
1
, d
X
=
X
max
−
X
min
n
X
−
1
(6.31.)
а уколикао декларација подразумева задате размаке у оба смера, тада ће број колона
и редова износити:
n
Y
=
Y
max
−
Y
min
d
Y
+
1
, n
X
=
X
max
−
X
min
d
X
+
1.
(6.32.)
Увећање за "1" у једначинама (6.32.), односно одузимање у имениоцима једначина
(6.31.) представља последицу чињенице да је број "жица" у решетки увек за један
већи од броја правоугаоника између две суседне "жице" по дужини неке од обеју
оса.
Аналогно томе било која произвољно изабрана тачка која се налази унутар граница
подручја ГРИД-а Т(
X ,Y
) положајно се индексира (референцира) на следећи начин:
i
=
Y
−
Y
min
d
Y
+
1
, j
=
X
−
X
min
d
X
+
1
;i , j
∈
N
(6.33.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
50
b
3
=
δ Y
1
+
δ Y
3
−
δ Y
2
−
δ Y
4
Док се вредности аргумената
X
и
Y
у истим једначинама одређују као:
X
=
X
P
−
X
1
X
2
−
X
1
Y
=
Y
P
−
Y
1
Y
2
−
Y
1
(6.36.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
51
7. МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ МЕТОДОМ КОНАЧНИХ
ЕЛЕМЕНАТА
Избор модела трансформације код просторних података између локалног и
глобалног референтног система зависи од основног критеријума –
тачност и
поузданост изворних података
. Критеријум се може остварити коришћењем
конформне трансформације. Тако се за трансформацију просторних података
прикупљених применом GNSS (Активне геодетске референтне основе) најчешће
користи седмопараметарска трансформација сличности описана у подпоглављу 6.2.
Коришћењем ове трансформације просторни подаци се транслирају, ротирају и
мења им се размера при чему облик остаје очуван, тј. не долази до промене у
просторној тачности.
Међутим, проблем трансформације просторних података из глобалног геодетског
референтног система у локални и обрнуто, постаје много сложенији ако постоји
присуство
дисторзија
(изобличења) просторних података изражених у локалном
геодетском референтном систему. За дисторзију се може рећи да представља модел
промене облика трансформисане мреже тачака који настаје због различитих износа
и орјентације резидуала – координатних поправака између почетног и циљног
координатног система на различитим локацијама.
Разлог за појаву ових дисторзија, у првом реду, је слаба условљеност геодетског
референтног оквира реализованог терестричким техникама (
Jäger и др.
2003).
Као
резултат
јавља
се
велика
зависност
релативне
тачности просторног положаја тачака изражених у локалном геодетском
референтном систему од растојања између тачака. Због тога је неопходно да се у
процесу трансформације постојеће дисторзије значајно умање или ако је могуће и
потпуно отклоне. Са аспекта корисника решење овог проблема представља модел
трансформације кога карактеришу једноставност, ефикасност, јединственост и
тачност.
Најпопуларнији интуитивно најјаснији начин моделирања дисторзије, као и сваке
потенцијалне физичке површи јесте решеткасти модел –
енгл. GRID
, док се
топографске карактеристике терена у пракси најчешће моделирају мрежом
троуглова –
енгл. TIN (Triangulated Irregular Network).
У првом случају захтевани
математички процес је интерполација дискретних вредности чворова решетке, а у
другом повезивање мреже троуглова према приниципу Delaunay-eve триангулације
– што значи да ни једна троуглу суседна тачка не сме бити унутар његове описане
кружнице
(Voronoi, 1908; Delanuay, 1934).
У пракси се за моделирање дисторзије обично користе следеће методе:
- Површ минималне закривљености (Minimum Curvature Surfaces-MCS);
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
53
На основу скупова геодетских координата у глобалном геодетском референтном
систему (
X
GRS
,
Y
GRS
,
Z
GRS
) и Државном координатном систему (
X
DKS
,
Y
DKS
,
Z
DKS
), за
n
t
(
i
)
(
n
t
(
i
)
3) идентичних тачака у оквиру
i
тог елемента (
i
= 1, 2, . . .,
n
e
), могуће је
добити оцену параметара тродимензионалне трансформације сличности
^
x
(
i
)
, као
^
x
(
i
)
=−
{
[
A
(
i
)
]
T
P
(
i
)
A
(
i
)
}
−
1
[
A
(
i
)
]
T
P
(
i
)
l
(
i
)
,
(7.1.)
са кореспондентном коваријационом матрицом
K
^
x
^
x
(
i
)
=
(
s
0
(
i
)
)
2
[
(
A
(
i
)
)
T
P
(
i
)
A
(
i
)
]
−
1
,
(7.2.)
где је
s
0
(
i
)
експериментална референтна варијанса за
i
ти елеменат
(
s
0
(
i
)
)
2
=
(
l
(
i
)
−
A
(
i
)
^
x
(
i
)
)
T
P
(
i
)
(
l
(
i
)
−
A
^
x
(
i
)
)
3
n
t
(
i
)
−
7
,
(7.3.)
при чему се подразумева да су, за свих
n
t
(
i
)
идентичних тачака, поред положајних
геодетских координата у Државном координатном систему (
X
j
(
i
)
)
DKS
, (
Y
j
(
i
)
)
DKS
,
познате и елипсоидне висине (
h
j
(
i
)
)
DKS
, (
j
= 1, 2, . . . ,
n
t
(
i
)
). Ово је могуће, обзиром да
је, при разматрању само положајног проблема, довољно познавати апроксимативне
вредности елипсоидних висина (
h
j
(
i
)
)
DKS
. Такође, параметри глобалног елипсоида
GRS80 као и локалног Bessel
овoг елипсоида су познати, тако да разлике
параметара елипсоида у процесу тродимензионалне трансформације сличности није
потребно оцењивати.
Применом параметара дводимензионалне трансформације сличности
x
(
i
)
добијају се
вредности оцењених (трансформисаних) координата свих тачака у оквиру
i
тог
елемента (
^
X
j
(
i
)
)
DKS
, (
^
Y
j
(
i
)
)
DKS
. Оцена тачности (коваријациона матрица) ових
координата може се добити из израза
K
^
B ,
^
L
(
i
)
=
A
(
i
)
K
^
x
^
x
(
i
)
(
A
(
i
)
)
T
.
(7.4.)
Уколико су подручја коначних елемената довољно мала онда се резидуали
(одступања)
v
X
j
(
i
)
=
(
X
j
(
i
)
)
DKS
−
(
^
X
j
(
i
)
)
DKS
v
L
j
(
i
)
=
(
Y
j
(
i
)
)
DKS
−
(
^
Y
j
(
i
)
)
DKS
,
i
= 1, 2, . . . ,
n
e
,
j
= 1, 2, . . . ,
n
t
(
i
)
,
(7.5.)
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
54
на
n
t
(
i
)
идентичних тачака
i
тог елемента могу сматрати чисто случајним
величинама, односно подразумева се да су она резултат искључиво присуства
случајних грешака у координатама тачака узорка просторних података.
Примена засебних параметара дводимензионалне трансформације сличности за
сваки елеменат
^
x
(
i
)
(
i
= 1,
. . .
,
n
е
) доводи до вишезначних решења за позиције
тачака чворова, односно за сваку од
n
c
тачака чворова, добија се онолико решења
колико и елемената у чијем формирању појединачна тачка чвор учествује (Слика
7.2.). У циљу постизања континуитета између суседних елемената, за дефинитивне
(јединствене) вредности координата
k –
те тачке чвора може се тада усвојити:
~
X
DKS
k
=
∑
l
=
1
n
e
k
^
X
DKS
k
(
l
)
n
e
k
~
Y
DKS
k
=
∑
l
=
1
n
e
k
^
Y
DKS
k
(
l
)
n
e
k
,
k
= 1, . . . ,
n
c
.
(7.6.)
где
n
e
k
може бити минимално један а максимално четири, у зависности од броја
коначних елемената у чијем формирању свака појединачна тачка чвор учествује.
Слика 7.2.
Релативни односи коначних елемената после примене засебних параметара
трансформације x(i) по елементима
Услови континуитета подразумевају да се на сваки елеменат
i
примени додатна
дводимензионална трансформација тако да све тачке чворови које формирају
i
ти
елеменат добију вредности (7.6) као и да све тачке на граничним линијама суседних
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
56
^
y
DKS
1
(
i
)
,
^
x
DKS
1
(
i
)
,
^
y
DKS
2
(
i
)
,
^
x
DKS
2
(
i
)
,
^
y
DKS
3
(
i
)
,
^
x
DKS
3
(
i
)
,
^
y
DKS
4
(
i
)
,
^
x
DKS
4
(
i
)
,
као и кореспондентне вредности добијене осредњавањем (7.6) и изразима (7.7)
~
y
DKS
1
i
,
~
x
DKS
1
i
,
~
y
DKS
2
i
,
x
DKS
2
i
,
~
y
DKS
3
i
,
~
x
DKS
3
i
,
~
y
DKS
4
i
,
~
x
DKS
4
i
.
На ове скупове координата може се применити дводимензионална пројективна
трансформација између координата тачака чворова карактеристичних за
i
ти
елеменат и њихових вредности добијених осредњавањем између суседних
елемената. За сваку од четири тачке чвора, које формирају
i
ти елеменат, могу се
написати по две једначине пројективне трансформације
~
y
DKS
m
i
=
a
1
^
y
DKS
m
(
i
)
+
a
2
^
x
DKS
m
(
i
)
+
a
3
c
1
^
y
DKS
m
(
i
)
+
c
2
^
x
DKS
m
(
i
)
+
1
~
x
DKS
m
i
=
b
1
^
y
DKS
m
(
i
)
+
b
2
^
x
DKS
m
(
i
)
+
b
3
c
1
^
y
DKS
m
(
i
)
+
c
2
^
x
DKS
m
(
i
)
+
1
,
m
= 1, 2, 3, 4,
(7.8.)
односно
~
y
DKS
m
i
= ^
y
DKS
m
(
i
)
a
1
i
+ ^
x
DKS
m
(
i
)
a
2
i
+
a
3
i
− ^
y
DKS
m
(
i
)
~
y
DKS
m
i
c
1
i
−^
x
DKS
m
(
i
)
~
y
DKS
m
i
c
2
i
~
x
DKS
m
i
= ^
y
DKS
m
(
i
)
b
1
i
+ ^
x
DKS
m
(
i
)
b
2
i
+
b
3
i
− ^
y
DKS
m
(
i
)
~
x
DKS
m
i
c
1
i
−^
x
DKS
m
(
i
)
~
x
DKS
m
i
c
2
i
,
m
= 1, 2, 3, 4. (7.9.)
У матричној форми систем једначина (8.2.9) може се написати као
y
i
=
B
i
p
i
,
i
= 1, 2, . . . ,
n
e
,
(7.10)
где су:
y
i
=
[
~
y
DKS
1
i
~
x
DKS
1
i
~
y
DKS
2
i
~
x
DKS
2
i
~
y
DKS
3
i
~
x
DKS
3
i
~
y
DKS
4
i
~
x
DKS
4
i
]
,
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
57
B
i
=
[
^
y
DKS
1
(
i
)
^
x
DKS
1
(
i
)
1
0
0
0
− ^
y
DKS
1
(
i
)
~
y
DKS
1
i
− ^
x
DKS
1
(
i
)
~
y
DKS
1
i
0
0
0
^
y
DKS
1
(
i
)
^
x
DKS
1
(
i
)
1
− ^
y
DKS
1
(
i
)
~
x
DKS
1
i
− ^
x
DKS
1
(
i
)
~
x
DKS
1
i
^
y
DKS
2
(
i
)
^
x
DKS
2
(
i
)
1
0
0
0
− ^
y
DKS
2
(
i
)
~
y
DKS
2
i
− ^
x
DKS
2
(
i
)
~
y
DKS
2
i
0
0
0
^
y
DKS
2
(
i
)
^
x
DKS
2
(
i
)
1
− ^
y
DKS
2
(
i
)
~
x
DKS
2
i
− ^
x
DKS
2
(
i
)
~
x
DKS
2
i
^
y
DKS
3
(
i
)
^
x
DKS
3
(
i
)
1
0
0
0
− ^
y
DKS
3
(
i
)
~
y
DKS
3
i
− ^
x
DKS
3
(
i
)
~
y
DKS
3
i
0
0
0
^
y
DKS
3
(
i
)
^
x
DKS
3
(
i
)
1
− ^
y
DKS
3
(
i
)
~
x
DKS
3
i
− ^
x
DKS
3
(
i
)
~
x
DKS
3
i
^
y
DKS
4
(
i
)
^
x
DKS
4
(
i
)
1
0
0
0
− ^
y
DKS
4
(
i
)
~
y
DKS
4
i
− ^
x
DKS
4
(
i
)
~
y
DKS
4
i
0
0
0
^
y
DKS
4
(
i
)
^
x
DKS
4
(
i
)
1
− ^
y
DKS
4
(
i
)
~
x
DKS
4
i
− ^
x
DKS
4
(
i
)
~
x
DKS
4
i
]
,
p
i
=
[
a
1
i
a
2
i
a
3
i
b
1
i
b
2
i
b
3
i
c
1
i
c
2
i
]
,
i =
1, 2, . . . ,
n
e
.
(7.11.)
Према томе, на основу израза (7.10.) могуће је израчунати осам параметара
пројективне трансформације за сваки елеменат
i
. Трансформисане вредности
координата идентичних тачака узорка просторних података могу се онда
израчунати по следећем алгоритму:
1. Примена параметара дводимензионалне трансформације сличности на геодетске
координате идентичних тачака у глобалном геодетском референтном систему
(
X
GRS
,
Y
GRS
) за елеменат у којем је тачка садржана. Као резултат, добијају се
вредности координата идентичних тачака на основу трансформације сличности
(
^
X
DKS
,
^
Y
DKS
);
2. Рачунање вредности координата идентичних тачака у равни Gauss-Krüger
oве
пројекције (
^
y
DKS
,
^
x
DKS
), на основу вредности (
^
X
DKS
,
^
Y
DKS
);
3. Примена параметара пројективне трансформације на координате идентичних
тачака у равни Gauss-Krüger
oве пројекције (
^
y
DKS
,
^
x
DKS
), за елеменат у којем је
тачка садржана, изразима (7.8.). Као резултат, добијају се трансформисане
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
59
обзиром да су једино на целом подручју трансформације вредности (7.13.)
центриране величине.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
60
8. МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА
КРАЉЕВА
На основу скупа геодетских тачака са позицијам одређеним у SRB_ETRS89
референтном систему и Државном координатном систему Републике Србије
неопходно је развити модел грид трансформације за шире подручје града Краљева.
Узорак података представља скуп од 81 тачке премера непокретности за које су
познате координате у оба наведена система. Координате ових тачака одређиване су
применом релативног статичког GPS позиционирања ослонцем на тачке Државне
референтне мреже (SREF) или позиционирањем у односу на Активну геодетску
референтну основу Србије (АГРОС), применом сервиса позиционирање АГРОС
РТК. Имајући у виду начин одређивања ових координата, може се закључити да је
њихова просторна тачност центиметарског нивоа.
Слика 8.1.
Просторни распоред тачака узорка
Карактеристичне вредности за растојање
d
између суседних тачака изабраног
узорка су следеће:
−
максимална
:
d
max
=
9941
m
−
минимална
:
d
min
=
717
m
−
просечна
:
d
sred
=
5329
m
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
62
Слика 8.2.
Вредности резидуала на свим тачкама.
Табела 8.2.
Карактеристичне вредности резидуала после тродимензионалне
трансформације сличности.
Тачка
Northin
g
Easting
Height Тачка
Northing
Easting
Height
101_ZH2
-0.1174m -0.0463m
0.0792m
65_ZH2
0.0185m
0.0582m
0.2343m
104_ZH2
-0.0985m -0.2086m -0.0374m
70_ZH2
-0.1459m
-0.2619
m -0.2052m
105_ZH2
-0.1330m
0.0632m
0.1902m
71_ZH2
0.0765m
-0.1266
m
106_ZH2
-0.0274m
0.0710m
0.2267m
72_ZH2
0.0164m
-0.0453
m
107_ZH2
0.0843m
0.0262m
0.2651m
81_ZH2
0.0355m
0.0559m
0.1807m
108_ZH2
-0.1233m -0.1638m
82_ZH2
0.0481m
0.0299m
0.2526m
109_ZH2
-0.0964m -0.2318m -1.6154m
87_ZH2
0.0823m
0.1273m
0.3370m
10_ZH2
0.1957m
0.0948m
0.3147m
89_ZH2
-0.1276m
0.1322m
0.2709m
113_ZH2
0.0705m
0.1321m -1.4231m
90_ZH2
0.0830m
0.1576m
0.2755m
115_ZH2
-0.1363m
0.4556m -0.2545m
91_ZH2
0.1266m
-0.0016
m
0.2296m
122_ZH2
-0.1543m -0.1973m
0.0667m
93_ZH2
0.0759m
0.0435m
0.2181m
124_ZH2
-0.1407m -0.1044m
96_ZH2
0.0381m
0.0056m
0.1638m
125_ZH2
-0.2735m
0.0027m
97Z_ZH2
-0.0257m
0.0730m
0.1617m
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
63
126_ZH2
-0.1542m -0.1588m
3.3152m
98_ZH2
0.0408m
-0.0340
m
0.1245m
Оцена дисторзија просторних података у тачкама правилног грида извршена је
Поделом подручја трансформације на коначне елементе
(подпоглавље 7.2).
Блокдијаграм процеса оцене вредности дисторзија просторних података у тачкама
правилног грида поделом подручја трансформације на коначне елементе приказан
је на слици 8.3.
Слика 8.3.
Блокдијаграм процеса оцене вредности дисторзија просторних података у
тачкама правилног грида поделом подручја трансформације на коначне елементе.
Подела подручја трансформације на коначне елементе извршена је према следећим
принципима:
- Елементи треба да буду четвороуглови што је могуће правилнијег облика и
приближно једнаке површине;
- Сваки елеменат треба да садржи минимално 4 тачке узорка за оцену параметара
тродимензионалне трансформације сличности;
Подела подручја трансформације на коначне елементе
Рачунање параметара дводимензионалне трансформације сличности
засебно за сваки елемент
Рачунање осредњених вредности трансформисаних координата за
тачке чворове
Примена услова континуитета између суседних елемената
Рачунање трансформисаних координата и вредности дисторзија у
тачкама правилног грида
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
65
Једино у ситуацијама када је тачка чвор учествовала у формирању само једног
елемента (у граничним подручјима) њена позиција је, из практичних разлога и само
у неколико случајева, бирана тако да елеменат обухвати све идентичне тачке узорка
као и тачке за тестирање узорка а да при том елеменат задржи облик што
правилнијег четвороугла.
На овај начин, обезбеђено је да свака тачка чвор учествује у оцењивању параметара
трансформације сличности, за све елементе у чијем формирању учествује, чиме се
умањује ефекат услова континуитета између суседних елемената. Отежавајућа
околност код оваквог приступа је да свака тачка чвор мора да испуни задате
критеријуме конформности у свим елементима у чијем формирању учествује, што
је на подручјима где је узорак просторних података релативно редак понекад било
тешко постићи.
Подручје трансформације је подељено на 42 коначна елемента са следећим општим
карактеристикама:
- максимална површина елемента:
P
max
=
46
k m
2
- минимална површина елемента:
P
min
=
3
k m
2
- просечна површина елемента:
P
sred
=
13
k m
2
- минималан број тачака узорка у оквиру елемента:
n
min
=
1
;
- максималан број тачака узорка у оквиру елемента:
n
max
=
3
;
- просечан број тачака узорка у оквиру елемента:
n
sred
=
1
;
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
66
Слика 8.5.
Подела подручја трансформације на коначне елементе
Релативно велика разлика између максималне и минималне површине елемента као
и разлика у броју тачака у оквиру појединачних елемената резултат су
неопходности прилагођавања поделе у граничним подручјима као и недовољне
хомогености густине узорка.
На тачке у оквиру сваког коначног елемента примењена је дводимензионална
трансформација сличности, подпоглавље 6.3. За сваки елемент позната су два скупа
координата идентичих тачака. Један скуп су координате тачака у Државном
координатном систему – контролне тачке, а други скуп јесу координате добијене
применом тродимензионалне трансформације сличности на целом подручју –
Trimble Total Control.
После израчунавања параметара дводимензионалне трансформације сличности по
елементима, за карактеристичне вредности резидуала узорка и експерименталу
референтну стандардну девијацију, добијене су следеће вредности приказане у
Tабели 8.3.
Табела 8.3.
Основни статистички параметри резидуала по координатним осама и
вектора хоризонталног положаја, након 2D трансформације сличности по
елементима.
Статистика
dY[m
]
dX[m] dP[m]
Минимум
-0.276
-0.239
0.009
Максимум
0.220
0.270
0.321
Средња вредност
0.000
0.000
0.100
Стандардна девијација 0.007
0.007
0.010
Ефекат услова континуитета на тачкама чворовима може се сагледати из одступања
трансформисаних вредности координата тачака чворова по појединачним
елементима од осредњених вредности. Параметри који карактеришу овај ефекат
приказани су у Табели 8.4.
Табела 8.4.
Карактеристичне вредности параметара ефекта услова конинуитета
(пројективна трансформација).
a
1
a
2
a
3
b
1
b
2
b
3
c
1
c
2
0.999
9
-0.0002 2.4011 0.0000
1.000
0
-0.6120 0.0000 0.0000
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
68
- Примена параметара тродимензионалне трансформације сличности за
целокупно подручје трансформације на координате у систему SRB_ETRS89.
- Примена билинеарне инетрполације од четири суседне (најближе тачке)
правилног грида у циљу израчунавања корекција за компоненте позиције и
примена израчунате корекције на вредности трансформисаних координата.
Табела 8.6.
Показатељи перформанси грида оцењеног на основу поделе подручја
трансформације на коначне елементе.
Статистика
dY[m
]
dX[m] dP[m]
Минимум
-0.140
-0.111
0.021
Максимум
0.316
0.440
0.542
Средња вредност
0.013
0.019
0.095
Стандардна девијација 0.007
0.007
0.014
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
69
9. ЗАКЉЧНА РАЗМАТРАЊА
У овом раду разматрана је могућност модела грид трансформације за територију
града Краљева. Основни циљ јесте моделовати дисторзије (изобличења)
просторних података изражених у локалном геодетском референтном систему, које
су последица слабе условљености референтног оквира реализованог терестричким
техникама. За равој модела грид трансформације примењен је поступак поделе
подручја трансформације на коначне елементе. Модел трансформације развијен је
на основу узорка просторних података премера непокретности од укупно 81 тачке
чије су координате познате у систему SRB_ETRS89, оквир ETRF2000 и Државном
координатном систему. На основу примењене тродимензионалне трансформације
сличности на целокупно подручје, затим дводимензионалне трансформације
сличности за сваки коначни елемент и услова континуитета по елементима оцењене
су дисторзије просторних података премера непокретности у тачкама правилног
грида са кораком од 2.5 km.
Може се закључити да је примењеним поступком постигнут висок ниво
сагласности оцена дисторзија просторних података у тачкама правилног грида.
Сагласност оцена дисторзија тачака грида је до на центиметар. Нешто веће разлике
јавиле су се у граничном подручју. На основу резултата тестирања може се
закључити да добијени резултати трансформације могу задовољити потребе
трансформације података премера непокретности у Државни координатни систем.
Међутим развијен модел трансформације тренутно не може да има употребну
вредност из разлога што је од самог усвајања новог референтног система ETRS89 у
широкој употреби трансформациони модел GRIDER2.0. који је законом дефинисан.
Трансформациони модел GRIDER 2.0. јесте модел тарнсфромације за целу
територију Републике Србије и нема довољну тачност за одређена подручја ''
како
пракса каже''.
Модел трансформације поделом подруја на коначне елементе би се могао
применити једино у слуају да се размотри развој хетерогеног грида, односно мањег
интервала грида за урбанизована подручја односно подручја карактерисана
великом густином тачака детаља и нешто ређег на подручјима где је неопходна
нижа тачност трансформације.
МОДЕЛ ГРИД ТРАНСФОРМАЦИЈЕ ЗА ТЕРИТОРИЈУ ГРАДА КРАЉЕВА ПРИМЕНОМ
МЕТОДЕ КОНАЧНИХ ЕЛЕМЕНАТА
,
.
.
Грујичић Ђорђе инж геод
71
IERS Tehnical Note: Conventional Terrestrial Reference System and Frame -
https://www.iers.org/SharedDocs/Publikationen/EN/IERS/Publications/tn/TechnNote32/
tn32_021.pdf?__blob=publicationFile&v=1
(сајту приступљено 10.03.2019)
Републички геодетски завод Р. Србије (2017): Закон о државном премеру и
катастру. Београд.
Републички геодетски завод Р. Србије (2010): Геодетска служба – часопис за
геодезију, картографију и катастар непокретности, Број 112.
Републички геодетски завод Р. Србије (2010): Геодетска служба – часопис за
геодезију, картографију и катастар непокретности, Број 113.
Републички геодетски завод Р. Србије (2011): Геодетска служба – часопис за
геодезију, картографију и катастар непокретности, Број 114.
Републички геодетски завод Р. Србије (2013): Геодетска служба – часопис за
геодезију, картографију и катастар непокретности, Број 116.
