Универзитет у Нишу
Машински факултет
Неуронске мреже
семестрални рад
Моделирање и симулација
Мастер академске студије
Машинске конструкције, развој и инжењеринг
Студент:
Душан Ћирић 14К
Ментор:
Проф. др Бобан Анђелковић
Ниш, Јануар 2017.
Моделирање и симулација
Неуронске мреже
Душан Ћирић 14К
2
Оверио:
Како би неуронска мрежа научила да препознаје и класификује појмове мора
да постоји повратна информација, као кад деца уче тако што им се укаже да је то
што раде добро или лоше. Сви људи користе повратне информације, у сваком
тренутку [1].
Вештачке неуронске мреже уче на исти начин. Обично, кроз процес који се
зове пропагација уназад (енг. Back Propagation). Овај процес подразумева поређење
излаза који мрежа генерише са излазом који је требало да генерише. Разлика
између ових излаза се користи при исправљању тежина веза у мрежи. Најпре се
исправљају тежине ближе излазном слоју, крећући се унатраг, све до улазног слоја.
Пропагација уназад, за неко време омогућава мрежи да учи, редукујући разлику
између стварних и жељених резултата, све док се ове две вредности не поклопе [3].
Када се мрежа истренира са довољном количином података, уводе се нови
подаци, код којих недостаје атрибут по коме се врши класификација, како би се
тестирала њена успешност [1].
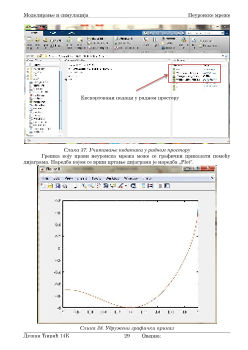
У овом семестралном раду наћи ће се и рачунарски модел за неуронску
мрежу креиран уз помоћ софтвера „MATLAB“. Детаљно ће бити објашњена употреба
овог софтвера на решавање конкретног проблема, одређене математичке функције,
уз помоћ коришћена претрениране неуронске мреже.
Биће предочене могућности и „
моћ
“ једне претрениране неуронске мреже
способне за обављање конкретног задатка.
Моделирање и симулација
Неуронске мреже
Душан Ћирић 14К
3
Оверио:
2.
Неуронске мреже
Неуронска мрежа је један облик имплементације система вештачке
интелигенције, који представља систем који се састоји од одређеног броја међусобно
повезаних процесора или чворова, или процесних елемената које називамо
вештачким неуронима [4].
Неуронске мреже симулирају начин рада људског мозга при обављању датог
задатка или неке функције. Неуронска мрежа је масовно паралелизован
дистрибуирани процесор са природном способношћу меморисања искуственог знања
и обезбеђивања његовог коришћења. Вештачке неуронске мреже подсећају на
људски мозак у два погледа [2]:
Неуронска мрежа захвата знање кроз процес обучавања;
Тежине међунеуронских веза (јачина синаптичких веза) служе за
меморисање знања.
Процедура којом се обавља обучавање је алгоритам обучавања. Кроз овај
поступак се на алгоритамски начин мењају синаптичке тежине у циљу достизања
жељених перформанси мреже. Основну рачунарску снагу неуронских мрежа чини,
паралелност, способност обучавања и генерализација. Генерализација представља
способност продуковања задовољавајућег излаза неуронске мреже и за улазе који
нису били присутни у току обучавања [2].
Тело неурона назива се чвор или јединица. Сваки од неурона има локалну
меморију у којој памти податке које обрађује. Подаци који се обрађују су локални
подаци као и они које се примају преко везе. Подаци који се примају овим каналима
размењују су обично нумерички [4].
Архитектура неуронске мреже представља специфично повезивање неурона у
једну целину. Структура неуронске мреже се разликује по броју слојева. Први слој се
назива улазни, а последњи излазни, док се слојеви између називају скривени
слојеви. Најчешће их има три. Први слој, тј. улазни је једини слој који прима
податке из спољашње средине, следећи (скривени) прослеђује релевантне податке до
трећег (излазиног) слоја. На улазу трећег слоја добијамо коначан резултат.
Сложеније неуронске мреже имају више скривених слојева. Слојеви су међусобно
потпуно повезани [4].
Слојеви комуницирају тако што се излаз сваког неурона из претходног слоја
повезује са улазима свих неурона наредног слоја. Значи, сваки чвор има неколико
улаза и један излаз. Јачина веза којом су неурони повезани назива се тежински
фактор (енг. Weight) [4].
У природи искуство мења стање живог организма тако што он следећи пут
функционише боље у истоветној ситуацији. Вештачке неуронске мреже данас се
користе за научна истраживања као што су пројектовање нових производа и
технологија, процесирање података, моделирање рада система, управљање,
препознавање ликова, планирање и дијагностика итд. У високом степену
представљају поједностављен модел људског мозга, а дефинисане су као група
међусобно повезаних процесуирајућих елемената (неурона) чији је начин рада
сличан стварним људским неуронима. Захваљујући паралелном процесуирању
података, вештачке неуронске мреже су корисне за решавање проблема где не
можемо да пронађемо решење увођењем унапред познатог алгоритма понашања,
али можемо да нађемо доста података – примера (узорака) о природи проблема који
истражујемо [5].
Неуронске мреже се користе у ситуацијама када нису позната правила према
којима би било могуће довести у везу улазне и излазне податке жељеног система [4].
Моделирање и симулација
Неуронске мреже
Душан Ћирић 14К
5
Оверио:
2.2
Модел вештачког неурона
Вештачки неурони, као и биолошки, имају једноставну структуру и имају
сличне функције као и биолошки неурони. Тело неурона се назива чвор или
јединица [6].
Модел неурона чине три базична елемента (
слика 1
)[4]:
Скуп синаптичких тежина
?
??
;
Суматор (линеарни комбајнер) – формира теинску суму улаза;
Активациона функција – лимитира амплитуду излазног сигнала
неурона. Типично се узима нормализација излаза на интервалу
[0, 1]
или
[−1, 1]
.
Вештачки неурон је једноставни елемент процесирања, који извршава
једноставну математичку функцију. Улазне вредности у неурон
?
1
, ?
2
, … , ?
?
, где је
?
укупан број улаза у неурон. Свака улазна вредност се прво множи тежинским
коефицијентом
?
??
, ? = 1,2, … , ?
, где је
?
редни број неурона у неуронској мрежи.
Овако помножене вредности се затим сабирају и добија се вредност
?
?
[6].
?
?
= ∑ ?
??
∙ ?
?
?
?=1
Слика 1.Нелинеарни модел неурона
Ова се вредност користи као улаз у нелинеарну функцију
а
, која зависи од
параметра
?
?
– прага активације. Ова зависност је најчешће таква да се
?
?
одузима
од
?
?
и при томе се њихова разлика користи као улаз у нелинеарну функцију
а
. Тако
да се добија вредност излаза
?
– тог неурона [4, 6]:
?
?
= ? ∙ (?
?
− ?
?
) = ? (∑ ?
??
∙ ?
?
?
?=1
− ?
?
)
Вештачке неуронске мреже имају паралелну дистрибуирану архитектуру са
великим бројем чворова и веза. Свакој вези између два чвора придружен је
тежински коефицијент [6].
