Numeričke serije

Numeričke serije

Numeričke serije su nizovi numeričkih podataka uređenih po hronologiji jer se u obzir uzima
njihov vremenski redosled i ti vremenski periodi moraju biti jednaki.

U ovom radu se analizira proizvodnja i prodaja po kvartalima u tri posmatrane godine pa
momentnih vremenskih serija, jer se momentne odnose na jedan vremenski trenutak.

klasična dekompozicija vremenskih serija polazi od pretpostavke da na promene posmatranih
pojava tokom vremena utiču četiri komponente:



Razvojna tendencija pojave u posmatranom periodu, tj. trend



Ciklična komponenta, kolebanje koje se pojavljuje u određenim, često nejednakim
periodima od više godina



Sezonske varijacije, kolebanje koje se ispoljava u razmacima manjima od jedne
godine i ponavlja se na isti način u dužem nizu godina



Rezidualna komponenta, to su neregularni uticaji koji se pojavljuju kao slučajna
varijacija pojave.

Važno je napomenuti da ne mora svaka vremenska serija da sadrži sve četiri komponente ali
svaka vremenska serija sadrži neregularnu komponentu.

Ovaj rad se prvenstveno bavi vremenskim Sezonskim varijacijama jer smo proizvodnju i
prodaju iskazali po kvartalima, tj. kao kvartalnu seriju.

Kod velikog broja ekonomskih pojava uočavaju se pojedinačne fluktuacije, čije je dejstvo se
ispoljava tokom godinae. godišnji podaci o pojavama ne iskazuju sezonske promene, jer se
one odvijaju u kratćim vremnskim periodima unutar godine. Usled toga sezonske varijacije
mogu se uočiti samo kod vremenskih serija kod kojih su vremneske jedinice kraće od godinu
dana.

Sezonske varijacije predstavljaju promene određenim vremenske serije koje se ponavljaju
tokom više godina u isto doba, u istom smeru i približno istom intezitetu.

Znači da se sezonske varijacije mogu definisati kao stalna tendencija pojave da u pojedinim
periodima godine( mesecima ili kvartalima) varira a odrđen način oko utvrđenog
proseka( mesečnog ili kvartalnog).

Poznato je da npr. cena voća, cena turističkih aranžmana, prodaja piva itd. pokazuje tipične
sezonske oscilacije tokom godine.

Zboga toga se kod osnovnih pojava pažljivo analizira vrsta i stepen sezonskog kolebanja jer je
cilj isključiti dejstva sezonske komponente prilikom projekcije nivoa pojave u narednom
periodu.

Sezonske varijacije mogu biti:



Stabilne-ako se iz godine u godinu menjaju na približno isti način



Nestabilne-akko se posmatrane pojave povećavaju ili smanjuju, radi se o nestabilnim
sezonskim varijacijama

Bez obzira da li je reč o stabilnim ili nestabilnim varijacijama smer i intenzitet sezonskih
varijacija meri se Sezonskim indeksima.

Sezonske varijacije uopštavaju intenzitet sezonkog varijabiliteta za duži vremenski period.

U ovom vremenskom radu razmatraćemo sezonske varijacije sa aspekta multiplikovanog
modela.

Primenom ovog modela, kod sezonskih indeksa, povećana vrednost pojave izražava se sa
100% tako da sezonski indeksi čija je vrednost iznad 100 pokazuju da posmatrana pojava
raste pod uticajem sezone, a indeks čija je vrednost ispod 100 pokazajue da pojava zbog
sezonskih uticaja opada.

Sezonski indeks je relativan broj koji pokazuje prosek sezonskog uticaja, odnosno jačinu
sezonskog uticaja u određenom kvartalu tokom više godina.

U statistici je formulisano više metoda pomoću kojih se sezonske varijacije, kroz sezonske
indekse mogu izolovati tj. izdvojiti od drugih komponenti vremenske serije. U praksi se
uglavnom koristi metod odnosa originalnih podataka prema pokretnim prosecima odnosno
pokretnim sredinama i on je primenjen u ovom radu.

Pokretni procesi su takva transformacija originalne vremenske serije u kojoj se svaki podatak
zamenjuje aritmetičkom sredinom tog podatka, određenog broja predhotnih i isto toliko
narednih podataka.

Pokretni procesi su dobili naziv po tome jer sukcesivno izračunavamo proseke i pomeramo se
od početka serije sve do njenog kraja. Pri tome, stvarno uzimamo grupe od istog broja
podataka za izračunavanje proseka.

Metod odnosa prema pokretnim procesima polazi od multiplikovanog modela kompozije
vremenske serije: Y=T*S*C*R, a u ovom modelu su:

T-trend

C-ciklična kolebanja

S-sezonske varijacije

R-Rezidualna komponenta

Očigledno je da iz ovog modela kompozicije vremenske serije treba eliminisati trend, cikličnu
i neregularnu komponentu kako bi u njoj ostao samo čist uticaj sezone.

Kada bismo imali tri indikatora koji bi odražavali poseban uticaj svake od tri komponente
tada bismo podelili originalne podatke sa sva tri indikatora i došli bi do mere sezonskih
uticaja: S=Y/(T*C*R)

Problem je što neregularnu komponentu nije moguće obuhvatiti preko nekog posebnog
pokazatelja jer je to slučajna promenjljiva. Sličan problem je i sa cikličnom komponentom.

Ideja metoda odnosa prema pokretnim sredinama o tome kako odstraniti T,C i R iz vremenske
serije je u sledećem:

Trend i ciklična komponenta (T i C) se ne obuhvataju pojedinačno, već združeno kroz
odgovarajuće kvartalnne, pokretne proseke.

O preduzeću

To je najveća ciglarska kompanija u Jugoistočnoj Evropi. Firmu je osnovao 1866. godine
Mihael Bohn rodonačelnik ciglarstva, creparstva na ovim prostorima, zbog čega Kikinda slovi
kao prestonica crepa i keramike, odnosno centar srpske industrije opeke.

Razvila je sopstveni brend sa kvarcnim pokrivačem, crepom kao najpoznatijom robnom
markom još od 1900. godine. Pored toga od 1972. godine proizvodi keraičke pločice.

Proizvodni program kompanije podeljen je na dve osnovne grupe:

a) Fina keramika- ova grupa obuhvata podne pločice, zidne pločice i dekorativnu

keramiku

b) Gruba keramika- obuhvata crep blokovsku robu i upotrebu keramike

Glavni pojedinačni proizvod je crep, pre svega zbog iskustva u proizvodnji ovog neizostavnog
zaštitnog dela kuće jer se to iskustvo ogleda u vremenskom periodu dužem od jednog veka.

Industrijski kompleks „Toza Marković“ Kikinda se prostire na 214 hekatra a proizvodni
kapaciteti su:

100 miliona komada crepa

2 miliona kvadratnim metara zidnih

1 miliona kvadratnih metara podnih pločica

13500 tona keramičih Frita i glazura

U fabrici „Toza Marković“ izvršena je neuspešna privatizacija i preduzeće je dospelo u stečaj.

Stečajni postupak trajao je oko dve i po godine i zaključen je polovinom Avgusta 2016.
godine, nakon usvajanja plana reorganizacije. po tom planu potraživanja poverilaca
pretvorena su u vlasnički udeo pa je većinski vlasnik postalo javno preduzeće „Srbija Gas“ sa
vlasničkim udelom oko 66%.

U fabrici je zaposleno oko 600 radnika ali je najveći deo njih zaposlen na određeno vreme,
prvenstveno zbog toga što je stečajni postupak takve pravne procedure koja predviđa otkaz za
sve zaposlene.

Studija slučaj- analiza sezonskih varijacija proizvodnje i prodaje Grube
keramike i fine keramike kod preduzeća „Toza Marković“ Kikinda u
periodu 2011-2013. godine

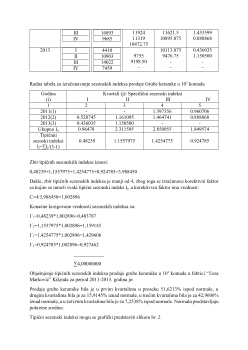
I.Radna tabela za izračunavanje specifičnih sezonskih indeksa proizvodnje grube keramike u
fabrici “Toza Marković“ Kikinda

Godina

Kvartal

Proizvodnja

grube

Pokretne

sredine

Centrirane

pokretne

Specifični

sezonski

(i)

(j)

keramike u

komada
(Y

)

(Ȳ

)

sredine

(Ȳ'

)

indeksi

)

2011

(1)

III

8819

12002
17025
12392

12559.50
11597.75
12306.05

12078.625
11952.125

12165.25

1.409515
1.036803
0.408705

2012

(2)

III

4972

14837
15895

8122

12024

10956.50

10747

9885.50

11490.25
10851.75
10316.25

1.291269
1.464741
0.787302

2013

III

4134

11391
15278

7340

9731.25
9528.25

9808.375

9625.75

0.421477
1.182897

Radna tabela za izračunavanje sezonskih indeksa proizvodnje Grube keramke u 10

dinara

Godina

(i)

Kvartali (j)/ Specifični sezonski indeksi

I II III IV

2011(1)

1.409515

1.036803

2012(2)

0.408705

1.291269

1.464741

0.787302

2013(3)

0.421477

1.182897

Ukupno I

0.830182

2.474166

2.874256

1.824165

Tipičnni sezoski

indeksi

=∑I

/(3-1)

0.415091

1.237083

1.437128

0.9120525

Zbir tipičnih sezonskih indeksa iznosi:

0.415091+1.237083+1.437128+0.9120525=4.001355

Dakle, zbir tipičnih sezonskih indeksa je više od četiri, zbog čega se izračunava korektivni
faktor sa kojim se množi svaki tipični seonski indeks Ij I korektivni faktor ima vrednost:

C=4/4.001355=0.999661

Konačne korigovane vrednosti sezonskih indeksa su:

I´

=0.415091*1.999661=0.414950

I´

=1.237083*0.999661=1.236664

I´

=1.437128*0.999661=1.436642

I´

=0.9120525*0.999661=0.911744