Medicinski fakultet Niš,
integrisane akademske studije stomatologije
Seminarski rad iz medicinske statitstike i informatike
PARAMETRIJSKI TESTOVI U
BIOSTATISTICI
Student:
Niš, 2015
SADRŽAJ:
1. Testiranje hipoteze
2. Statistička i biološka (klinička) značajnost
3. Studentov t-test
3.1.
Ocena značajnosti razlike aritmetičkih sredina dva nezavisna uzorka
3.2.
Ocena značajnosti razlike proporcija dva uzorka
4. Analiza varijanse
5. Z-test
6. Primer za studentov t test
7. Zaključak
Literatura
Postavlja se (najčešće) u svrhu odbacivanja. Odbacuje se ili prihvata.Na primer,ako
ispitujemo da li postoji razlika u visini holesterola u krvi između gradskog I seoskog
stanovništva,onda nulta hipoteza glasi: između holesterola u krvi gradskog I seoskog
stanovništva ne postoji statistički značajna razlika.
Alternativna hipoteza, H1 (engl. alternative hypothesis) vredi ako nulta hipoteza nije istinita.
Najčešće se direktno odnosi na teorijsku pretpostavku koja se želi istražiti, tj. često je
alternativna hipoteza upravo hipoteza istraživača.U prostom obliku,ona glasi “ima
razlike”između pojava koje ispitujemo i merimo i ta razlika je statistički značajna.
Statistički test računa tzv. p-vrednost. To je verovatnost dobijanja uočene ili još veće razlike
na slučajnim uzorcima iste veličine iz populacija koje se u istraživanom obeležju ne razlikuju,
tj. pod pretpostavkom da je nulta hipoteza tačna. Što je p-vrednost manja, to je manje
verovatno da je nulta hipoteza tačna, dok velika p-vrednost sugerira prihvatljivost nulte
hipoteze. Iako verovatnost tačnosti nulte hipoteze odgovara p-vrednosti, njenu tačnu vrednost
ne znamo. Nemoguće je, naime, izračunati verovatnost neke pretpostavke polazeći od toga da
je ona tačna. Ipak, iz p-vrednosti moguće je izračunati, koristeći tzv. Bayesovu statistiku, za
koliko istraživanje na našem uzorku modificira dotadašnju procenu verovatnosti nulte
hipoteze.
1 - p = odgovara verovatnosti da nulta hipoteza nije tačna, tj. da stvarna razlika postoji I
naziva se nivo značajnosti. Što je p-vrednost manja, nivo značajnosti je veći, tj. pouzdanija je
procena stvarnih iz uočenih razlika.
Ponekad unapred znamo da neko obeležje populacije A ne može biti prosečno manje nego u
populaciji B, a nismo sigurni da li je veće (ili obrnuto).
Npr. ispitujemo novi lek za sniženje krvnog pritiska. Poznato je da taj lek ne može povisiti
krvni pritisak, ali nije poznato da li ga smanjuje i koliko.
Ta testiranja se zovu jednosmerni testovi (one-tailed), nasuprot standardnim, dvosmernim
testovima (two-tailed). Kod jednosmernih testiranja iste opažene razlike daju duplo manje p-
vrednosti (nivo značajnosti je veći!), jer je 50% slučajnih ishoda unapred isključeno.
Jednosmerna testiranja treba kritički koristiti. U praksi su retka. Ako se posebno ne istakne
suprotno, test je dvosmerni.
Često na osnovu rezultata statističkih testova donosimo odluke (npr. proizvodnja novog leka,
primena nove metode lečenja, dijagnosticiranje bolesti i sl.). To nas ponekad prisiljava da
definišemo: granicu nivoa značajnosti (1- graničnu p-vrednost).
Graničan je onaj nivo značajnosti iznad koje prihvatamo da su uočene razlike stvarne, tj.
zanemarujemo malu verovatnost (p-vrednost) da se radi o slučaju.
Kažemo da se uzorci statistički značajno razlikuju ako je dobijena p-vrednost testa manja
od granične p-vrednosti.
Ako to nije slučaj, tj. ako je p-vrednost testa veća ili jednaka od granične p-vrednosti,
kažemo da se uzorci ne razlikuju statistički značajno.U prvom slučaju nultu hipotezu
odbacujemo, a u drugom je prihvatamo.
U biomedicini je uobičajena 95% granični nivo značajnosti, odnosno čuvena granična p
vrednost= 5%.
Tu graničnu p-vrednost valja uzeti sa “debelom” rezervom. Ako npr. u poređenju novog leka
sa starim dobijemo p=0.049, novi lek prihvatamo, dok ga u slučaju p=0.051 ne prihvatamo.
Razlika je drastična, a verovatnosti da novi lek nema prednosti pred starim su podjednako
male u oba slučaja (4.9 i 5.1%).No, tako je uvek kada moramo odrediti granice (student koji
na testu ima jedan bod ispod praga prolaznosti verovatno se ne razlikuje od onoga koji je
prošao s jednim bodom više).
Razgraničenje pomoću graničnog nivoa značajnosti povlači mogućnost grešaka u
zaključivanju.
Alfa greška (ili greška tipa 1) je odbacivanje nulte hipoteze, dok je ona u stvari tačna.
Dakle, na osnovu rezultata statističkog testa utvrdili smo da postoji razlika u
istraživanom obeležju između populacija, iako ta razlika ne postoji, tj. na našim
uzorcima smo je dobili slučajno. Verovatnost alfa greške odgovara p-vrednosti.
Verovatnost da nećemo napraviti grešku tipa 1 odgovara nivou značajnosti (1-p).
Beta greška (ili greška tipa 2) je prihvatanje nulte hipoteze, dok je ona u stvarnosti
netačna. Drugim rečima, razlika nađena na uzorcima nije testom bila statistički
značajna, iako se populacije u istraživanom obeležju razlikuju. Verovatnost beta
greške zavisi od toga šta prihvatamo kao stvarnu razliku u posmatranoj veličini.
Drugim rečima moramo definisati šta smatramo stvarno značajnom razlikom (u
medicini govorimo o biološkoj ili kliničkoj značajnosti). Jasno je da ćemo vrlo male
razlike teže statistički potvrditi nego relativno velike.
Verovatnost da nećemo napraviti grešku tipa 2 povezana je sa snagom istraživanja.Snaga
istraživanja raste s veličinom uzorka (N) i s veličinom razlike koju smatramo stvarno
značajnom, a opada sa nivoom značajnosti (statističke). Ako nismo prisiljeni određivati
granice, dobijene p-vrednosti prosuđujemo zavisno od toga da li smo uočene razlike očekivali
(npr. nećemo odbaciti p=0.08 u poređenju visina desetogodišnjih dečaka i devojčica, jer je to
fiziološki očekivani rezultat), ili su neočekivani rezultat u mnoštvu poređenja (ako se kocka
često baca, pojaviće se i malo verovatne kombinacije, poput tri šestice zaredom).
Nadalje su važne i posledice interpretacije testa. Tako ćemo teško prihvatiti novi lek i pored
toga što je gotovo sigurno delotvoran (npr. p=0.01), ako je njegova proizvodnja vrlo skupa (u
praksi se radi o milijardama dolara), dok ćemo manje oklevati u slučaju leka koji može spasiti
život, a ne postoji slični.Zbog toga se u novije vreme sve češce rezultati statističkih testiranja
dopunjuju iskazima koji sadrže više informacija od same činjenice da li je dobijena p-
vrednost testa veća ili manja od izabrane granične p-vrednosti. Radi se o tzv.:
intervalima pouzdanosti (C.I., prema engl. Confidence Interval)
Naime, na temelju uočenih razlika između uzoraka, mogu se, sa zadanom pouzdanošcu,
proceniti intervali mogućih vrednosti stvarnih (populacijskih) razlika. Tako je najcešce u
upotrebi tzv. 95% interval pouzdanosti (95 % C.I.).
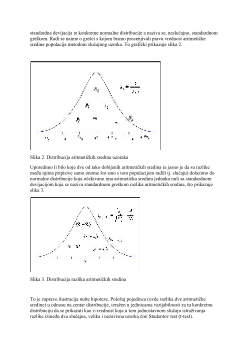
standardna devijacija te konkretne normalne distribucije a naziva se, neslučajno, standardnom
greškom. Radi se naime o grešci s kojom bismo procenjivali pravu vrednost aritmetičke
sredine populacije metodom slučajnog uzorka. To grafički prikazuje slika 2.
Slika 2. Distribucija aritmetičkih sredina uzoraka
Uporedimo li bilo koje dve od tako dobijenih aritmetičkih sredina (a jasno je da su razlike
među njima pripisive samo onome što smo s tom populacijom radili tj. slučaju) dolazimo do
normalne distribucije koja očekivano ima aritmetičku sredinu jednaku nuli sa standardnom
devijacijom koja se naziva standardnom greškom razlika aritmetičkih sredina, što prikazuje
slika 3.
Slika 3. Distribucija razlika aritmetičkih sredina
To je zapravo ilustracija nulte hipoteze. Položaj pojedinca (ovde razlika dve aritmetičke
sredine) u odnosu na centar distribucije, izražen u jedinicama varijabilnosti za tu konkretnu
distribuciju da se prikazati kao z-vrednost koja u tom jednostavnom slučaju istraživanja
razlike između dva slučajna, velika i nezavisna uzorka čini Studentov test (t-test).
