VISOKA TEHNIČKA ŠKOLA STUKOVNIH STUDIJA
NIŠ
PRIMENA LINEARNOG
PROGRAMIRANJA U
GRAĐEVINARSTVU
Profesor Student
Dr Milorad Zlatanović
1
UVOD
Operaciona istraživanja predstavljaju skup modela, kvantitativnih metoda i algoritama,
pomoću kojih se određuje najpovoljnije rešenje složenih problema iz svih oblasti delovanja ljudi.
Naziv potiče od istraživanja operacija u organizacionim sistemima sa ciljem njihove
optimizacije. Operaciona istraživanja su se najpre razvila u vojne svrhe, da bi kasnije bila uočena
njihova upotrebljivost u upravljanju poslovnim sistemima.
Osnovni zadaci operacionih istraživanja, kao primenjene i eksperimentalne nauke, su opis
ponašanja sistema ili procesa, analiza (simulacija) ponašanja sistema ili procesa u izmenjenim
uslovima i predviđanje tog ponašanja u budućnosti. U procesima opisa, analize i predviđanja
teorije operacionih istraživanja koriste se mnogobrojne matematičke discipline kao što su:
matematička analiza, teorija verovatnoće, teorija igara, statistička teorija, matematička logika,
linearno, nelinearno i dinamičko programiranje, teorija masovnog opsluživanja, heurističko-
matematičko programiranje i druge.
Osnovna karakteristika operacionih istraživanja je razvijanje matematičkog modela
sistema ili procesa koji se posmatra, na osnovu kojeg će biti moguće predviđanje i upoređivanje
posledica različitih varijanti u procesu odlučivanja. U skladu s tim, suština metoda operacionih
istraživanja jeste nastojanje da se vrednost postavljenog cilja optimizuje i time na racionalnoj
osnovi pripremi konačna odluka. Iako na ciljeve svakog poslovnog sistema deluje veliki broj
uticajnih faktora, svi oni se mogu podeliti u dve grupe:
podaci - kao prirodne ili institucionalno date veličine, koje se mere ili opažaju i na koje se ne
može uticati
parametri odluke - kao veličine koje se mogu svesno menjati unutar datih granica (same
granice su veličine koje pripadaju klasi podataka i ne mogu se menjati).
I dok su podaci i parametri odluke veličine međusobno povezane sistemom funkcija
ograničenja, koje utiču na optimalnu vrednost postavljenog cilja, veličine cilja i relevantnih
faktora međusobno su povezane funkcijom cilja. Optimalno rešenje predstavlja ona kombinacija
uslova koja daje željenu ekstremnu vrednost funkcije cilja, prema usvojenom kriterijumu
optimizacije (minimumu – ako funkcija cilja predstavlja neki vid troškova, odnosno maksimumu
– ako funkcija cilja predstavlja neki vid dobiti).
3
Uslovi potrebni da se linearno programiranje može primeni u rešavanju
konkretnih zadataka:
1.
Potrebna je jasna formulacija cilja koji se u datim uslovima može realno zahtevati, mada u
praksi nije uvek lako naći jedinstveni kriterijum koji dozvoljava da se bezuslovno odbaci jedan, a
usvoji drugi program. Međutim, taj jedinstveni kriterijum se mora naći.
2.
Specifični uslovi - ograničenja su zasnovana na postojećim izvorima, planskim proporcijama i
drugim faktorima koji određuju dozvoljena rešenja. Pošto je u praksi teško uzeti u obzir sve
postojeće faktore, potrebno je, kao i pri izboru kriterijuma optimalnosti, eksperimentisanje i
iskustvo da tako postavljeni model, u poređenju sa stvarnošću, ne izgubi realni karakter i
praktičnu vrednost.
3.
Zadatak treba da dozvoli dobijanje niza rešenja koja daju različite programe, da bi se izabrao
onaj koji je optimalan za date uslove.
4.
Model zadatka linearnog programiranja treba da sadrži linearne jednačine, tj. da realne
zavisnosti ne protivureče ovom zahtevu.
2. OPŠTI PROBLEM LINEARNOG PROGRAMIRANJA
Problem linearnog programiranja pripada problemima matematičkog programiranja koji
se sastoje u traženju minimalne ili maksimalne vrednosti funkcije na nekom određenom skupu.
Problem minimizacije (maksimizacije) može se zapisati u obliku:
?
(
?
) →
???
(
???
)
?
∈
?
gde je funkcija cilja
?
(
?
) definisana na skupu
?
. Posmatra se skup
?
koji je podskup realnog
?
-
dimenzionalnog prostora
?
∈
ℝ
. Svaki vektor
?
∈
?
se naziva dopustivo rešenje problema, a
skup
?
se naziva dopustiv skup. Vektor
?
∗
∈
?
za koji funkcija cilja dostiže svoj minimum ili
maksimum naziva se optimalno rešenje. Ako je funkcija cilja (
?
) linearna i ako je skup
?
definisan linearnim ograničenjima, onda je reč o problemu linearnog programiranja. U ostalim
slučajevima reč je o nelinearnom programiranju.
4
Od sad nadalje posmatraćemo problem minimizacije. Problem maksimizacije se može
svesti na problem minimizacije množenjem funkcije cilja sa (−1).
Najčešći oblici problema linearnog programiranja su:
1.
Opšti oblik
?
(
?
) =
⟨
?
,
?⟩
→
???
,
?
,
?
∈
ℝ
?
?
∈
?
= {
?
∈
ℝ
,
??
≤
?
,
?
’
?
=
?
’,
?
≥ 0,
?
∈
ℝ
?
,
?
,
?
∈
ℝ
?
,
?
’
∈
ℝ
?
,
?
,
?
’
∈
ℝ
?
} (1)
2.
Standardni oblik
?
(
?
) =
⟨
?
,
?⟩
→
???
,
?
,
?
∈
ℝ
?
?
∈
?
= {
∈
ℝ
?
,
??
≤
?
,
?
≥ 0,
?
∈
ℝ
?
,
?
,
?
∈
ℝ
?
} (2)
3.
Kanonički oblik
?
(
?
) =
⟨
?
,
?⟩
→
???
,
?
,
?
∈
ℝ
?
?
∈
?
= {
∈
ℝ
?
,
??
=
?
,
?
≥ 0,
?
∈
ℝ
?
,
?
,
?
∈
ℝ
?
} (3)
pri čemu je
?
= (
?
1
, … ,
?
?
)
?
,
?
= (
?
1
, … ,
?
?
)
?
,
?
??
su elementi matrice
?
,
?
??
′
su elementi matrice
?
′ ,
?
= (
?
1
, … ,
?
?
)
?
,
?
′ = (
?
1 ′
, … ,
?
?
′
)
?
.
Teorema 1.1.1. (o rešivosti problema linearnog programiranja)
Problem linearnog programiranja nema rešenje ako je dopustiv skup prazan ili ako
funkcija cilja nije ograničena sa donje strane, u protivnom problem linearnog programiranja ima
rešenje i to rešenje je ili jedinstveno ili ih ima beskonačno mnogo.
Definicija 1.1.1
.
Dat je problem (
?
) =
⟨
?
,
?⟩
→
???
,
?
∈
?
= {
∈
ℝ
?
,
?
≥ 0,
??
=
?
}, gde je
?
≠ 0,
?
∈
ℝ
?
,
?
,
????
(
?
) =
?
=
?
,
?
∈
ℝ
?
.
?
je bazično rešenje problema ako postoji
?
linearno nezavisnih
vektora kolona matrice
?
, (
?
?
1
,
?
?
2
, … ,
?
??
) tako da važi
?
?
1
?
?
1
+
?
?
2
?
?
2
+
⋯
+
?
??
?
??
=
?
.
6
optimalno rešenje problema, a ako je ∆
?
≤ 0 za
?
=
?
+ 1, … ,
?
i postoji neko
?
∈
{
?
+ 1, … ,
?
}
tako da je ∆
?
= 0, tada problem (3) ima beskonačno mnogo rešenja. Ako postoji
?
∈
{
?
+ 1, … ,
?
} tako da je ∆
?
> 0 tada
?
nije optimalno rešenje problema (3). Ako postoji
?
∈
{
?
+ 1, … ,
?
}
tako da je ∆
?
> 0, a
?
??
≤ 0 za
?
= 1, … ,
?
, tada problem (3) nema rešenja jer funkcija cilja nije
ograničena sa donje strane, tj.
?
(
?
) → −∞.
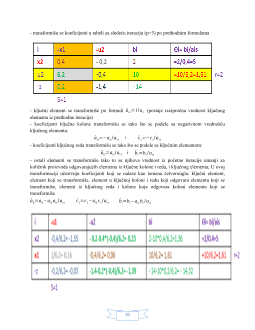
3. SIMPLEKS METODA
George Dantzig je 1947. godine razvio efikasan metod, simpleks algoritam za rešavanje
problema linearnog programiranja. Ovaj algoritam je korišćen za rešavanje problema u različitim
industrijskim granama kao što su bankarstvo, obrazovanje, šumarstvo, naftna industrija,
transport, itd.
Simpleks metoda je opšta metoda za rešavanje problema linearnog programiranja.
Simpleks metoda spada u iterativne metode. Ona polazi od nekog dopustivog rešenja pa ga u
nizu koraka poboljšava sve dok ne dođe do najboljeg, tj. optimalnog rešenja. Simpleks metoda je
konačna iterativna metoda jer se u konačnom broju iteracija dolazi do optimalnog rešenja. Ovde
će biti navedena simpleks metoda za probleme bez degeneracije.
Algoritam koji pretpostavlja poznavanje jednog vrha (ekstremne tačke, bazičnog rešenja),
zove se sekundarni algoritam, a algoritam koji nalazi početni vrh za sekundarni algoritam ili
konstatuje da je skup ograničenja prazan, tj. da problem nema rešenja naziva se primarni
algoritam.
Neka je dat problem linearnog programiranja bez degeneracije oblika
?
(
?
) =
⟨?
,
?⟩
→
???
,
?
,
?
∈
ℝ
?
?
∈
?
= {
?
∈
ℝ
,
??
=
?
,
?
≥ 0},
?
> 0, (4)
gde je
?
= (
?
1
, … ,
?
?
)
?
, a
