
Proizvodna funkcija Pregled
VISOKA POSLOVNAA ŠKOLA
STRUKOVNIH STUDIJA
NOVI SAD
SEMINARSKI RAD
PROIZVODNA FUNKCIJA
Student:
Marija Milić
Novi Sad, decembar, 2013.
SADRŽAJ
SADRŽAJ
................................................................................................................. 3
1. UVOD
........................................................................................................................
5
2. OPTIMALNA INTENZIVNOST PROIZVODNJE
.............................................
5
2.1 Osnove
.................................................................................................................
5
2.2 Analiza proizvodne funkcije jednog faktora
...................................................
8
2.3 Analiza proizvodne funkcije s menjanjem nivoa u efikasnosti
....................
13
2.4 Analiza proizvodne funkcije s više faktora
....................................................
15
2.5 Funkcija troškova
............................................................................................
16
2.6 Analiza osetljivosti s funkcijom troškova
......................................................
18
3. ODNOS FAKTOR - FAKTOR
.............................................................................
19
3.1 Kombinacija s minimalnim troškovima
.........................................................
21
3.2 Rast
....................................................................................................................
23
4. ODNOS PROIZVOD - PROIZVOD
....................................................................
24
5. OPTIMALNA ORGANIZACIJA
........................................................................
28
6. ZAKLJU
Č
NA RAZMATRANJA
.........................................................................
28
3

1. UVOD
Neoklasična teorija je univerzalna i sveobuhvatna teorija ekonomike proizvodnje.
Ona definiše ravnotežu i temelji se na sledećim pretpostavkama:
-
savršena predvidivost
-
maksimalna dobit u nekom razdoblju je cilj ekonomske aktivnosti
-
statički pristup proizvodnom procesu
-
neograničena deljivost sredstava za proizvodnju i proizvoda.
1.
Savršena predvidivost – predpostavlja da je rezultat ekonomske aktivnosti
unapred poznat. U poljoprivredi ta je ta pretpostavka neprovediva, jer
pretpostavlja da je prinos nekog usjeva nepristrana funkcija aktivnosti koje je
farmer poduzeo (ili propustio poduzeti),
2.
Maksimizacija dobiti u određenom razdoblju – podrazumeva da posledice odluka
u tekućem periodu neće biti razmatrane u bilo kojem budućem periodu. Izlaz iz
moguće nedoumice može biti u produženju razmatranog perioda na nekoliko
godina i/ili u uvođenju uslova da proizvodne prilike budu iste i nakon
razmatranog razdoblja.
3.
Statički pristup proizvodnom procesu – je skoro isti kao i prethodna pretpostavka,
ali nudi rešenje prethodne nedoumice.
Stati
č
ki
znači da odluke u razmatranom
razdoblju neće uticati na odluke u drugim razdobljima.
4.
Neograničena djeljivost sredstava za proizvodnju i proizvoda – znači da kad god
se sredstvo koristi u proizvodnji ili kad god se proizvedu proizvodi, dostupni su u
bilo kojem svom delu. Ovo je pojednostavljenje kalkulacije troškova.
Naravno, niti jedna od navedenih pretpostavki, se u stvarnosti ne može naći. No
neoklasi
č
na
teorija proizvodnje
je usprkos ovim nedostacima široko prihvaćena.
Zašto?
To je jedina celovita teorija proizvodnje i kad god se jedna od pretpostavki pokaže
ograničavajuća, teorija može biti proširena i proširuje se.
Maksimalni profit u određenom periodu je postignut kad su sva tri od slijedećih
uslova ravnoteže ispunjena:
-
optimalni pojedinačni intenzitet ili optimum količine inputa, tj. optimalan odnos
input-proizvod (eng.
factor-product relationship
)
-
optimalna kombinacija inputa, tj. optimalan odnos input-input (eng.
factor-
factor
relatinoship
)
-
optimalna proizvodna kombinacija (naziva se i optimalna kombinacija
proizvoda), tj. optimalan odnos proizvod-proizvod. (eng.
product-product
relationship
)
2. OPTIMALNI POJEDINA
Č
NI INTENZITET (OPTIMUM KOLI
Č
INE
INPUTA)
2.1 Osnove
Kod proizvodnje se očekuje da će s porastom ulaganja proizvodnih faktora rasti i
količina proizvoda. No, već je Turgot (1727.-1781.), u svom
input-output zakonu
,
uvidio da količina proizvoda raste sporije od stope porasta količine inputa. Ovu
pojavu nazivamo
zakon
opadaju
ć
ih prinosa
jer količina proizvoda jedne jedinice
inputa biva sve manja s povećanjem
ukupne količine proizvodnje. Odnos inputa i
outputa se naziva
proizvodna funkcija
. Proizvodna funkcija uvek opisuje
fizi
č
ki
(koli
č
inski)
odnos između inputa (ili faktora) kao nezavisne varijable i outputa (ili
učinka) kao zavisne varijable. Osim proizvodne funkcije s opadajućom stopom
povrata, postoje i drugi odnosi. Tako razlikujemo slijedeće odnose faktor-učinak
(slika 1.1.)
5
-
proporcionalni odnos, linearni, s konstantnom stopom povrata,
-
ispod proporcionalni odnos, degresivni, s opadajućom stopom povrata,
-
iznad proporcionalni odnos, progresivni, s rastućom stopom povrata,
-
u početku degresivni, a zatim proporcionalni odnos, Neoklasični model, s
promenljivom stopom
-
proporcionalni odnos s pravcem kapaciteta, linearni ograničeni, konstantna stopa
Slika 2.1. Najčešći oblici funkcije proizvodnje (odnosa faktor-učinak)
Iznad proporcionalni rast prinosa, kao posljedica porasta inputa je jako rijedak, iako
je moguć kod inputa pesticida ili rada. Ovakav tip odnosa vrijedi samo u odre enom
rasponu utroška, a nakon toga se mijenja u ispod proporcion alni oblik, što nas
dovodi do
neoklasi
č
ne
proizvodne funkcije
.
Slučaj s proporcionalnim rastom je prilično rijedak: npr. količina mlijeka kao
funkcija hranidbe koncentratom. Ovdje se tako er, može o čekivati da svako daljnje
dodavanje inputa od odre ene razine neće povećavati količinu mlijeka, pa imamo
slučaj linearnog ograničenja proizvodne funkcije.
Najčeš ći slučaj je proizvodna funkcija s ispod proporcionalnim rastom outputa. I u
poljoprivredi je smanjivanje prinosa nakon odre ene količine inputa uobičajeno.
Neoklasična proizvodna funkcija je idealiziran oblik proizvodne funkcije. Ona sadrži
iznad proporcionalne, skoro proporcionalne i ispod proporcionalne faze, te faze s
negativnim povratima.
6
jer npr. farmer obično može mijenjati ne jedan već i više inputa, zbog čega su od
interesa u razmatranju.
Zbog jednostavnosti, neko ćemo se vrieme držati jednodimenzionalnih slučajeva.
Označiti ćemo input slovom
x
, i proizvod slovom
y
. Za input x koristićemo i izraz
faktor, a za proizvod y koristimo i izraze
u
č
inak
i
output
.
2.2 Analiza proizvodne funkcije jednog inputa
Podsetimo se da je jedan od uslova optimuma u neoklasičnoj teoriji proizvodnje,
optimalan odnos input-proizvod. Taj se optimalni odnos može naći pomoću analize
proizvodne funkcije. Za analizu proizvodne funkcije moramo poznavati neke
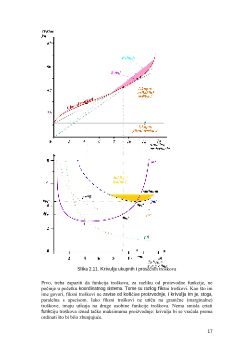
pojmove i definicije koje možemo promotriti na slici 2.4. Prvo što vidimo je
postojanje određenog maksimalnog prinosa. To je najveći prinos koji se može dobiti
utroškom promatranog inputa bez menjanja ostalih faktora
1
.
Tačka maksimalnog prinosa uvijek mora postojati: u nekim slučajevima se
proizvodna funkcija približava maksimumu asimptotski, dok u drugima, kao na slici,
funkcija opada nakon što dostigne maksimum.Treba biti jasno da je svako ulaganje
iznad maksimuma neekonomično.
U nekoliko smo navrata koristili pojam
stopa povrata
i rekli smo da ona može rasti
ili padati. Kada stopa povrata raste ili opada znači da nije konstanta, da se menja.
Dakle, u svakoj tački proizvodne funkcije stopa povrata je drugačija. U razmatranju
određene tačke na proizvodnoj funkciji zanima nas stopa povrata u toj tački, drugim
rečima na granici (margini) našeg razmatranja. Stoga ćemo ovu stopu nazivati
marginalna (grani
č
na) stopa
povrata (MSP
).
MSP definiramo kao promenu učinka
izazvanu zadnjom jediničnom
promenom inputa.
MSP je nagib proizvodne funkcije u tački od interesa. Geometrijski ona se definše
kao nagib tangente povučene na krivulju funkcije proizvodnje u tački koju
razmatramo, a matematički je to prva derivacija funkcije proizvodnje u toj tački.
Može se izračunati kao koeficent promene outputa i promenu inputa, odnosno
y/
x,
a ako su promene
x
jako male, možemo koristiti kontinuiranu jednačinu
dy/dx
. U
donjem delu slike 2.4. MSP je prikazana kao kontinuirana funkcija krivom "granični
proizvod". Ona ima maksimum tačno u tački infleksije proizvodne funkcije.
Funkcija
magrinalne stope povrata je prva derivacija
proizvodne funkcije i govori nam koliki
se u
č
inak može o
č
ekivati od pove
ć
anja inputa za jednu jedinicu (pri određenom
nivou outputa).
Druga informacija koju možemo dobiti iz proizvodne funkcije je prosečni proizvod,
odnosno prosečan učinak po jedinici inputa. Matematički je to odnos
y/x
. U donjem
dijelu slike 2.4. je ovaj odnos takođe prikazan kao kontinuirana funkcija
prose
č
nog
proizvoda.
Geometrijski je prosečan prinos izražen kao nagib pravca povučenog od
cilja kroz posmatranu tačku na proizvodnoj funkciji. Maksimalni prosečni proizvod
je u tački gde taj pravac ima najmanji nagib. Još je jedna tačka zanimljiva: kriva
prosečnog proizvoda preseca krivu marginalne stope povrata (graničnog proizvoda) u
trenutku kad dostigne maksimum.
Razmotrimo sad mogućnosti određenja najviše i najniže koli čine inputa koju
možemo uzeti u razmatranje za ekonomski prihvatljivu proizvodnju. Već smo prije
rekli koja je maksimalna količina inputa što je možemo uzeti u razmatranje. Iz ra
sprave o prosečnom proizvodu i marginalnoj stopi povrata, možemo odrediti
minimaln u količinu koju treba uzeti u razmatranje: to je količina inputa pri kojoj
prosečni proizvod dostiže maksimum.
1
Uslov «bez menjanja bilo čega drugog» je u ekonomiji jako važan i naziva se
«ceteris paribus».
8
Želiš da pročitaš svih 27 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































