studenti.rs home page

Pronalaženje ekstrema funkcija dvije promjenjive 

uz pomo

ć

 MatLab-a 

 

 

Zadatak broj 1 

 
Na

ć

i ekstreme funkcije 

y

e

y

x

z

)

(

2

+

=

. 

 
 
Rj. 
 

>> syms x y 
>> f=(x^2+y)*sqrt(exp(y)) 
  
f = 
  
(x^2+y)*exp(y)^(1/2) 
  
>> pretty(f) 
  
                                2            1/2 
                              (x  + y) exp(y) 
>> 
 

Na

đ

imo prve parcijalne izvode. 

 
>> fx=diff(f,x); 
>> fx=simple(fx); 
>> pretty(fx) 
  
                                           1/2 
                                 2 x exp(y) 
>> fy=diff(f,y); 
>> fy=simple(fy); 
>> pretty(fy) 
  
                                    1/2       2 
                          1/2 exp(y)    (2 + x  + y) 
>> 
 

Riješimo sistem jedna

č

ina. 

 
>> [a,b]=solve(fx,fy); 
>> double([a,b]) 
 
ans = 
 
     0    -2 
 

 
Stacionarna ta

č

ka je M(0,-2). Na

đ

imo druge parcijalne izvode. 

 
>> fxx=diff(fx,x); 
>> fxx=simple(fxx); 
>> pretty(fxx) 
  
                                          1/2 
                                  2 exp(y) 
>> fxy=diff(fx,y); 
>> fxy=simple(fxy); 
>> pretty(fxy) 
  
                                          1/2 
                                  x exp(y) 
>> fyy=diff(fy,y); 
>> fyy=simple(fyy); 
>> pretty(fyy) 
  
                                    1/2       2 
                          1/4 exp(y)    (4 + x  + y) 
>> 
 

Definišimo D i izra

č

unajmo vrijednost u ta

č

ki M(0,-2).

 

 
>> D=fxx*fyy-(fxy)^2; 
>> subs(D,[x,y],[0,-2]) 
 
ans = 
 
    0.1353 
 

Kako je D>0 funkcija u ta

č

ki M ima ekstrem. Prona

đ

imo vrijednost od A.

 

 
>> subs(fxx,[x,y],[0,-2]) 
  
ans = 
  
2*exp(-2)^(1/2) 
 

Vidimo da je A>0.

 

 
>> subs(f,[x,y],[0,-2]) 
 
ans = 
 
   -0.7358 
 
 

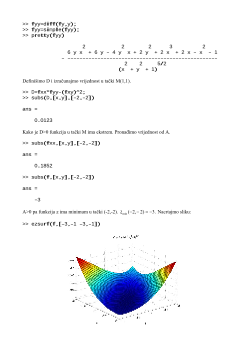
Prema tome funkcija z ima minimum u ta

č

ki (0,-2). 

7358

,

0

)

2

,

0

(

min

−

=

−

z

. Nacrtajmo sliku:

 

 
 

background image

Želiš da pročitaš svih 7 strana?

Prijavi se i preuzmi ceo dokument.

Prijavi se Napravi nalog

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.

Slični dokumenti