
Proračun AB konstrukcije Pregled
Završni rad
Ivan Filipović
I
Sadržaj:
1.
Uvod
1
2.
Tlocrti,
presjeci
i pročelja objekta
3
2.1.
Tlocrt karakterističnog
1. kata (MJ 1:50)
4
2.2.
Tlocrt krovnih ploha (MJ 1:50)
5
2.3.
Uzdužni presjek karakterističnog
1. kata (MJ 1:50)
6
2.4.
Poprečni presjek karakterističnog
1. kata (MJ 1:50)
7
2.5.
Sjeverozapadno
i jugozapadno pročelje
(MJ 1:50)
8
3.
Tehnički opis
9
3.1.
Lokacija
10
3.2.
Konstr
u
kcija
10
3.3.
Materijal za izradu konstrukcije
11
3.4.
Primijenjeni propisi
11
4.
Model konstrukcije
12
4.1.
Opis modela
13
4.2.
Perspektivni prikaz modela konstrukcije
14
4.3.
Tlocrti etaža
19
4.4.
Presjeci po osima
23
5.
Opterećenje konstrukcije
25
5.1.
Analiza opterećenja
26
5.1.1.
Opterećenje vlastitom težinom
26
5.1.2.
Stalno opterećenje
26
5.1.3.
Uporabno opterećenje
27
5.1.4.
Opterećenje snijegom
28
5.1.5.
Opterećenje potresom
28
5.2.
Kombinacije opterećenja
29
6.
Kvazistatička analiza proračuna
na potres
33
6.1.
Proračunsko ubrzanje tla
34
6.2.
Faktori važnosti zgrade
35
6.3.
Razred tla
35
6.4.
Razred duktilnosti
36
6.5.
Provjera pravilnosti građevine
36
6.6.
Faktori ponašanja
36
6.7.
Proračunski spektar odaziva
38
6.8.
Prikaz izlaznih rezultata modalne analize
40
7.
Pomaci konstrukcije
45
7.1.
Proračun pomaka konstrukcije i rezultati proračuna
46
7.2.
Provjera ograničenja međukatnog pomaka
46
Završni rad
Ivan Filipović
II
8.
Unutarnje sile i dimenzioniranje
48
8.1.
Uvod
49
8.2.
Stup C
-8
, prizemlje
50
8.2.1.
Presjek dolje
53
8.2.2.
Presjek gore
55
8.3.
Greda
B106, prizemlje
57
8.3.1.
Dimenzioniranje na moment savijanja
61
8.3.2.
Dimenzioniranje na poprečne sile
64
8.4.
Plan armature stupa i grede
65
9.
Komentar provedene analize
68
9.1.
Osvrt na rezultate analize
69
9.2.
Prijedlog promjene postojećeg stanja
69
10.
Literatura
73
Završni rad
Ivan Filipović
2
U završnom radu se obraduje statička analiza objekta nepravilnih tlocrtnih dimenzija
površine 800 m
2
. Objekt je visok
11,06
m iznad kote terena, te ima ukupno
P+2
etaž
e
. Nacrti
karakterističnog kata,
presjeci i pročelja
su dani u
poglavlju 2
. Konstrukcija se
nalazi u
seizmi
čki aktivnom području, pa je posebno analizirano ponašanje
konstrukcije pri potresnom
optere
ć
enju.
Tehnički opis konstrukcije, materijali za izradu konstrukcije i propisi koji su korišteni
u završnom radu obrađeni su u
poglavlju 3.
Numerički
model konstrukcije i
zra
đ
en je u programu
Etabs Nonlinear 9.0.4.
Model je
detaljnije opisan u
poglavlju 4
. Na njemu je proveden stati
čki proračun. Zbog složenosti
modela, rezultati su prikazani na karakteristič
nim
dijelovima konstrukcije. Priloženi nacrti
izra
đ
eni su u programu
AutoCAD 2008.
Ulazni podaci i rezultati proračuna u radu su prikazani tablič
no i grafi
čki, te detaljno
objašnjeni.
Analiza opterećenja i mjerodavne kombinacije koje su korištene u proračunu obrađene
su u
poglavlju 5.
Seizmi
čki proračun konstrukcije prema
Eurocodeu 8
i interpretacija dobivenih
rezultata su prikazani u
poglavlju 6
.
U
poglavlju 7
su analizirani
maksimalni pomaci konstrukcije i
relativni pomaci
katova.
U
poglavlju 8
provedeno je dimenzioniranje
za odabrane elemente konstrukcije:
stup
C-8 i dio greda B106.
U
poglavlju 9
dan je
k
rat
k
i
k
omentar na provedenu ana
l
izu i prijed
l
og promjene
postoje
ć
eg stanja u vidu pobo
l
jšanja stati
čk
i
h
i dinami
čk
i
h
uvjeta.
Završni rad
Ivan Filipović
3
2.
Tlocrti, presjeci i pročelja objekta

Završni rad
Ivan Filipović
10
3.1.
Lokacija
Više
stambena
građevina smještena je uz Partizansku ulicu na k.č.
3901/40,
k.o. Poreč.
Ulaz u građevinu, kako za stanare, tako i za osobna vozila osigurani su iz novoizgrađene ulice
koja prolazi sa sjeveroistočne strane građevine. U odnosu na relativnu kotu ±o,o, vanjski
prostor za parkiranje nalazi se na koti
-
0,11, dok je pod garaže na koti
-
2,90. Prilaz stanovima
za stanare osiguran je vanjskim stepenicama dok je za invalidne osobe prilaz osiguran također
sa novoformirane ulice preko ulaza za osobna vozila.
3.2.
K
onstrukcija
Iz projektne dokumentacije također je vidljivo da je objekt konstruktivno koncipiran tako
da su mu poprečni zidovi (koji su na razmaku od 7,20m) te uzdužni zidovi izvedeni od
armiranoga betona debljine 16cm. Zidovi u suterenu su također od armiranoga betona
debljine 16 cm. Svi vanjski zidovi
su obrađeni toplinskom zaštitom i površinskom obradom
fasade koji će biti definirani u suglasnosti sa konzervatorskom službom.
Međukatna konstrukcija i stepeništa izvode se kao monolitna armirano
-
betonska ploča.
Stropovi su od knaufa ili betonski koji se žbukaju slojem grube i fine žbuke. Nakon gletanja
stropovi se liče vapnenom bojom. Završna obrada pod ova predviđa se od kamenih ploča,
keramike, parketa i tapisona.
Ploča poda podruma debljine je 17cm izvedena od armiranoga betona ispod koje dolazi
Voltex izolacija koja leži na betonskoj podlozi debljine 7cm. Iz uzdužnih i poprečnih presjeka
te iz izvršenih sondažnih jama iskop za podrum građevine izvest će se djelomično u glini, a
djelomično u kamenu vapnencu. Kako je iskop u glini dublji od potrebnog iskopa za podrum,
potrebno je glinu iskopati do zdravog tla, tj. do kamenoga sloja. Više iskopano, a do kote
betoniranja donje betonske podloge, ispuniti će se sa mršavim betonom (špar beton), to je
ispuna sa bilo kojim drugim materijalom nedozvoljena.
Temelje građevine obvezno temeljiti na kamenoj stijeni. Temelji su kontrolirani kao
ploča na elastičnim osloncima sa K
z
=16000,00 kN/m
3
. Naponi u tlu su od 200,00 do 320,0
0
kN/m
2
. Temelji ispod AB zidova su trakasti a ispod stupova temelji samci debljine 70 cm.
Dimenzije temelja vide se u arhitektonskom projektu
.
Ravne i kose međukatne ploče koje su debljine 20cm izvedene su od armiranoga betona,
kompletno sa glatkom oplatom i armaturom. Prema općim uvjetima i statičkom računu
izvoditelj radova dužan je prije početka radova pribaviti potrebne ateste o kvaliteti i čvrstoći
betona, armature i agregata, kao i sve elemente građevine koji zahtijevaju ateste o kakvoći
ugrađenoga materijala. Za sve ostale elemente ugradbe materijala
i
način ugradbe naznačeni
su u troškovniku građevinskih radova
.
Završni rad
Ivan Filipović
11
3.3.
Materijal za izradu konstrukcije
•
Materijal:
Beton C25/30 (MB 30)
Klasa betona C25/30
f
ck
-
tlačna čvrstoća
25 N/mm
2
E
cm
-
modul elastičnosti
30
500 N/mm
2
??
-
Poissonov koeficijent
0,2
Armatura B
-
500 (RA400/500)
Svojstvo
č
elika
f
u
-
vlačna čvrstoća
500
N/mm
2
f
y
-
granica popuštanja
400
N/mm
2
E -
modul elastičnosti
200000 N/mm
2
??
-
Poissonov koeficijent
0,3
3.4.
Primijenjeni propisi
•
HRN ENV 1990
•
HRN ENV 1991
o
HRN ENV 1991
-1
o
HRN ENV 1991
-2-1
o
HRN ENV 1991
-2-3
•
HRN ENV 1992
o
HRN ENV 1992
-1-1
•
HRN ENV 1998
o
HRN ENV 1998
-1-1
o
HRN ENV 1998
-1-2
o
HRN ENV 1998
-1-3

Završni rad
Ivan Filipović
13
4.1.
Opis modela
Numeri
č
ki model konstrukcije za potrebe stati
č
kog prora
č
una izra
đ
en je programom
Etabs Nonlinear 9.0.4
. S obzirom da je provedena analiza objekta na djelovanje seizmi
č
kog
optere
ć
enja, u kojoj svaki dio konstrukcije daje svoj doprinos, napravljen je model cijele
konstrukcije.
Model konstrukcije ne sadrži stubišta i neopterećene stupove koji služe radi
postizanja vizualnog dojma, ali su njihova opterećen
ja uzeta u obzir.
Radi ograničenosti
vremenom u nije uzeta u obzir podzemna garaža već je postavljena samo temeljna ploča.
Samo takvim modelom se može dovoljno točno približiti stvarnom
ponašanju konstrukcije.
Trodimenzionalni model konstrukcije prikazan u
točci 4.2.
Položaj osi modela preuzet je iz
izvedbenog projekta konstrukcije i prikazan je
u točkama
4.3. i 4.4.
Plošni elementi u modelu su definirani kao konač
ni elementi ljuske (engl.
shell
) elementi.
Pod plošne elemente spadaju ploč
e i zidovi. Veli
či
na kona
č
nih elemenata plo
č
a i zidova je
ograni
č
ena s pozicijama drugih elemenata koji zadiru u njih, te raznim otvorima. Kod svih
plo
č
a i zidova
je korištena
funkcija automatskog dijeljenja elemenata na manje
(1x1 m) kako
bi se što toč
nije dobile lokalne nepravilnosti i koncentracije naprezanja.
Štapni elementi (engl.
frame element
) su koriš
teni za stupove.
Svim štapnim elementima
su
pridruženi odgovarajući
popre
č
ni presjeci.
Tlo je modelirano kao Winklerova podloga s koeficijentom posteljice
??
??
= 16000,00
????
/
??
3
u smjeru osi Z. To
č
kama temeljne plo
č
e sprije
č
eni su pomaci u dva
horizontalna smjera X i Y, te sva tri stupnja rotacije.
Od optere
ć
enja na konstrukciju
nije uzeto u razmatranje vjetrovno opterećenje jer je
konstrukcija armirano-betonska pa ono nema utjecaja. Ostala
opterećenja
su zadana prema
poglavlju 6.
Zbog složenosti modela konstrukcije,
i ograničenosti predznanjem
rezultati
prora
č
una nisu prikazani u cijelosti, ve
ć
su izdvojeni oni podatci koji su od zna
č
aja za
prora
č
un konstrukcij
e i oni su objašnjeni u radu
.
Završni rad
Ivan Filipović
14
4.2.
Perspektivni prikaz modela konstrukcije
Slika 4.1. Perspektiva s prednje strane

Završni rad
Ivan Filipović
16
Slika 4.3. Pogled s prednje strane
Završni rad
Ivan Filipović
17
Slika 4.4.
Pogled s bočne strane

Završni rad
Ivan Filipović
19
4.3.
Tlocrti etaža
Slika 4.6. Tlocrt temeljne ploče
Završni rad
Ivan Filipović
20
Slika 4.7. Tlocrt ploče prizemlja

Završni rad
Ivan Filipović
22
Slika 4.9
. Tlocrt ploče 2. kata
Završni rad
Ivan Filipović
23
4.4.
Presjeci po osima
Slika 5.0. Presjek 1-1
Slika 5.1. Presjek 5-5
Slika 5.
2
. Presjek A-A

Završni rad
Ivan Filipović
25
5.
Opterećenje konstrukcije
Završni rad
Ivan Filipović
26
5.1.
Analiza opterećenja
5.1.1.
Opterećenje vlastitom težinom
Djelovanje vlastite težine elemenata definirano je propisima:
HRN ENV 191-2-1: Osnove projektiranja i djelovanja na konstrukcije.
Prostorne težine, vlastita težina i uporabna opterećenja. Točka 5.
Za zadane poprečne presjeke greda, stupova, stropova i zidova program
Etabs Nonlinear
9.0.4.
izravno računa opterećenje vlastitom težinom. Taj je slučaj
opterećenja definiran s:
VT
.
Budući da stubišta nisu
modelirana u modelu objekta, u
VT
je dodano
opterećenje od
konstrukcije stubišta i stupova.
•
Stubište
??
= 12211,19
????
2
-
površina poprečnog presjeka stubišta
??
= 580
????
-
duljina stubišta
??
=
??
??
= 21,1
????
-
srednja debljina ploče stubišta
??
??
= 25
????
/
??
3
-
zapreminska težina betona
????
??????????
š
????
=
??
??
∙ ??
= 25
∙
0,211 = 5,28
????
/
??
2
•
Stupovi
??
= 0,155
??
3
-
Volumen stupa
??
??
= 25
????
/
??
3
-
zapreminska težina betona
????
??????????
=
??
??
∙ ??
= 25
∙
0,211 = 3,88
????
5.1.2.
Stalno opterećenje
Djelovanje vlastite težine elemenata definirano je propisima:
HRN ENV 191-2-1: Osnove projektiranja i djelovanja na konstrukcije.
Prostorne težine, vlastita težina i uporabna opterećenja. Točka 5.

Završni rad
Ivan Filipović
28
5.1.4.
Opterećenje snijegom
Djelovanje opterećenja snijegom definirano je propisima:
HRN ENV 191-2-3: Osnove projektiranja i djelovanja na konstrukcije.
Opterećenje od snijega. Točka 6.
Opterećenje snijegom u programu
Etabs Nonlinear 9.0.4.
definirano je sa:
SNIJEG
. Na
krovnim pločama zgrade zadano je jednoliko kontinuirano opterećenje snijegom prema
propisima:
??
??
= 0,35
????
/
??
2
5.1.5.
O
pterećenje
potresom
Djelovanje opterećenja potresom definirano je propisima:
HRN ENV 1998: Osnove Projektiranja konstrukcija otpornih na potres.
Opterećenje potresom je definirano na temelju analize u točci 6. Opterećenje potresom u
programu
Etabs Nonlinear 9.0.4.
zadano je kao opterećenje i nazvano:
POTRES
.
Završni rad
Ivan Filipović
29
5.2.
Kombinacije opterećenja
Izrazi kombinacija opterećenja za krajnje granično stanje i za granično stanje
uporabivosti
definirani su propisima:
HRN ENV 1991-1: Osnove projektiranja i djelovanja na konstrukcije.
Osnove prora
čuna. Toč
ka 9.
Granična stanja nosivosti (GSN)
Za svaki kritičan slučaj opterećenja računske vrijednosti utjecaja djelovanja
moraju se
odrediti kombiniranjem vrijednosti djelovanja koja nastaju istovremeno.
•
trajne i prolazne proračunske situacije (KGS)
��??
??
,
??
∙ ??
??
,
??
�
" + "
??
??
,1
∙ ??
??
,1
"
?? ≥
1
+
��??
??
,
??
∙ Ψ
0,
??
∙ ??
??
,
??
�
"
??≥
1
"
U slučaju konstrukcija zgrada dozvoljeno je primijeniti sljedeć
e
pojednostavljene izraze:
� ??
??
,
??
∙ ??
??
,
??
?? ≥
1
" + "[1,5]
∙ ??
??
,1
� ??
??
,
??
∙ ??
??
,
??
?? ≥
1
" + "[1,35]
∙ � ??
??
,
??
?? ≥
1
•
seizmičke
proračunske situacije (KGS)
� ??
??
,
??
?? ≥
1
" + "
??
??
∙ ??
????
" + "
��Ψ
2,
??
∙ ??
??
,
??
�
"
??≥
1
"

Završni rad
Ivan Filipović
31
Na modelu zadani su sljedeći slučajevi opterećenja:
•
vlastita težina
VT
(G)
•
dodatno stalno opterećenje
STALNO
(G)
•
korisno opterećenje
POKRETNO
(Q)
•
opterećenje snijegom
SNIJEG
(S)
•
djelovanje statičkog potresa u smjeru X
POTRESX
(A)
•
djelovanje statičkog potresa u smjeru Y
POTRESY
(A)
U
skladu s navedenim pravilima definirane su sljedeće kombinacije opterećenja:
•
Osnovna kombinacija za granično stanje uporabivosti
(DEFORM)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 1,0
∙
(
????????????????
)
•
Mjerodavne kombinacije za granično stanje uporabivosti
(DIMENZ1)
1,35
∙
(
????
) + 1,35
∙
(
????????????
) + 1,5
∙
(
????????????????
)
(DIMENZ
2
)
1,35
∙
(
????
) + 1,35
∙
(
????????????
) + 1,5
∙
(
????????????
)
(DIMENZ3)
1,35
∙
(
????
) + 1,35
∙
(
????????????
) + 1,35
∙
(
????????????????
) + 1,5
∙
(
????????????
)
(DIMENZ4)
1,35
∙
(
????
) + 1,35
∙
(
????????????
)
(SEIZMIKA1)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
)
(SEIZMIKA2)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
)
(SEIZMIKA3)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
)
(SEIZMIKA4)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
)
(SEIZMIKA5)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
) + 0,3 (
??????????????
)
Završni rad
Ivan Filipović
32
(SEIZMIKA6)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
) + 0,3 (
??????????????
)
(SEIZMIKA7)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
)
−
0,3 (
??????????????
)
(SEIZMIKA8)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
)
−
0,3 (
??????????????
)
(SEIZMIKA9)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
) + 0,3 (
??????????????
)
(SEIZMIKA10)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
) + 1,0
∙
(
??????????????
)
−
0,3 (
??????????????
)
(SEIZMIKA 11)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
) + 0,3 (
??????????????
)
(SEIZMIKA 12)
1,0
∙
(
????
) + 1,0
∙
(
????????????
) + 0,3
∙
(
????????????????
)
−
1,0
∙
(
??????????????
)
−
0,3 (
??????????????
)

Završni rad
Ivan Filipović
34
6.1.
Proračunsko ubrzanje tla
(HRN ENV 1998-1-
1, NAD, tablica NAD.1)
Prema
Eurocode
-
u
8
svaka zemlja u kojoj se on primjenjuje mora biti podijeljena na
seizmičke zone
ovisno o tektonskim svojstvima. Zbog toga svaka država
mora za određeno
područje primjene propisa
Eurocode
-
a propisati svoje specifičnosti
donošenjem posebnih
dokumenata (engl.
National Application Document
–
NAD
).
Ovisno o seizmičkoj zoni, u
NAD
-
u je definirana vrijednost maksimalnog ubrzanja
a
g
u
stjenovitom ili zbijenom tlu, koje je idealno za temeljenje građevina u seizmičkim
područjima. Seizmička karta za Republiku Hrvatsku je prikazana na slici 7.1
Slika 6.1. –
Seizmička karta Republike Hrvatske
Završni rad
Ivan Filipović
35
Potresno djelovanje određuje se preko proračunskog ubrzanja tla
a
g
,
koje odgovara povratnom
periodu potresa od 500 godina.
P
roračunsko ubrzanja tla
a
g
za različita potresna područja
dano
je tablicom
7.1
.
Područje intenziteta
potresa u stupnjevima
MKS-64
Proračunsko ubrzanje tla
Proračunsko ubrzanje tla
6
0,05g
0,5 m/s
2
7
0,1g
1,0 m/s
2
8
0,2g
2,0 m/s
2
9
0,3g
3,0 m/s
2
Tablica 6
.1. -
Proračunsko ubrzanja tla
a
g
za različita potresna područja
Za grad Poreč iz karte 7.1. očitano je da je intenz
i
tet potresa 7, a
tablice 7.1. za taj
intenzitet očitano je proračunsko ubrzanje:
??
??
= 0,1
??
,
??
??
= 1,0
??
/
??
2
6.2.
Faktori važnosti zgrade
(HRN ENV 1998-1-2
, NAD, tablica NAD.1)
Prema namjeni,
z
grada
pripada u klasu
III
. Zgrada je namijenjena za stambeno
-
poslovne
prostore.
Faktor važnosti zgrade:
??
??
= 1,0
6.3.
Razred tla
(HRN ENV 1998-1-1,
točka 3)
Tlo je svrstano u razred
A
.
Razred
A
predstavlja stjenovita tla s brzinom širenja poprečnih valova
??
??
≥
800
??
/
??
,
pjeskovita i šljunkovita tla s
??
??
≥
400
??
/
??
na dubini od 10m.

Završni rad
Ivan Filipović
37
Dan je izrazom:
??
=
??
0
∙ ??
??
∙ ??
??
∙ ??
??
≥
1,5
gdje
je:
??
0
-
osnovna vrijednost faktora ponašanja (tablica 7.2.)
za zidni sustav s povezanim zidovima
??
0
= 5,0
Vrsta konstrukcije
??
??
Okvirni sustav
5,0
Dvojni sustav
Istovrijedan okvirnom
5,0
Istovrijedan zidom s povezanim zidovima
5,0
Istovrijedan zidom s nepovezanim zidovima
4,5
Zidni sustav
s povezanim zidovima
5,0
s nepovezanim zidovima
4,0
Sustav s jezgrom
3,5
Sustav obrnutog njihala
2,0
Tablica 6
.2. –
Osnovne vrijednosti faktora ponašanja
??
??
-
faktor koji odražava razred duktilnosti
z
a srednju klasu duktilnosti DC «
M
»,
??
??
= 0,75
??
??
-
faktor koji odražava pravilnost konstrokcije po visini
za pravilne konstrukcije po visini
??
??
= 1,0
??
??
-
faktor koji odražava prevladavajući oblik sloma konstrukcijskog sustava zidova
.
Za zidne sustave, za dvojne sustave istovrijedne zidnim i sustave s jezgrom je
definiran kao:
??
??
=
1
2,5
−
0,5
∙ ??
0
≤
1
gdje je:
??
0
-
prevladavajući koeficijent oblika
??
0
=
∑ ??
????
∑ ??
????
??
????
-
visina zida
i
??
????
-
duljina presjeka zida
i
??
0
=
∑ ??
????
∑ ??
????
,
??
??
=
1
2,5
−
0,5
∙ ??
0
≤
1
??
??
=
1
2,5
−
0,5
∙ ??
0
≤
1
??
??
= 1
Završni rad
Ivan Filipović
38
Faktor ponašanja
q:
??
=
??
0
∙ ??
??
∙ ??
??
∙ ??
??
≥
1,5
??
= 5,0
∙
0,75
∙
1,0
∙
1,0
≥
1,5
??
= 3,75
≥
1,5
Vertikalna potresna djelovanja
Za vertikalnu komponentu potresnog djelovanja faktor ponašanja
q
općenito je 1,0 za sve
konstrukcijske sustave.
6.7.
Proračunski spektar odaziva
Da bi se izbjegla opsežna nelinearna analiza sustava, uzima se u obzir mogućnost
disperzije energije
konstrukcije
preko duktilnosti njezinih elemenata.
Parametri za definiranje elastičnog spektra titranja
??
??
(
??
)
dani su tablicom 7.3.
Razred
tla
S
??
??
??
??
??
??
??
??
(
??
)
??
??
(
??
)
??
??
(
??
)
A
1,0
2,5
1,0
2,0
0,10
0,4
3,0
B
1,0
2,5
1,0
2,0
0,15
0,6
3,0
C
0,9
2,5
1,0
2,0
0,20
0,8
3,0
Tablica
6.3. –
Vrijednosti parametara koje opisuju elastični spektar titranja
Proračunski spektar odziva
??
??
(
??
)
dobiva se iz elastičnog njegovom redukcijom uz pomoć
faktora ponašanja q u kombinaciji s modificiranim eksponentima
koji
su dani tablicom 7.
4.
Razred tla
??
????
??
????
A
2/3
5/3
B
2/3
5/3
C
2/3
5/3
Tablica
6.4. –
Vrijednosti parametara
??
????
i
??
????

Završni rad
Ivan Filipović
40
6.8.
Prikaz izlaznih rezultata modalne analize
Neki izlazni podaci iz programa
Etabs Nonlinear 9.0.4
, u kojem je rađena
analiza
konstrukcije, prikazani su tablično. Zbog velike količine podataka i što
jednostavnijeg
prikaza, rezultati su obrađeni i sažeti. Izdvojeni su oni podatci koji su
od najvećeg značaja za
razumijevanje
ponašanja konstrukcije.
Na slikama 6
.2., 6.
3. i 6
.4.
prikazani su prvi, drugi i treći oblik osciliranja. Iz
slika je
vidljivo da prvom vlastitom obliku pripada dominantna translacija oko duže osi građevine
. Za
drugi vlastiti oblik je dominantna translacija
oko kraće osi građevine. Treći vlastiti oblik ima
značajan utjecaj rotacije oko osi Z. Taj torzijski
efekt trebalo bi izbjegavati u prvim tonovima.
Ovdje
je dominantan
u trećem tonu,
što je dobro
.
Ovi zaključci su jasnije vidljivi iz priloženih tablica 6.5, 6.6 i 6.7, koji nam daju
potrebnu
informaciju o ponašanju modelirane konstrukcije
.
•
Faktor doprinosa oblika osciliranja (engl.
Modal Participation Factors)
Mode
Period
UX
UY
UZ
RX
RY
RZ
ModalMass
ModalStiff
1
0,16
-38,08
-43,52
0,00
302,47
-257,9
54,22
1,00
1497,86
2
0,12
-43,28
37,15
0,00
-256,76
-291,9
-141,9
1,00
2590,11
3
0,11
5,36
-10,15
0,00
72,04
37,68
-651,1
1,00
3559,13
4
0,06
-0,33
1,53
0,00
-2,44
-2,31
11,03
1,00
9493,80
5
0,06
-0,04
-0,26
0,00
-0,52
0,46
16,48
1,00
9633,29
6
0,06
-0,04
-0,94
0,00
-0,07
-0,34
-8,69
1,00
9638,89
7
0,06
-0,06
-1,63
0,00
-0,24
-0,25
-8,24
1,00
9641,97
8
0,06
-0,03
-0,94
0,00
0,14
-0,25
-12,44
1,00
9658,46
9
0,06
0,05
1,47
0,00
0,00
0,27
-8,35
1,00
9662,62
10
0,06
-0,74
1,60
0,00
-5,40
2,34
56,03
1,00
10330,02
11
0,06
-0,07
-0,28
0,00
3,76
-0,31
-72,64
1,00
12522,75
12
0,04
0,27
0,02
0,00
0,29
0,60
-56,39
1,00
26796,11
Tablica 6.3.
–
Faktor doprinosa oblika osciliranja
(engl.
Modal Participation Factors)
Završni rad
Ivan Filipović
41
•
Omjer
doprinosa modalnih opterećenja (enl.
Modal Load Participation Ratios)
Type
Load
Accel
Story
Link
DOF
StatPercent
DynPercent
Load
VT
0,11
0,00
Load
STALNO
0,32
0,28
Load
POKRETNO
0,18
10,81
Load
SNIJEG
1,87
1,48
Load
POTRESX
99,98
98,19
Load
POTRESY
99,98
98,33
Accel
UX
99,08
50,56
Accel
UY
99,25
51,11
Accel
UZ
0,00
0,00
Accel
RX
101,46
99,81
Accel
RY
98,53
99,52
Accel
RZ
126,17
49,43
Tablica 6.3.
–
Omjer doprinosa modalnih opt. (engl.
Modal Load Participation Ratios)
•
Faktor
doprinosa modalnih masa (engl.
Modal Participation Mass Ratios)
Mode
Period
UX
UY
UZ
RX
RY
RZ
1
0,1623 21,87 28,56 0,00 56,14 43,22 0,32
2
0,1235 28,25 20,81 0,00 40,45 55,37 2,17
3
0,1053 0,43
1,55 0,00 3,18
0,92 45,62
4
0,0645 0,00
0,04 0,00 0,00
0,00
0,01
5
0,0640 0,00
0,00 0,00 0,00
0,00
0,03
6
0,0640 0,00
0,01 0,00 0,00
0,00
0,01
7
0,0640 0,00
0,04 0,00 0,00
0,00
0,01
8
0,0639 0,00
0,01 0,00 0,00
0,00
0,02
9
0,0639 0,00
0,03 0,00 0,00
0,00
0,01
10
0,0618 0,01
0,04 0,00 0,02
0,00
0,34
Tablica 6.4
. –
Faktor
doprinosa modalnih masa (engl.
Modal Participation Mass Ratios)

Završni rad
Ivan Filipović
43
Slika 6.3
. –
Drugi mod
(T
2
=0,1235)
Završni rad
Ivan Filipović
44
Slika 6.4
. –
Treći mod (torzija
T
3
=0,1053)

Završni rad
Ivan Filipović
46
7.1.
Proračun pomaka konstrukcije i rezultati proračuna
Relativni i apsolutni pomaci konstrukcije su dobiveni u obliku izlaznih
rezulta
ta
programa
Etabs Nonlinear 9.0.4.
Prikazani su u tablicama za mjerodavnu
kombinaciju optereć
enja
(
ANVELOPA
). Zbog velike količine podataka koje sadrže
izlazni podaci vezani za pomake
(engl.
Dispacements
), ovdje su prikazani samo oni
koji su bitni za provjeru globalnih pomaka
konstrukcije, i ti podaci ć
e se kasnije koristiti.
Ma
ksimalni relativni pomaci katova (engl.
story drift
) za kombinaciju
optereć
enja
(
ANVELOPA
) su prikazani u tablici 5.1
Story
Item
Load
Point
X
Y
Z
DriftX
DriftY
STORY4 Max Drift X ANVELOPA 782 18,13 3,56 11,07 0,000075
STORY4 Max Drift Y ANVELOPA 381
7,37 22,24 11,07
0,000131
STORY3 Max Drift X ANVELOPA 166
0
13,52 8,39
0,00014
STORY3 Max Drift Y ANVELOPA 239 21,63
9,2
8,39
0,000124
STORY2 Max Drift X ANVELOPA 273 10,65 25,8
5,56
0,00008
STORY2 Max Drift Y ANVELOPA
28
0
16,6
5,56
0,000089
STORY1 Max Drift X ANVELOPA 296
0
27,85 2,73 0,000087
STORY1 Max Drift Y ANVELOPA 164
0
9,2
2,73
0,000096
Tablica 7.1. – Maksimalni pomaci katova konstrukcije
7.2.
Provjera ograničenja međukatnog pomaka
Smatra se da je zahtjev za ograničenim oštećenjem pri potresu zadovoljen ako su
međukatni pomaci ograničeni (engl.
story drift
).
Ograničenje relativnog katnog pomaka za zgrade koje imaju za konstrukciju
pričvršć
ene
nekonstrukcijske elemente od krhkih gradiva dano je izrazom:
??
??
??
≤
0,002
∙ ℎ
,
(izmjene prema HRN ENV 1998
-1-
2, NAD 8)
gdje je:
d
r
-
pomak točke konstrukcijskog sustava zbog proračunskoga
potresnog djelovanja,
??
??
=
??
??
∙ ??
??
∙ ??
??
d
e
-
relativni pomak iste točke konstrukcijskog sustava određen linearnim
prorač
unom
utemeljenim na proračunskom spektru. Ovdje je očitan iz
kombinacije opterećenja za
potresno djelovanje
ANVELOPA
i iznosi:
de
=0,000131 m
–
maksimalni relativni pomak za smjer Y
ANVELOPA
, kat 4,
tablica 7
.1.
??
-
faktor važnosti (
??
= 1,0
),
q
d
-
faktor ponašanja za pomak koji je jednak q (q
d
=
3,75)
Završni rad
Ivan Filipović
47
Iz toga je relativni pomak točke konstrukcijskog sustava zbog proračunskoga
potresnog
djelovanja:
??
??
= 3,75
∙
0,000131
∙
1,0 = 0,00049
??
h
-
katna visina za mjerodavni kat ( h = 2,80
m ),
??
-
faktor redukcije kojim se uzima u obzir niži povratni period seizmičkog
događ
aja
koji se odnosi na granično stanje uporabljivosti. Faktor redukcije
zavisiti od važnosti
zgrade.
(
??
= 1,0
-
HRN ENV 1998
-1-
2, NAD 7)
0,00049
1
≤
0,002
∙
2,80
0,00049
?? ≤
0,0056
??
Relativni katni pomak zadovoljava propisane uvijete.

Završni rad
Ivan
Filipović
49
8.1.
Uvod
Dimenzioniranje je provedeno na temelju unutarnjih sila koje su dobivene linearnim
prora
č
unom modela konstrukcije. Kod dimenzioniranja konstrukcije korišten je programa
Etabs Nonlinear 9.0.4.
koji podržava dimenzioniranje po Eurocode
propisima. Rezultati
analize su dani kao površine armature u odre
đ
enom popre
č
nom presjeku. Potrebno je voditi
ra
č
una o vrijednostima minimalne i maksimalne armature u elementu.
Za potrebe ovog rada, zbog velikog opsega posla, provedeno je automatsko
dimenzioniranje cijele konstrukcije, ali su prikazani izlazni rezultati samo pojedinih
elemenata. To su bitni dijelovi konstrukcije kojima se daje uvid u dimenzioniranje cijele
konstrukcije.
Nadalje je provedena ručna ko
ntrola automatskog dimenzioniranja i to samo za jednu
gredu i jedan stup.
Također je priložen i nacrt armature
dimenzioniranih elemenata.
Dimenzioniranje je provedeno za sljedeće elemente
:
•
Stup C-8, prizemlje
•
Greda B106, prizemlje
Završni rad
Ivan
Filipović
50
8.2.
Stup C-8, prizemlje

Završni rad
Ivan
Filipović
52
Duljina stupa:
L= 283 cm
•
Duljina izvijanja stupa
Za duljinu izvijanja uzeta je ukupna duljina stupa, tj. nije rađen standardni postupak prema
Jackson - Morelandovim nomogramima. Razlog tome je što se smatra da je stup dio
nepomičnog okvira, a donji i gornji kraj je pridržan pločom. Pretpostavljajući zglo
bna
pridržanja na krajevima smo na strani sigurnosti, a budući da stup ima malenu vitkost, to
nema utjecaja na njegovu stabilnost i daljnji
proračun.
Moment inercije:
??
??????
=
??∙ℎ
3
12
= 312500
????
4
??
= 1,00
Duljina izvijanja:
??
??
=
?? ∙ ??
= 283
∙
1,00 = 283
????
Vitkost stupa:
??
=
??
??
??
??????
=
283
0,289
∙
50
= 19,58
•
Svojstva materijala i dimenzije stupa:
Materijal:
Beton: C25/30
Čelik:
B 500
Poprečni presjek:
30/50 cm
Visina presjeka:
h = 50 cm
Zaštitni sloj betona:
c = 3 cm
Udaljenost do težišta
armature:
d
1
= 4 cm
Statička visina presjeka:
d = h - d
1
= 50 – 4 = 46 cm
f
cd
–
računska čvrstoća betona
??
????
=
??
????
??
??
=
25
1,5
= 16,67
??
/
????
2
= 1,667
????
/
????
2
f
yd
–
računska granica popuštanja čelika
??
????
=
??
????
??
??
=
500
1,15
= 434,78
??
/
????
2
= 43,478
????
/
????
2
Završni rad
Ivan
Filipović
53
8.2.1.
Presjek dolje
Kombinacija:
DIMENZ1
??
????
= 21,44
??????
??
????
1
= 185,08
????
Bezdimenzionalni koeficijenti:
??
????
=
??
????
?? ∙ ??
2
∙ ??
????
=
2084
30
∙
46
2
∙
1,667 = 0,02
??
????
1
=
??
????
1
?? ∙ ?? ∙ ??
????
=
19152
30
∙
46
∙
43,478 = 0,308
•
Ograničenje
dijagrama interakcije:
Za razred duktilnosti
M
:
??
????
≤
0,65
∙ ?? ∙ ℎ ∙ ??
????
??
????
≤
0,65
∙
30
∙
50
∙
1,667
185,08
≤
1625,33
??
????
≤
0,65
0,9
0,308
≤
0,722
??
??????
= 0,043
??
??????
= 0,0222
∙
??
????
??
????
= 0,579
Dijagrami interakcije za:
??
= 1,00
-
simetrična armatura
??
1
/
ℎ
=
??
2
/
ℎ
= 0,1
Čelik:
B 500
Mehanički koeficijent armiranja
Očitano:
??
= 0,05
Potrebna površina armature:
??
??
1
=
??
??
2
=
?? ∙
??
????
??
????
∙ ?? ∙ ??
= 0,05
∙
1,667
43,478
∙
30
∙
46 = 2,65
????
2

Završni rad
Ivan
Filipović
55
8.2.2.
Presjek gore
Kombinacija:
DIMENZ1
??
????
= 7,68
??????
??
????
1
= 170,76
????
Bezdimenzionalni koeficijenti:
??
????
=
??
????
?? ∙ ??
2
∙ ??
????
=
703
30
∙
46
2
∙
1,667 = 0,007
??
????
1
=
??
????
1
?? ∙ ?? ∙ ??
????
=
17719
30
∙
46
∙
43,478 = 0,284
•
Ograničenje dijagrama interakcije:
Za razred duktilnosti
M
:
??
????
≤
0,65
∙ ?? ∙ ℎ ∙ ??
????
??
????
≤
0,65
∙
30
∙
50
∙
1,667
170,76
≤
1625,33
??
????
≤
0,65
0,9
0,284
≤
0,722
??
??????
= 0,043
??
??????
= 0,0222
∙
??
????
??
????
= 0,579
Dijagrami interakcije za:
??
= 1,00
-
simetrična armatura
??
1
/
ℎ
=
??
2
/
ℎ
= 0,1
Čelik:
B 500
Mehanički koeficijent armiranja
Očitano:
??
= 0,05
Potrebna površina armature:
??
??
1
=
??
??
2
=
?? ∙
??
????
??
????
∙ ?? ∙ ??
= 0,05
∙
1,667
43,478
∙
30
∙
46 = 2,65
????
2
Završni rad
Ivan
Filipović
56
Minimalna armatura:
??
??
,
??????
= 0,15
∙
??
????
??
????
= 0,15
∙
170,76
43,478
= 0,59
????
2
(1) uvjet
??
??
,
??????
= 4
Φ
12 = 4,52
????
2
(2) uvjet
??
??
,
??????
= 0,003
∙ ??
??
= 0,003
∙
30
∙
50 = 4,5
????
2
(3) uvjet
??
??
,
??????
= 0,01
∙ ??
??
= 15
????
2
(4) uvjet
Maksimalna armatura:
??
??
,
??????
= 0,04
∙ ??
??
= 0,04
∙
30
∙
50 = 60
????
2
??
??
,
??????
= 0,08
∙ ??
??
= 0,08
∙
30
∙
50 = 120
????
2
Odabrana armatura mora se nalaziti u podru
č
ju izme
đ
u minimalne i maksimalne armature:
??
??
,
??????
≤ ??
??
≤ ??
??
,
??????
ODBRANO:
????????
�??
??
1,
????
= 8,04
????
2
�
Ukupna armatura:
??
??
= 8,04 + 8,04 = 16,08
????
2
??
??
,
??????
= 15
????
2
≤ ??
??
= 16,08
????
2
≤ ??
??
,
??????
= 60
????
2
Razmak vilica:
??
??
= 12
∙
Φ
??
,
??????
= 12
∙
2,5 = 30
????
(1) uvjet
??
??
=
??
= 50
????
(2) uvjet
??
??
= 30
(3) uvjet
??
??
= 15
- za srednju duktilnost „
M“
(4) uvjet
– ako stup preuzima sile potresa
ODBRANO:
????
/
????
????
U blizini ležaja vilice se progušćuju na
razmak
≤
0,6
∙ ??
??
(9 cm), na duljini:
??
= 1,5
∙ ??
= 1,5
∙
30 = 45
????
??
=
1
6
∙ ??
=
1
6
∙
238 = 39,67
????
??
= 35
????

Završni rad
Ivan
Filipović
58
Story
Beam Load
Loc
P
V2
V3
T
M2
M3
STORY2 B106 DEFORM
0 -0,51 -0,44 -0,02 -0,097 -0,004
0,11
STORY2 B106 DEFORM
0,323 -0,51
-0,3 -0,02 -0,097
0,003
0,23
STORY2 B106 DEFORM
0,645 -0,51 -0,16 -0,02 -0,097
0,009
0,305
STORY2 B106 DEFORM
0,645
0,21 -0,43
0
0,079
0 -0,407
STORY2 B106 DEFORM
1
0,21 -0,27
0
0,079
0 -0,282
STORY2 B106 DIMENZ1
0 -0,71 -0,61 -0,03 -0,133 -0,006
0,15
STORY2 B106 DIMENZ1
0,323 -0,71 -0,41 -0,03 -0,133
0,004
0,314
STORY2 B106 DIMENZ1
0,645 -0,71 -0,22 -0,03 -0,133
0,013
0,417
STORY2 B106 DIMENZ1
0,645
0,28 -0,59
0
0,109
0 -0,555
STORY2 B106 DIMENZ1
1
0,28 -0,37
0
0,109
0 -0,385
STORY2 B106 DIMENZ2
0 -0,58 -0,56 -0,03 -0,102 -0,005
0,132
STORY2 B106 DIMENZ2
0,323 -0,58 -0,36 -0,03 -0,102
0,003
0,28
STORY2 B106 DIMENZ2
0,645 -0,58 -0,17 -0,03 -0,102
0,012
0,366
STORY2 B106 DIMENZ2
0,645
0,31 -0,54
0
0,09 -0,001 -0,496
STORY2 B106 DIMENZ2
1
0,31 -0,32
0
0,09
0 -0,343
STORY2 B106 DIMENZ3
0 -0,69
-0,6 -0,03 -0,129 -0,006
0,149
STORY2 B106 DIMENZ3
0,323 -0,69 -0,41 -0,03 -0,129
0,004
0,313
STORY2 B106 DIMENZ3
0,645 -0,69 -0,22 -0,03 -0,129
0,013
0,414
STORY2 B106 DIMENZ3
0,645
0,31 -0,58
0
0,108
0 -0,552
STORY2 B106 DIMENZ3
1
0,31 -0,37
0
0,108
0 -0,383
STORY2 B106 DIMENZ4
0 -0,58 -0,55 -0,03 -0,104 -0,005
0,131
STORY2 B106 DIMENZ4
0,323 -0,58 -0,36 -0,03 -0,104
0,003
0,278
STORY2 B106 DIMENZ4
0,645 -0,58 -0,17 -0,03 -0,104
0,012
0,364
STORY2 B106 DIMENZ4
0,645
0,28 -0,53
0
0,088 -0,001 -0,492
STORY2 B106 DIMENZ4
1
0,28 -0,32
0
0,088
0 -0,341
STORY2 B106 SEIZMIKA1
0 -0,55 -0,42 -0,02 -0,083 -0,004
0,099
STORY2 B106 SEIZMIKA1
0,323 -0,55 -0,28 -0,02 -0,083
0,003
0,211
STORY2 B106 SEIZMIKA1
0,645 -0,55 -0,13 -0,02 -0,083
0,01
0,277
STORY2 B106 SEIZMIKA1
0,645
0,1
-0,4 -0,01
0,07 -0,002 -0,372
STORY2 B106 SEIZMIKA1
1
0,1 -0,24 -0,01
0,07
0,001 -0,257
STORY2 B106 SEIZMIKA2
0 -0,37 -0,42 -0,02 -0,083 -0,003
0,102
STORY2 B106 SEIZMIKA2
0,323 -0,37 -0,28 -0,02 -0,083
0,002
0,216
STORY2 B106 SEIZMIKA2
0,645 -0,37 -0,14 -0,02 -0,083
0,008
0,283
STORY2 B106 SEIZMIKA2
0,645
0,32 -0,41
0
0,069
0,001 -0,383
STORY2 B106 SEIZMIKA2
1
0,32 -0,25
0
0,069
0 -0,265
STORY2 B106 SEIZMIKA3
0 -0,66 -0,31 -0,02
-0,08 -0,004
0,046
STORY2 B106 SEIZMIKA3
0,323 -0,66 -0,17 -0,02
-0,08
0,003
0,123
STORY2 B106 SEIZMIKA3
0,645 -0,66 -0,02 -0,02
-0,08
0,009
0,154
STORY2 B106 SEIZMIKA3
0,645 -0,09 -0,25
0,01
0,069
0,002 -0,204
STORY2 B106 SEIZMIKA3
1 -0,09 -0,09
0,01
0,069 -0,001 -0,144
STORY2 B106 SEIZMIKA4
0 -0,25 -0,53 -0,02 -0,086 -0,004
0,155
STORY2 B106 SEIZMIKA4
0,323 -0,25 -0,39 -0,02 -0,086
0,002
0,304
STORY2 B106 SEIZMIKA4
0,645 -0,25 -0,25 -0,02 -0,086
0,008
0,407
STORY2 B106 SEIZMIKA4
0,645
0,51 -0,56 -0,01
0,07 -0,003 -0,551
Završni rad
Ivan
Filipović
59
STORY2 B106 SEIZMIKA4
1
0,51 -0,41 -0,01
0,07
0,001 -0,378
STORY2 B106 SEIZMIKA5
0 -0,61 -0,38 -0,02 -0,082 -0,004
0,083
STORY2 B106 SEIZMIKA5
0,323 -0,61 -0,24 -0,02 -0,082
0,003
0,184
STORY2 B106 SEIZMIKA5
0,645 -0,61
-0,1 -0,02 -0,082
0,01
0,239
STORY2 B106 SEIZMIKA5
0,645
0,01 -0,35 -0,01
0,07 -0,002
-0,32
STORY2 B106 SEIZMIKA5
1
0,01
-0,2 -0,01
0,07
0 -0,222
STORY2 B106 SEIZMIKA6
0 -0,43 -0,39 -0,02 -0,082 -0,003
0,086
STORY2 B106 SEIZMIKA6
0,323 -0,43 -0,25 -0,02 -0,082
0,002
0,189
STORY2 B106 SEIZMIKA6
0,645 -0,43 -0,11 -0,02 -0,082
0,008
0,246
STORY2 B106 SEIZMIKA6
0,645
0,23 -0,36
0,01
0,069
0,002 -0,331
STORY2 B106 SEIZMIKA6
1
0,23 -0,21
0,01
0,069 -0,001
-0,23
STORY2 B106 SEIZMIKA7
0 -0,49 -0,45 -0,02 -0,084 -0,004
0,115
STORY2 B106 SEIZMIKA7
0,323 -0,49 -0,31 -0,02 -0,084
0,003
0,238
STORY2 B106 SEIZMIKA7
0,645 -0,49 -0,17 -0,02 -0,084
0,01
0,315
STORY2 B106 SEIZMIKA7
0,645
0,19 -0,45 -0,01
0,071 -0,003 -0,424
STORY2 B106 SEIZMIKA7
1
0,19 -0,29 -0,01
0,071
0,001 -0,293
STORY2 B106 SEIZMIKA8
0
-0,3 -0,46 -0,02 -0,084 -0,003
0,118
STORY2 B106 SEIZMIKA8
0,323
-0,3 -0,31 -0,02 -0,084
0,002
0,243
STORY2 B106 SEIZMIKA8
0,645
-0,3 -0,17 -0,02 -0,084
0,008
0,321
STORY2 B106 SEIZMIKA8
0,645
0,41 -0,46
0
0,069
0,001 -0,435
STORY2 B106 SEIZMIKA8
1
0,41
-0,3
0
0,069
0
-0,3
STORY2 B106 SEIZMIKA9
0 -0,69 -0,31 -0,02
-0,08 -0,004
0,046
STORY2 B106 SEIZMIKA9
0,323 -0,69 -0,17 -0,02
-0,08
0,003
0,122
STORY2 B106 SEIZMIKA9
0,645 -0,69 -0,02 -0,02
-0,08
0,01
0,153
STORY2 B106 SEIZMIKA9
0,645 -0,13 -0,24
0,01
0,069
0,002 -0,202
STORY2 B106 SEIZMIKA9
1 -0,13 -0,09
0,01
0,069 -0,001 -0,143
STORY2 B106 SEIZMIKA10
0 -0,64 -0,31 -0,02
-0,08 -0,004
0,047
STORY2 B106 SEIZMIKA10
0,323 -0,64 -0,17 -0,02
-0,08
0,003
0,124
STORY2 B106 SEIZMIKA10
0,645 -0,64 -0,03 -0,02
-0,08
0,009
0,155
STORY2 B106 SEIZMIKA10
0,645 -0,06 -0,25
0,01
0,069
0,003 -0,205
STORY2 B106 SEIZMIKA10
1 -0,06 -0,09
0,01
0,069 -0,001 -0,145
STORY2 B106 SEIZMIKA11
0 -0,28 -0,53 -0,02 -0,086 -0,004
0,154
STORY2 B106 SEIZMIKA11
0,323 -0,28 -0,39 -0,02 -0,086
0,002
0,303
STORY2 B106 SEIZMIKA11
0,645 -0,28 -0,25 -0,02 -0,086
0,008
0,406
STORY2 B106 SEIZMIKA11
0,645
0,48 -0,56 -0,01
0,07 -0,004 -0,549
STORY2 B106 SEIZMIKA11
1
0,48 -0,41 -0,01
0,07
0,001 -0,377
STORY2 B106 SEIZMIKA12
0 -0,22 -0,53 -0,02 -0,086 -0,003
0,155
STORY2 B106 SEIZMIKA12
0,323 -0,22 -0,39 -0,02 -0,086
0,002
0,304
STORY2 B106 SEIZMIKA12
0,645 -0,22 -0,25 -0,02 -0,086
0,008
0,408
STORY2 B106 SEIZMIKA12
0,645
0,54 -0,57 -0,01
0,07 -0,003 -0,552
STORY2 B106 SEIZMIKA12
1
0,54 -0,41 -0,01
0,07
0,001 -0,379
STORY2 B106 ANVELOPA MAX
0 -0,22 -0,31 -0,02
-0,08 -0,003
0,155
STORY2 B106 ANVELOPA MAX 0,323 -0,22 -0,17 -0,02
-0,08
0,004
0,314
STORY2 B106 ANVELOPA MAX 0,645 -0,22 -0,02 -0,02
-0,08
0,013
0,417
STORY2 B106 ANVELOPA MAX 0,645
0,54 -0,24
0,01
0,109
0,003 -0,202

Završni rad
Ivan
Filipović
61
8.3.1.
Dimenzioniranje na moment savijanja
Za proračun armature su izabrani presjeci i zone koje su mjerodavne prema anvelopi
momentnih dijagrama.
•
Polje
??
????
= 0,555
??????
= 55
????????
Bezdimenzionalni koeficijenti:
??
????
=
??
????
??
??
∙ ??
2
∙ ??
????
=
55
16
∙
27
2
∙
1,667 = 0,003
Za
??
????
= 0,003
očitano:
??
= 0,993
??
??
1
= 20
‰
??
= 0,020
??
??
2
=
−
046
‰
Položaj neutralne osi (udaljenost od tlačnog ruba):
??
=
?? ⋅ ??
= 0,020
⋅
27 = 0,54
????
Potrebna površina armature u polju:
??
??
=
??
????
?? ∙ ?? ∙ ??
????
=
55
0,993
∙
27
∙
34,783 = 0,059
????
2
Minimalna armatura:
??
??
,
??????
= 0,6
∙ ??
??
∙ ?? ∙
1
??
????
= 0,6
∙
16
∙
23
∙
1
400 = 0,552
????
2
Maksimalna armatura:
??
??
,
??????
=
??
??
∙ ?? ∙
0,85
∙ ??
????
??
????
= 16
∙
23
∙
0,85
∙
1,667
34,783 = 14,99
????
2
Odabrana armatura mora se nalaziti u području između minimalne
i maksimalne
armature:
??
??
,
??????
<
??
??
<
??
??
,
??????
ODBRANO:
????????
�??
??
1,
????
= 3,08
????
2
�
Završni rad
Ivan
Filipović
62
•
Lijevi ležaj
??
????
= 0,16
??????
= 16
????????
Bezdimenzionalni koeficijenti:
??
????
=
??
????
??
??
∙ ??
2
∙ ??
????
=
16
16
∙
27
2
∙
1,667 = 0,001
Za
??
????
= 0,001
očitano:
??
= 0,997
??
??
1
= 20
‰
??
= 0,010
??
??
2
=
−
0,2
‰
Položaj neutralne osi (udaljenost od tlačnog ruba):
??
=
?? ⋅ ??
= 0,010
⋅
27 = 0,27
????
Potrebna površina armature :
??
??
=
??
????
?? ∙ ?? ∙ ??
????
=
16
0,997
∙
27
∙
34,783 = 0,02
????
2
Minimalna armatura:
??
??
,
??????
= 0,0015
∙ ??
??
∙ ??
= 0,0015
∙
16
∙
27 = 0,648
????
2
Maksimalna armatura:
??
??
,
??????
= 0,310
∙ ??
??
∙ ?? ∙
??
????
??
????
= 0,310
∙
16
∙
27
∙
1,667
34,783 = 6,41
????
2
Odabrana armatura mora se nalaziti u području između minimalne i maksimalne
armature:
??
??
,
??????
<
??
??
<
??
??
,
??????
ODBRANO:
????????
�??
??
1,
????
= 3,08
????
2
�

Završni rad
Ivan
Filipović
64
8.3.2.
Dimenzioniranje na poprečne sile
??
????
= 0,61
????
Proračunska nosivost na oprečnu silu elementa bez poprečne armature:
??
????
1
= {
??
????
∙ ?? ∙
(1,2 + 40
??
1
) + 0,15
??
????
}
∙ ??
??
∙ ??
gdje je:
??
????
= 0,034
????
/
????
2
osnovna računska čvrstoća
??
= 1,6
− ??
= 1,6
−
0,23 = 1,37
pretpostavka:
2
Φ
14
�??
??
1,
????
= 3,08
????
2
�
prelaze preko ležaja,
??
1
=
??
??
??
??
∙??
=
3,08
16
∙
23
= 0,008
??
????
= 0,0
????
/
????
2
??
????
1
= {0,034
∙
1,37
∙
(1,2 + 40
∙
0,008) + 0,15
∙
0}
∙
16
∙
23 = 26,05
????
??
????
<
??
????
1
0,61 < 26,05
????
nije potreban je proračun poprečne armature
•
Minimalna poprečna armatura (maksimalni razmak odabranih vilica):
Odabrano:
??
????
,
??????
= (2
??????????
Φ
8 ) = 1,01
????
2
Treba proračunati najveći razmak po oba kriterija (uvjeta) i odabrati manji.
1.
Uvjet
??
????
,
??????
=
??
??????
∙ ??
??
∙ ??
??
Gdje je:
??
??
,
??????
-
minimalni koeficijent armiranja poprečne armature ovisno o kakvoći betona i
čelika
??
??
,
??????
= 0,0009
koef. Armiranja za beton klase C
25/30 i čelik RA 400/500
??
??
,
??????
=
??
????
,
??????
??
??????
∙ ??
??
=
1,01
0,0009
∙
16 = 70,14
????
Završni rad
Ivan
Filipović
65
2.
Uvjet
??
????
2
= 0,5
∙ ?? ∙ ??
????
∙ ??
??
∙ ??
Gdje je:
??
-
koeficijent redukcije tlačne čvrstoće betonskih tlačnih štapova
??
= 0,7
−
??
????
200 = 0,575
??
??
- najmanja š
irina presjeka u vlačnoj zoni, 16
cm
??
= 0,9
∙ ??
= 0,9
∙
23 = 20,7
????
krak unutarnjih sila
??
????
= 1,667
????
/
????
2
računska čvrstoća na tlak
??
????
2
= 0,5
∙
0,575
∙
1,667
∙
16
∙
20,7 = 158,73
????
Ako je:
??
????
<
1
5
??
????
2,78 < 31,75
??
??
,
??????
= 0,8
∙ ??
= 0,8
∙
23 = 18,4
????
< 30
????
??
??
,
??????
= 18
????
Mjerodavan najveći razmak od
abranih vilica
Φ
8
, m=2:
??
??
,
??????
= 18
????
(iz drugog
uvjeta). Odabrani razmak mora biti manji od s
w,max
ODBRANO:
????
/
????
,
??
=
??
8.4.
Plan armature stupa i grede

Završni rad
Ivan Filipović
68
9.
Komentar provedene analize

Završni rad
Ivan Filipović
70
Slika 9.0. Presjek 1
-1
Slika 9.1. Presjek 5
-
5
Slika 9.2. Presjek A
-A
Završni rad
Ivan Filipović
71
Slika 9.3. Presjek B
-
B
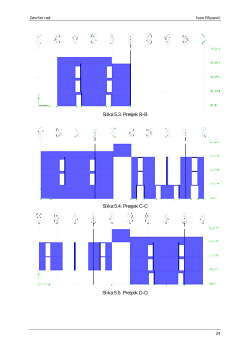
Slika
9s
.4. Presjek C
-
C
Slika 9.5. Presjek D
-
D

Završni rad
Ivan Filipović
73
10.
Literatura
Završni rad
Ivan Filipović
74
[1] Eurocode 1: Osnove projektiranja i djelovanja na konstrukcije,
Hrvatski zavod za normizaciju i mjeriteljstvo, prvo izdanje, listopad 2005.
[2] Eurocode 2: Projektiranje betonskih konstrukcija,
Hrvatski zavod za normizaciju i mjeriteljstvo, prvo izdanje, prosinac 2005.
[3] Eurocode 8: Projektiranje konstrukcija otpornih na potres,
Hrvatski zavod za normizaciju i mjeriteljstvo, prvo izdanje, veljaca 2005.
[4] I. Tomi
čić
: Betonske konstrukcije,
Društvo hrvatskih gra
đ
evinskih konstruktora, Zagreb, 1996.
[5] J. Radi
ć
i suradnici: Betonske konstrukcije, priru
č
nik,
SECON HDGK d.o.o, Zagreb, 2006.
Želiš da pročitaš svih 1 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































