Napomena: Neke opcije za prijavu su dostupne samo nakon kupovine dokumenta.
1
RАVANSKE REŠETKE
Rešetkasti nosa
č
i predstavljaju sistem sa
č
injen od lakih krutih štapova me
đ
u-
sobno zglobno vezanih svojim krajevima. Zglobne veze krajeva štapova se nazivaju
č
vorovi. Rešetke su optere
ć
ene koncentrisanim silama koje leže u ravni rešetke i
dejstvuju u njenim
č
vorovima.
Osnovni element svake ravanske rešetkaste kontrukcije je trougao. Izme
đ
u broja
č
vorova
n
i broja štapova
s
stati
č
ki odre
đ
ene ravanske rešetke postoji veza
s
=2
n
-3.
Ukoliko je
s
>2
n
-3 postoji
unutrašnja
stati
č
ka neodre
đ
enost
rešetke
, a ako je
s
<2
n
-3
radi se o mehanizmu
Rešetka može biti vezana za podlogu pokretnim zglobom, nepokretnim zglo-
bom, užetom ili lakim štapom. Laki štap koji povezuje rešetku sa osloncima nije
sastavni deo ravanske rešetke, ve
ć
njena spoljašnja veza.
Prora
č
un rešetke se svodi na odre
đ
ivanje reakcija spoljašnjih veza i sila u šta-
povima rešetke. Zbog uvedenih pretpostavki sile u lakim štapovima se poklapaju s
pravcima lakih štapova, te oni mogu biti optere
ć
eni na zatezanje ili pritisak.
1.1
Algoritam rešavanja zadataka
Prora
č
un rešetke se može izvršiti na osnovu slede
ć
ih koraka:
1. Osloboditi se spoljašnjih veza i uvesti odgovaraju
ć
e reakcije veza (otpore
oslonaca).
2. Za rešetku kao celinu pisati jedna
č
ine ravnoteže i odrediti reakcije veza.
Naime, kako na rešetku dejstvuje ravanski sistem sila njena ravnoteža
ć
e biti ostva-
rena ako su glavni vektor sistema i glavni moment
za proizvoljno izabranu tačku A
jednaki nuli:
F
M
g
g
=
=
0
0
,
.
A
(1.1)
Prvi, vektorski uslov se projektovanjem na ose koordinatnog sistema
xy
svodi na
dve skalarne jedna
č
ine, a prethodni uslovi ravnoteže transformišu u slede
ć
i sistem
jedna
č
ina ravnoteže
1
:
1
0 3
0
1
1
.
,
0
.
,
0
∑
∑
0 2
,
0
.
∑
=
1
+
i
n
i
n
yi
0 2
,
00 2
(1.2)
1
U daljem tekstu
ć
e se tokom rešavanja primera izostavljati oznaka za promenu indeksa
i
=1,...,
n
sume projekcija svih
sila, ali
ć
e se podrazumevati da se ta suma odnosi na sve sile koje dejstvuju na uo
č
eni sistem. Indeks sumiranja
ć
e
i u momentnim jedna
č
inama, pri rešavanju primera, biti izostavljan. Na taj na
č
in, oznaka
M
A
+
∑
ć
e podrazumevati
∑
∑
=
=
+
j
k
j
i
n
F
i
1
1
M
M
A
(sumu spegova i momenata sila za izabranu ta
č
ku) za nazna
č
en pozitivan smer momenta.
RAVANSKE REŠETKE
8
koji podrazumeva da je suma projekcija svih sila na ose koordinatnog sistema jednaka nuli, i da je suma momenata svih sila i spregova za proizvoljnu ta
č
ku u ravni nula.
Osim jedna
č
ina ravnoteže (1.2), mogu se pisati i alternativni oblici jedna
č
ina
ravnoteže ([1], str. 52). Jedan od njih se ogleda u pisanju tri momentne jedna
č
ine
za
ta
č
ke A, B i C:
1
0 3
0
.
,
0
.
,
0
∑
∑
0 2
,
∑
+
+
+
0 2
0 22
,
0
.
0 2
,
00 2
(1.3)
pri
č
emu su A, B i C nekolinearne ta
č
ke.
3. Nakon odre
đ
ivanja otpora oslonaca, vrši se izra
č
unavanje sila u šta-
povima, što se može izvršiti na dva na
č
ina: metodom izdvajanja
č
vorova i
metodom izdvajanja dela rešetke (metod preseka, Riterov metod).
Ukoliko se primenjuje
metod izdvajanja
č
vorova
, polazi se od
č
vora u
kome se su
č
eljavaju samo dva štapa. Sile u lakim štapovima, kao unutrašnje
sile, pretpostavljaju se kao zatezne. Osim toga, sile reakcije veze istog lakog štapa koje dejstvuju na razli
č
ite
č
vorove se postavljaju po principu akcije i
reakcije. Pisanjem jedna
č
ina ravnoteže za su
č
eljan sistem sila u ravni:
1
0
2
0
1
1
.
,
.
.
∑
∑
=
=
=
=
i
n
xi
i
n
yi
F
F
(1.4)
odre
đ
uju se sile u štapovima. Sukcesivno, prelazi se sa
č
vora na
č
vor, ima-
ju
ć
i u vidu da broj nepoznatih sila koje dejstvuju u
čvoru
bude najviše dva.
Dobijeni predznak minus uz intenzitet sile u lakom štapu ukazuje da je taj štap pritisnut, dok predznak plus ukazuje da je štap zategnut.
Pri primeni
metoda izdvajanja dela rešetke
vrši se zamišljeno prese-
canje rešetke po štapovima u kojima je potrebno odrediti sile, tako da broj prese
č
enih štapova ne bude ve
ć
i od tri. Zatim se zamenjuje uticaj prese
č
enih
štapova silama koje su im kolinearne i zatezne. Pošto je rešetka na ovaj na-
č
in podeljena na dva dela, a svaki od njih mora biti u ravnoteži, bira se deo
rešetke za koji
ć
e se pisati jedna
č
ine ravnoteže. Preporu
č
ljivo je posmatrati
onaj deo rešetke na koji dejstvuje manje sila. Tako
đ
e, preporu
č
uje se pisa-
nje tri momentne jedna
č
ine za tri nekolinearne ta
č
ke (1.3), iako je mogu
ć
e
pisati i druge oblike jedna
č
ina ravnoteže, na pr. (1.2).
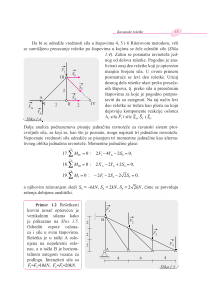
Slika 1.2
RAVANSKE REŠETKE
10
od
č
vora A (numerisanog rimskim I). U ovom
č
voru dejstvuju komponente reakcije
nepokretnog zgloba
X
Y
A
A
i
i sile u štapovima 1 i 2 nepoznatih intenziteta i smerova,
u pravcu štapova. Pogodno je pretpostaviti da su štapovi optere
ć
eni na zatezanje,
a
priori
. To zna
č
i da pri analizi ravnoteže
č
vora smer sila u štapovima ide od posma-
tranog
č
vora ka štapu. Na slede
ć
im slikama prikazani su sistemi sila koji dejstvuju na
č
vorove, a pored slike su ispisane jedna
č
ine ravnoteže
3
:
Č
vor I:
4
0
0
5
0
0
1
2
2
2
2
2
2
.
:
,
.
:
.
F
X
S
S
F
Y
S
xi
yi
∑
∑
=
+ +
=
=
+
=
A
A
Rešavanjem ovih jedna
č
ina dobija se da su sile u štapovima
S
kN S
kN
1
2
2
4 2
=
= −
, ,
odakle se zaklju
č
uje da je štap 1 zategnut, jer je dobijena vrednost za silu u štapu 1
pozitivna. S obzirom da je predznak ispred vrednosti sile u štapu 2 negativan, sledi da je štap 2 optere
ć
en na pritisak.
Sada se prelazi na
č
vor II, u kome su vezani štapovi 1, 3 i 4. Nepoznate u jedna-
č
inama ravnoteže za ovaj
č
vor bi
ć
e sile u štapovima 3 i 4, dok je zbog principa akcije
i reakcije sila u štapu 1 poznatog intenziteta
4
.
3
Kako u ovom primeru svi kosi štapovi rešetke zaklapaju sa horizontalnim i vertikalnim pravcem uglove od 45°,
vrednosti tih uglova ne
ć
e biti posebno nazna
č
eni na slikama.
4
Pri reš
а
v
а
nju primer
а
vektori svih sila
ć
e se postavlj
а
ti jedan u odnosu na drugi po principu akcije i reakcije,
t
е
obeležavati istom slovnom oznakom uz dodatak oznake prim ’ (na pr.
S
S
1
i
1
’
), pri
č
emu
ć
e se u jedna
č
inama uvek
koristiti jednakost intenziteta tih sila ozna
č
eno bez prima (
S
S
1
=
1
’
).
B
A
R
2
2
2
R
2
F
1
F
2
F
3
F
4
Y
A
X
A
Y
B
y
x
I
II
III
IV
V
VI
VII
VIII
1
2
3
4
5
6
7
8
9
10
11
13
12
2
2
A
Y
A
X
A
I
S
1
S
2
Ravanske rešetke
11
Č
vor II:
6
0
0
7
0
0
1
4
3
.
:
,
.
:
.
F
S
S
F
S
xi
yi
∑
∑
=
− +
=
=
=
Odavde sledi da je štap 3 neoptere
ć
en, a sila u štapu 4 je
S
kN
4
2
=
, što zna
č
i da je
ovaj štap zategnut.
Č
vor III:
8
0
0
9
0
0
2
2
2
5
2
2
6
2
2
2
5
2
2
3
1
.
:
,
.
:
.
F
S
S
S
F
S
S
S
F
xi
yi
∑
∑
=
−
+
+
=
=
−
−
− − =
Na osnovu napisanih jedna
č
ina je
S
kN S
kN
6
5
6
2 2
= −
=
,
.
Analogno ovoj proceduri izvrši
ć
e se analiza ravnoteže preostalih
č
vorova.
Č
vor IV:
10
0
0
11
0
0
4
5
2
2
8
2
2
5
2
2
7
8
2
2
.
:
,
.
:
.
F
S
S
S
F
S
S
S
xi
yi
∑
∑
=
−
−
+
=
=
+
+
=
Dakle, intenzitet sile u štapu 8 je
S
kN
S
kN
8
7
4 2
6
=
= −
,
.
dok je
Č
vor V:
12
0
0
13
0
0
10
2
2
9
6
2
7
10
2
2
.
:
,
.
:
.
F
S
S
S
F
F
S
S
xi
yi
∑
∑
=
+
−
=
=
−
− +
=
Intenziteti sila u štapu 9 i 10 su
S
kN S
kN
9
10
2
4 2
= −
= −
, .
Č
vor VII:
14
0
0
15
0
0
10
2
2
13
2
2
4
10
2
2
13
2
2
11
.
:
,
.
:
.
F
S
S
F
F
S
S
S
xi
yi
∑
∑
=
−
+
−
=
=
−
−
−
=
II
S
1
S
3
S
4
,
F
1
III
S
5
S
3
S
2
S
6
,
,
IV
S
4
S
5
S
8
,
,
S
7
F
2
V
S
7
S
9
S
10
S
6
,
,
F
4
VII
S
10
S
11
S
13
,
Slika 1.4
Slika 1.5
Ravanske rešetke
13
Da bi se odredile vrednosti sila u štapovima 4, 5 i 6 Riterovom metodom, vrši
se zamišljeno presecanje rešetke po štapovima u kojima se žele odrediti sile (
Slika
1.4
). Zatim se posmatra ravnoteža jed-
nog od delova rešetke. Pogodno je ana- lizirati onaj deo rešetke koji je optere
ć
en
manjim brojem sila. U ovom primeru posmatra
ć
e se levi deo rešetke. Uticaj
desnog dela rešetke ulazi preko prese
č
e-
nih štapova, tj. preko sila u prese
č
enim
štapovima za koje je pogodno pretpos- taviti da su zategnuti. Na taj na
č
in levi
deo rešetke se tretira kao plo
č
a na koju
dejstvuju komponente reakcije oslonca A, sila
F
1
i sile
S S
S
4
5
6
,
i .
Dalja analiza podrazumeva pisanje jedna
č
ina ravnoteže za ravanski sistem proi-
zvoljnih sila, za koji se, kao što je poznato, mogu napisati tri jedna
č
ine ravnoteže.
Nepoznate vrednosti sila odredi
ć
e se pisanjem tri momentne jedna
č
ine kao alterna-
tivnog oblika jedna
č
ina ravnoteže. Momentne jedna
č
ine glase:
17
0
2
4
2
0
18
0
2
2
2
0
19
1
6
4
.
:
,
.
:
,
.
∑ ∑ ∑
+
+
=
−
−
=
=
−
+
=
M
F
Y
S
M
X
Y
S
IV
A
III
A
A
++
=
−
−
−
=
M
F
S
S
I
0
2
2
2 2
0
1
6
5
:
,
a njihovim rešavanjem sledi
S
kN S
kN S
kN
6
4
5
6
2
2 2
= −
=
=
, ,
,
č
ime se potvr
đ
uju
rešenja dobijena analiti
č
ki.
Primer 1.2
Rešetkasti
krovni nosa
č
optere
ć
en je
vertikalnim silama kako je prikazano na
Slici 1.5
.
Odrediti otpore oslona- ca i sile u svim štapovima. Rešetka je u ta
č
ki A oslo-
njena na nepokretni oslo- nac, a u ta
č
ki B je horizon-
talnom zategom vezana za podlogu. Intenziteti sila su
