Gimnazija u Pirotu
jun,2006
Maturski rad iz matematike
Skalarni proizvod
vektora
1
Mentor:
ucenik:
prof.Valemtina Kostic
Ivan Jovanovic
IV
5
Pojam vektora
-Definicija.Velicine odredjene svojom brojnom
vrednoscu,pravcem i smerom zovu se
vektorske velicine
ili
vektori.
-Neke vaznije osobine vektora:
1.Pomeranje,sila,brzina,ubrzanje,moment sile,jacina
magnetnog polja,i dr.-primeri su velicina koje su odredjene
svojom brojnom vrednoscu,pravcem i smerom.
2.Dva vektora su jednaka ako su istog pravca i istog smera i
imaju jednake brojne vrednosti u odnosu na istu jedinicu.
3.Duzina ili intenzitet vektora zove se jos i apsolutna
vrednost ili modul,na primer za vektor
,
oznacavamo
.
4.Vektor je takodje okarakterisan uredjenim parom
tacaka,pa se zato i tako oznacacava,npr. (A,B) , (M,N) , itd.
5.Sve vektore koje leze na istoj pravoj nazivamo
kolinearnim vektorima.
6.Vektor duzine 1 zove
se jedinicni vektor
ili
ort
2
A kako su algebarske vrednostitih vektora na osi LL’
(4) AB=
, CD=
,
imacemo
=AB ,
=CD .
Osa na kojoj su utvrdjene tacke
0 i 1
zove se,kao sto je
poznato,koordinatna osa;tacku 0 – koordinatni pocetak –
oznacavamo sa 0,a koordinatnu osu sa ,
i sl.Koordinatna
osa je , preme tome,odredjena svojim jedinicnim vektorom
i zadaje se tim vektorom.Izmedju skupa
realnih brojeva i skupa svih tacaka na koordinatnoj
osi(brojevnoj pravoj), postojiuzajamno jednoznacna
korespondencija:svakoj tacki odgovara po jedan realan broj i
svakom realnom broju odgovara po jedna tacka na koordinatnoj
pravoj.
Ako su
i
ma koja dva vektora na osi
tada
uvek mozemo naci takav broj
da je
,
To jest
.
Za vektore
i
tada kazemo da su
linearno zavisni.
Dva vektora istog pravca (bez obzira da li su na istoj pravoj
ili na paralelnim pravim) nazivamo
kolinearnim
( u sirem
smislu );ako dva vektora nemaju isti pravac ,nazivamo ih
nekolinearnim
vektorima;ocigledno,ti vektori nisu linearno
zavisni.
4
y
y
Sl.1.2
sl.1.3
Uocimo sada u ravni,dva uzajamno ortogonalna jedinicna
vektora,
i , sa zajednickim pocetkom 0 (sl.1.2).ti vektori
odredjuju dve uzajamno ortogonalne koordinatne ose , i
,sa zajednickim koordinatnim
pocetkom 0.Svaki vektor
(tj.
vektor polozaja svake tacke
)u toj ravni mozemo predstaviti kao zbir jednog vektora
na osi
i
jednog na osi
(tj. razloziti u komponente duz vektora
i
)
;dobicemo:
(5)
, (sl.1.3)
gde je
(6)
,
(sa
i oznacene su,redom,algebarske vrednosti
i
vektora
,odn.
).Sada , na osnovu (6) mozemo OA
predstaviti zbirom
(7)
,
5
1
x
1
0
x
A
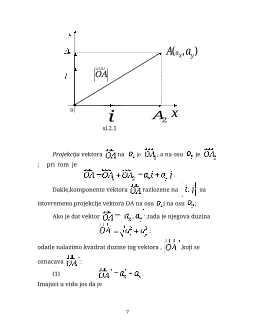
sl.2.1
Projekcija
vektora
na
je
, a na osu
je
; pri tom je
.
Dakle,komponente vektora
razlozene na
su
istovremeno
projekcije vektora OA na osu
i na osu ;
Ako je dat vektor
,tada je njegova duzina
;
odatle nalazimo kvadrat duzine tog vektora ,
,
koji se
oznacava
:
(1)
.
Imajuci u vidu jos da je
i
2
A
x
0
OA
( , )
ax y
A a
7
