
Statička i dinamička karakteristika signala Pregled
STATIČKA I DINAMIČKA KARAKTERISTIKA SIGNALA
STATIC AND DYNAMIC CHARACTERISTICS OF SIGNALS
Amir Hajdarević
Mašinski fakultet
Ključne riječi:
mjerenje, signal, Fourier-ov niz
SAŽETAK:
Mjerenje je određivanje vrijednosti fizikalne veličine skupom eksperimentalnih operacija uz pomoć
odgovarajućih tehničkih sredstava mjerenja. Moderna mjerenja baziraju se uglavnom na pretvaranju fizikalnih
veličina u električni signal. Signali mogu biti klasificirani kao analogni ili digitalni. Kroz ovaj rad su dati
Fourier-ovi nizovi i koeficijenti te primjeri određivanja istih za zadane funkcije.
Keywords:
measurement, signal, Fourier series
ABSTRACT:
Measurement is defining value of psyhical quantity of experimental operation with help of technical
measurement elements. Modern measurement are based on transforming psychical quantity in to electric signal.
Signals can be clasified like analog and digital. In this seminar work we put Fouriers series and koeficients, and
some exampls of defining this series for particural function.
1. UVOD
Sistem za mjerenje pretvara ulaznu vrijednost u izlazne veličine koje se mogu promatrati i snimiti, kao
što je npr. kretanje pokazivača ili magnituda na digitalnom zaslonu. Krajnji cilj svakog mjernog
sistema je dati tačne podatke o vrijednosti na ulazu, koji su mjerena veličina. Mi koristimo izlaz
mjernog sistema za dobivanje informacija o ulaznoj varijabli. Sistem mjeri tačne vrijednosti određene
ulazne varijable, a oblik ili karakteristike ulazne količine utiču na greške u mjerenju. No, kvaliteta
informacija koje nastaju iz mjerenja ovisi o pravilnom izboru sistema mjerenja i pravilnog tumačenje
rezultata mjerenja. Razumijevanje prirode i oblik ulaznog signala u sistem mjerenja su važni za izbor
mjernog sistema za određeni zadatak. Naš cilj je da razumijemo osobine ulaznih signala u sistem
mjerenja i rezultat mjerenja signala. Informacije o veličini, prije svega misli se na ulaznu veličinu i
učestalosti frekvencije pokazuje način na koji se signal mjenja u vremenu, a taj način potreban je za
procjenu mjernih sistema. Oblici signala često se nazivaju valni oblici.
2. ULAZNO / IZLAZNI KONCEPTI SIGNALA
Dva važna zadatka koje inžinjeri susreću u mjerenju fizičke varijable su:
l. Odabir mjernog sistema, i
2. Ocjenjivanje izlaza iz sistema mjerenja.
Jednostavan primjer odabira mjernog sistema može biti izbor sistema za mjerenje zraka u gumama od
bicikla ili u auto gumama. Mjerač za auto gume mora biti u mogućnosti mjeriti pritiske do 40 lb/in
2
,
dok mjerač guma za bicikl mora ukazati znatno veće pritiske, možda i do 100 lb/ in
2
. Ova ideja o
rasponu na instrumentima je osnovna na svim mjernim sistemima, i pokazuje da se neke osnovne
naravi ulaznog signala, u ovom slučaju veličina, moraju procjeniti i izvršiti odabir mjernog sistema za
određenu primjenu.
Amir Hajdarević – Statička i dinamička karakteristika signala
Mašinski fakultet Mostar, maj 2013.
2
Puno teži zadatak je procjena izlazih veličina sistema mjerenja kada ponašanje ulaznog signala nije
poznato. Tlak u gumi se ne mijenja dok mi pokušavamo da ga mjerimo, ali šta ako mi na neki način
povežemo mjerač guma na cilindar automobilskog motora? Mi znamo da je pritisak u cilindru različit,
odnosno da varira s vremenom. Ako je naš zadatak bio odabrati sistem mjerenja kako bi se utvrdio
vremenski promjenjivi pritisak, moramo poznavati informacije o pritisku u cilindru koji varira. Iz
termodinamike i pomoću raspona brzine motora možemo odrediti raspon pritisaka koji se očekuju, kao
i brzinu kojom se pritisak mijenja. Mnogi sistemi mjerenja pokazuju slične odgovore pod raznim
uvjetima, što sugerira da se performanse i sposobnosti mjernog sistema mogu opisati na generalizirani
način. Riječ generalizirati podrazumijeva da se odnos između ulaznih i izlaznih veličina za razne
mjerne sisteme može opisati pomoću zajedničkih varijabli. Da bi ispitali dodatno generalizirano
ponašanje sistema mjerenja, prvo moramo ispitati moguće oblike ulaznih i izlaznih signala. Izraz
signal se koriste u kombinaciji s prijenosom podataka. On se koristi za opisivanje fizičke varijable,
koja je funkcija vremena, i zadatak mu je da komunicira sa sistemom mjerenja, bilo kao ulaz u mjerni
sistem ili kao izlaz iz mjernog sistema. Dakle, signal je podatak o izmjerenoj varijabli koji se prenose
između procesa i mjernog sistema, ili između faza mjernog sistema.
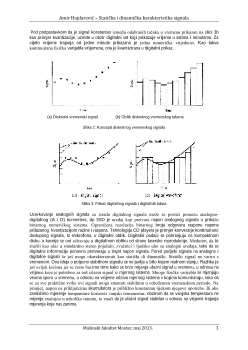
2.1. Oblici signala
Signali mogu biti klasificirani kao analogni ili digitalni. Analogni opisuje signal koji je kontinuiran u
vremenu. Očito da fizičke varijable imaju tendenciju da se stalno ponavljaju u prirodi, analogni signal
predstavljanja njegovu zavisnost od vremenskog ponašanja. Pored toga, magnituda signala je
kontinuirana i na taj način može imati bilo koju vrijednost unutar radnog raspona. Analogni signal je
prikazan na slici 1a, slično njemu kontinuirani signal snimanja je prikazan na pokazivaču, slika 1b.
Kontrast ovog kontinuiranog signala je prikazan na slici 2a. Ovaj oblik predstavlja diskretni vremenski
signal, gdje su informacije o magnitudi signala dostupne samo na diskretnim točkama u vremenu.
Diskretni signal obično rezultira uzorkovanjem kontinuiranih varijabli na konačnim vremenskim
intervalima.
(a) Prikaz analognog signala (b) Analogni displej
Slika 1: Analogni pojmovi vezani za signal
Informacije o signalu prikazanom na
slici 2a
, su dostupne samo diskretnim putem. Općenito, veličina
uzorkovanja mora biti dovoljno visoka da se signal može pretpostaviti kao konstantan tijekom
vremena. Signal koji proizlazi iz ove pretpostavke prikazan je na
slici 2b
. Jasno, ukoliko je vrijeme
između mjerenja smanjeno, tako se i diskretna varijabla kao i kontinuirani signal predstavljanja
smanjuju. Digitalni signali su osobito korisni kada se vrši prikupljanje i obrada podataka, koji se
izvode pomoću digitalnog računala. Digitalni signal ima dvije važne karakteristike. Prvo, digitalni
signal ima diskretne vrijednosti u vremenu, kao i diskretnom vremenskom signalu, a magnitudom
digitalnog signala određuje se proces poznat kao kvantizacije, u trenutku vremena. Kvantizacijski
jedan broj predstavlja niz veličina kontinuiranog signala ili variabli.
Slika 3a
prikazuje oblike digitalne
i analogne forme istog signala, gdje veličine u digitalnim signalima mogu imati samo određene
diskretne vrijednosti. Dakle, digitalni signal pruža kvantizirane magnitude u diskretnom vremena.
Amir Hajdarević – Statička i dinamička karakteristika signala
Mašinski fakultet Mostar, maj 2013.
4
S druge strane, mjerni sistemi su često potrebni kako bi se utvrdilo mjerenje varijable koja je
predstavljena kao promjenjiva funkciji. Drugim riječima, izlazni sistemi mjerenja moraju pratiti način
promjene ulaznog signala.
Tabela 1. Klasifikacija talasa
I. Statički
y(t)
= Ao
II. Dinamički
Jednostavni periodični talasi:
y(t)
= Ao + C sin( ωt + ϕ )
Složeni periodični talasi:
∑
Neperiodični talasi
Korak:
y(t)
= AoU(t) = Ao za t > 0
RAMP:
y(t)
= Kt za 0 < t < t
f
PULSE:
y(t)
= AoU(t) - AoU( t – t
1
)
III. Nedeterministični talasi
∑
U(t) predstavlja funkciju, koja je nula za t < 0 i t ≥ 0.
Dinamički signal je definisan kao vremenski signala. Općenito, oblik dinamičkih talasa y(t), može biti
klasificiran kao što je prikazano na
slici 4
. Deterministički signal je onaj signal koji varira u vremenu,
na određen način, kao što su talasi sinusoide. Signal je periodičan ako se varijacija magnitude signala
ponavlja u pravilnom obliku u vremenskim intervalima. Primjer periodičnog ponašanja je promjena
temperature u cilindru SUS motora, pod stalnim radnim uslovima. Periodični talasi se mogu podijeliti
na jednostavne ili složene, složeni periodični talas sadrži više frekvencija. Neperiodični se koristi za
opisivanje determinističkog signala koji se ne ponavlja u određenim vremenskim razmacima, kao što
je korak funkcije. Također na slici 4 opisan je nedeterminističan signal koji nema mogućnost
ponavljanja. Nedeterministični signal ne može biti propisan prije nego se dogodi, iako se određene
karakteristike signala mogu biti poznate unapred. Kao primjer, zamislite prijenos podataka sa jednog
na drugi računar. Karakteristike signala poput broja prijenosa podataka i mogući raspon signala
prikazan na magnitudi je poznat za bilo koji signal u tom sistemu. No, to ne bi bilo moguće predvidjeti
ubuduće za karakteristike signala bazirane na temelju postojećih informacija u tom signalu. Takav
signal se s pravom naziva nedeterminističan.
Amir Hajdarević – Statička i dinamička karakteristika signala
Mašinski fakultet Mostar, maj 2013.
5
Slika 4: Primjer dinamičkog signala
Ključni faktor u sistemu mjerenja bazira se na prirodi ulaza u sistem. Određena sredstva su potrebna
za klasifikaciju valnih oblika za ulazni signal, a i kao rezultat izlaznih signala u odnosu na njihove
veličine i učestalosti. To bi bilo vrlo korisno kada bi se sistem mjerenja mogao definisati u zavisnosti
od vrste ulaznih signala. Ovo je upravo slučaj kada imamo sljedeće: vrlo kompleksni signali, čak i oni
koji su nedeterministični u prirodi, mogu se približiti kao beskonačni niz sinus i kosinus funkcije, što
je prikazano u tabeli 1. Način izražavanja tako složenog signala kao niza sinusne i kosinusne funkcije
se zove
Fourierova analiza
. Na primjer, bogati glazbeni tonovi mogu biti generirani kombiniranjem
više različitih čistih tonova. Fourierove analize odlićno predstavljaju fizičku analogiju koja se
prikazuje kao prizma. Slika 5 ilustrira preobrazbu složenog vala, predstavljenog kao
''white light''
u
neke jednostavnije komponente predstavljene kao
''spectrum''
. U ovom primjeru, boje u spektru su
predstavljene kao jednostavna periodična funkcija koja je prikazana u obliku
''white light''
. Fourierova
analiza je otprilike ekvivalent matematičkoj prizmi, i daje prikaz složenog signala u smislu
jednostavnih periodičnih funkcija.
Slika 5: Razdvajanje bjele svijetlosti u svom spektru boja
Prikaz složenih signala u obliku jednostavnih periodičnih funkcija omogućuje sistemu mjerenja da
relativno dobro definiše izlaz koji proizilazi iz nekoliko određenih ulaznih signala, od kojih jedna
mora biti jednostavna periodična.
3. FOURIER-OVA ANALIZA
Cilj ovog članka je razviti osnovno razumijevanje o frekvenciji i amplitudi oba, i determinističkog i
nedeterminističkog signala. Jednostavan, periodični talas definitivno ima jednu dobro definisanu
amplitudu i frekvenciju. S druge strane, nedeterministički signali imaju više komponenti frekvencije i
različite amplitude, i zahtijevaju određenu analizu kako bi se utvrdila njihova frekvencija. Temeljni
pojmovi vezani za frekvenciju i amplitudu proizilaze iz analize periodičnih pokreta. Iako se funkcije
sinusa i kosinusa prema geometrijskoj definiciji odnose na dužine strane pravougaonog trokuta, za
naše potrebe sinus i kosinus je najbolje posmatrati kao matematičku funkciju koja opisuje određena
fizička ponašanja sistema. Ta ponašanja su opisana pomoću diferencijalnih jednačina koje imaju sinus
i kosinusa kao svoja rješenja.
Želiš da pročitaš svih 15 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































