1
Sveučilište u Zagrebu
Edukacijsko-rehabilitacijski fakultet
Znanstveno-učilišni kampus
Borongajska cesta 83f, Zagreb
STATISTIKA
(zadaci za vježbe)
Priredio
Prof.dr.sc. Branko Nikolić
Akademska godina:
2013./2014.
2
1. Vježbe za 1. kolokvij
VJEROJATNOST
1. Za evaluaciju rehabilitacijskog programa koji će se tijekom 6 mjeseci provoditi u Centru za
odgoj i obrazovanje Prekrižje iz Zagreba, potrebno je odabrati jednog učenika. Vjerojatnost
odabira učenika iz razrednog odjeljenja A iznosi p1=0,15, vjerojatnost odabira učenika iz
razrednog odjeljenja B iznosi p2=0,25 dok je vjerojatnost odabira učenika iz odjeljenja C
p3=0,45. Kolika je vjerojatnost da za rehabilitacijski program neće biti odabran učenik iz
odjeljenja A, B i C već iz odjeljenja D?
Rješenje:
p1=0,15
p2=0,25
p3=0,4
Odgovor:
Vjerojatnost da će za provođenje rehabilitacijskog programa biti odabran učenik iz razrednog
odjeljenja D iznosi 0,15.
2. U Centru za odgoj i obrazovanje Prekrižje iz Zagreba imaju dva odjeljenja 6. razreda. U
odjeljenju A ima ukupno 15 učenika s teškoćama, a u odjeljenju B ima ukupno 5 učenika s
teškoćama. Za provođenje rehabilitacijskog programa potrebno je formirati uzorak od 5
učenika šestog razreda. Kolika je vjerojatnost da će svih 5 odabranih učenika biti iz odjeljenja
A?
Rješenje:
n=20
r=15
s=5
4
KOMBINATORIKA
PERMUTACIJE BEZ PONAVLJANJA:
4. Na koliko različitih načina može za stolom sjediti 4 djece s oštećenjem vida na 4 stolice?
Napisati sve moguće razmještaje.
Rješenje:
n=4
Odgovor:
Četiri osobe s oštećenjem vida mogu za stolom sjediti na 24 različita načina.
PERMUTACIJE S PONAVLJANJEM
5. Na koliko različitih načina možemo poredati 2 bijela i 3 bijelo-crvena štapa za slijepe i
gluho-slijepe osobe? Napisati sve permutacije ako su oznake: b-bijeli štab, c-bijelo-crveni.
Rješenje:
n=5
s=2
r=3
5
KOMBINACIJE BAZ PONAVLJANJA:
6. Djeca s invaliditetom koja ljetuju na moru došla su na ručak u jedan restoran. Na koliko se
različitih načina može tih 48 djece s invaliditetom smjestiti za stolove po četvero?
Rješenje:
n=48
r=4
Odgovor:
Na 194 580 različitih načina moguće je smjestiti 48 djece s invaliditetom za stolove po
četvero.
KOMBINACIJE S PONAVLJANJEM:
7. Neka se u bubnju nalazi 10 kuglica. Koliko kombinacija od 3 kuglice možemo formirati
ako je dozvoljeno izvučenu kuglicu vratiti natrag u bubanj?
Rješenje:
n=10
r=3
Odgovor:
Možemo formirati 220 kombinacija od 3 kuglice.
VARIJACIJE BEZ PONAVLJANJA
8. U grupi se nalaze 4 osobe s invaliditetom. Koliko je moguće formirati parova osoba s
invaliditetom vodeći računa o poretku tih osoba.
Rješenje:
n=4
r=2
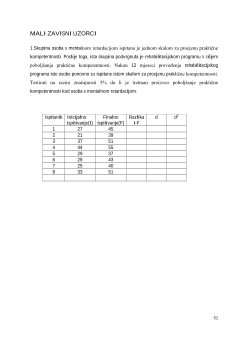
7
MJERE CENTRALNE TENDENCIJE
1. Na varijabli Školska kompetencija (ŠKOKOM) 32 djece s teškoćama postiglo je slijedeće
rezultate:
9,13,19,12,19,17,14,12,13,7,17,7,14,15,8,11,17,16,18,16,13,9,15,9,19,20,22,20,11,6,12,19
a)
Izračunati aritmetičku sredinu, medijan i mod
b)
Distribuirati rezultate u 6 razreda te izračunati relativne frekvencije,
kumulativne frekvencije, relativne kumulativne frekvencije i sredine razreda.
b) Distribucija rezultata u k=6 razreda.
