Sve matematčke formule na jednom mestu

А

Л

Г

Е

Б

А

Р

С

К

И

И

З

Р

А

З

И

 

1

 

A B A

B

   

 

2

1

A B A

B

 

:

  

 

 

3

A B B A

  

(

закон

комутације

за

сабирање

)

A B B A

  

(

закон

комутације

за

множење

) 

 

4









A B

C

A

B C



  



   (

закон

асоцијације

за

сабирање

) 









A B C

A B C



  



           (

закон

асоцијације

за

множење

)  

 

5





A B C

A B A C





   

    (

закон

дистрибуције

множења

према

сабирању

) 





A B C

A C B C



    

   (

закон

дистрибуције

сабирања

према

множењу

) 

 

6









2

2

2

2

2

2

2

2

A B

A

AB B

A B

A

AB B

















   (

квадрат

бинома

) 

 

7









3

3

2

2

3

3

2

2

3

3

3

3

3

3

A B

A

A B

AB

B

A B

A

A B

AB

B





















   (

куб

бинома

) 

 

8







2

2

A

B

A B A B









   (

разлика

квадрата

) 

 

9









3

3

2

2

A

B

A B A

AB B











   (

збир

кубова

) 

 

10









3

3

2

2

A

B

A B A

AB B











   (

разлика

кубова

) 

 

11











4

4

2

2

A

B

A B A B A

B











Милош

Станић

                                                              1                                                    

Техничка

школа

Ужице

ОПЕРАЦИЈЕ

СА

СТЕПЕНИМА

чинилаца

...

n

n

a

a a a

a

    



n

a

(

степен

)

a    

(

основа

степена

)

n    

(

изложилац

степена

)






 

1

n

m

n m

a a

a

     (

множење

степена

једаких

основа

)







 

2

:

n

n

m

n m

m

a

a a

a

          (

дељење

степена

једнаких

основа

)

a







 

3

 

m

n

n m

a

a

     (

степеновање

степена

)





 

4

0

1

0

a

за

  a



 

 

5

1

1

n

n

n

a

(

превођење

степена

са

негативним

изложиоцем

у

a

a

степен

са

позитивним

изложиоцем

)



 





 

 

 

6









n

n

n

n

n

n

a b

a b       (

множење

степена

једнаких

изложилаца

)

a b

a b       (

степеновање

производа

)













 

7

n

n

n

n

n

n

a

a

   (

дељење

степена

једнаких

изложилаца

)

b

b

a

a

   (

степеновање

количника

)

b

b

 

  

 

  

 

 

Милош

Станић

                                                              2                                                    

Техничка

школа

Ужице

К

В

А

Д

Р

А

Т

Н

А

Ј

Е

Д

Н

Ч

И

Н

А

Квадратна

једначина

: 

2

0

Ax

Bx C



 

кој

има

канонски

облик

: 





2

0

A x







 

Милош

Станић

                                                              4                                                    

Техничка

школа

Ужице

где

је

:  

2

B

A







 









2

4

4

B

AC

A





 

и

решава

се

по

обрасцу

: 

2

1,2

4

2

B

B

AC

x

A

 





Бројеви

1

x

и

2

x

називају

се

решења

или

корени

квадратне

једначине

. 

Израз

2

4

B

AC



(

који

се

налази

под

кореном

у

претходном

обрасцу

) 

назива

се

дискриминанта

и

означава

са

D

 , 

то

јест

: 

2

4

D B

AC





Ако

је

0

D



онда

су

решења

1

и

2

x

x

реална

и

различита

.

Ако

је

0

D



онда

су

решења

1

и

2

x

x

реална

и

једнака

. 

Ако

је

0

D



онда

су

решења

1

и

2

x

x

конјуговано

комплексна

. 

Квадратни

трином

2

Ax

Bx C





се

раставља

на

чиниоце

по

обрасцу

: 







2

1

2

Ax

Bx C

A x x

x x



 





ВИЈЕТОВЕ

ФОРМУЛЕ

:

За

једначину

:  

2

0

Ax

Bx C



 

важе

Вијетове

формуле

: 

1

2

B

x

x

A







 









1

2

C

x x

A

 

Ако

једначину

2

0

Ax

Bx C



 

поделимо

са

добијамо

: 

A

2

2

0/ :

0

Ax

Bx C

A

B

C

x

x

A

A



 

 

 



 



 

 

 

 

Увођењем

смене

: 

и

B

C

p

q

A

A





добијамо

једначину

: 

2

x

px q

0



 

е

Вијетове

формуле

: 

за

коју

важ

 

1

2

x

x

p



 

1

2

x x

q

 

Милош

Станић

                                                              5                                                    

Техничка

школа

Ужице

Л

О

Г

А Р

И

Т

А

М

Дефиниција

логаритма

: 





log

0   

1   

0

def

x

a

b x

a

b

a

a

b





   





Специјално

: 

Ако

је

основа

логаритма

10

онда

се

тај

логаритам

назива

декадни

логаритам

и

означава

са

  log

b

, 

то

јест

: 

10

log

log

b

b



Ако

је

основа

логаритма

број

e

, 

где

је

...

2,7182818284590452353602874713527

e



односно

2,72

e



, 

онда

се

тај

логаритам

назива

Неперов

логаритам

или

природни

логаритам

и

означава

са

ln

b

то

јест

: 

ln

log

b

b



e

Својства

логаритма

:

 

log

a

b

a

b



1      

 

 

2           log

c

a

a

c



 





1

2

1

2

   log

log

g

a

a

a

b b

b

b







3    

lo

(

логаритам

производа

) 

 

1

1

2

2

4       log

a

b

 



log

log

a

a

b

b

b







 

    (

логаритам

количника

) 

 

 

5           log

log

n

a

a

b

n

 

b

   (

логаритам

степена

) 

 

6           log 1 0

a



( 

превођење

логаритма

са

основом

a

 

log

7

log

log

a

c

c

b

b

a



у

логаритам

са

произвољном

основом

c

 )                                 

На

основу

својства

може

се

доћи

до

следећих

својстава

: 

 

7

 

1

8

log

log

a

b

b

a



 

1

9

log

log

a

a

b

b

 

 

 

 

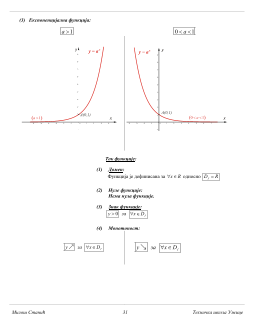
Милош

Станић

                                                              7                                                    

Техничка

школа

Ужице

sin 45

a

a

d

  

a

1

2

2

2

2





2

2

sin 45

cos 45

2

2

 



 

45

a

tg

 

a

1



45

1

45

1

tg

ctg

  

 

2

d

a



ву

добијених

резултата

можемо

формирати

таблицу

вредности

тригонометријских

фуннкција

за

углове

од



На

осно

30 ; 60 ; 45 .







30



45



60



1
2

2

2

3

2

sin



cos



3

2

2

2

1
2

tg



3

3

1

3

ctg



3

1

3

3