1
UNIVERZITET CRNE GORE
EKONOMSKI FAKULTET PODGORICA
SEMINARSKI RAD:
TEHNIKE ODLUČIVANJA U USLOVIMA
NEIZVJESNOSTI - TEORIJA IGARA
Podgorica, april, 2015.
2
SADRŽAJ
Uvod -----------------------------------------------------------------------------------------------------------3
Odlučivanje u uslovima izvjesnosti, rizika i neizvjesnosti ---------------------------------------------4
Odlučivanje u uslovima neizvjesnosti --------------------------------------------------------------------4
Teorija igara --------------------------------------------------------------------------------------------------8
Vrste igara-----------------------------------------------------------------------------------------------------9
Zatvorenikova dilema ----------------------------------------------------------------------------------------9
Nashova ravnotež -------------------------------------------------------------------------------------------11
Coca Cola – Pepsi -------------------------------------------------------------------------------------------11
Zaključak -----------------------------------------------------------------------------------------------------14
Literatura -----------------------------------------------------------------------------------------------------15
4
Odlucivanje u uslovima izvjesnosti, rizika i neizvjenosti
Odluke koje se donose danas realizovaće se u budućnosti (planiranje predhodi realizaciji).
Budućnost (okolnosti u preduzeću i okuženju) nekada se može sa preciznošću predvidjeti, nekada
govorimo o šansama da će se nešto desiti, a nekada nemamo nikakvu predstavu kakav će biti
razvoj događaja koji slijede.
Razlikujemo tri vrste uslova u kojima donosimo odluke. To su:
Odlučivanje u uslovima izvjenosti (sigurni smo u ishode odluka)
Odlučivanje u uslovima rizika (nijesmo sigurni, ali znamo kakve su nam šanse)
Odlučivanje u uslovima neizvjesnosti (ne znamo da li imamo šsanse i kolike su)
Primjer.Neka je data tabela br.1, u kojoj su prikayane četiri akcije izražene u novčanim dobicim
(u 000eura), pri realizaciji četiri moguća događaja. Tabela odlučivanja u kojoj su ishodi dati u
novčanom izrazu zove se tabela ili matrica plaćanja.
Akcije
Događaji
S1
S2
S3
S4
A1
1
5
16
4
A2
12
4
7
4
A3
9
9
5
5
A4
11
3
7
4
Tabela br.1
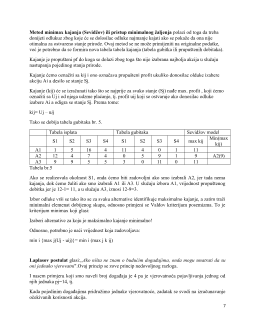
Odlučivanje u uslovima neizvjesnosti
U uslovima neizvjesnosti možemo da odredimo buduće događaje ali ne i vjerovatnoću njihovog
pojavljivanja. Ovakve situacije su za donosioca odluke veoma nepovoljne, ali su ponekad
neizbježne. Javljaju se po pravilu sa pojavom potpuno novih fenomena, srećemo ih u
istraživačkim projektima, prilikom uvođenja novog proizvoda, nove tehnologije, prilikom
nastupa na novo tržišste, kao i kod dugoročnih prognoza ekonomskih i političkih prilika u zemlji.
Metodi izbora koje primjenjujemo u uslovima neizvjesnosti su:
Optimistički (maxmax) metod
Pesimistički (max min) metod ili Valdov metod
Metod optimizma pesimizma ili Hurvicov metod
Metod minmax kajanja ili Sevidžov metod
Princip nedovoljnog razloga ili Laplasov metod
5
Optimistički (maximax) metod
sugeriše izbog alternative koja maksimizira rezultat. Polazi od
nerealne pretpostavke po kojoj bilo koja alternative da se preduzme ostvariće se najpovoljnija
situacija. Ide se na ,,sve ili ništa’’(najveći rizik).
Postupak se svodi na poređenje samo anjboljih rezultata svih alternativa i izbor najbolje među
njima. Zbog toga treba birati alternativu za koju je najpovoljniji ishod izabrane alternative, bolji
od najpovoljnijeg ishoda drugih alternativa. To je tkv. Kriterijum maximax , koji glasi:
Izaberi alternativu za koju je max profit po alternativama maksimalan.
Odnosno, potrebno je naći vrijednost koja zadovoljava
max
i
[max j (u
i
j
] gdje je
i
= 1,2,...m j= 1,2,...n
u
i
j predstavlja korisnost ishoda akcije Ai pri realizaciji događaja Sj.
Prema tome, za svaku alternativu Ai se identifikuje max efekat (profit), a zatim se u tako
dobijenom skupu bira max elemenat, tj. maksimalni profit. Alternativa koja odgovara toj
maksimalnoj vrijednosti je najpovoljnija.
Akcije
Događaji
Maxmin
S1
S2
S3
S4
Max j u ij
Max i(max
j u i)
A1
1
5
16
4
16
A1(16)
A2
12
4
7
4
12
A3
9
9
5
5
9
Tabela br. 2
Treća kolona sadrži najbolje ishode posmatranih akcija a njihovim međusobnim poređenjem
zaključujemo da je A1 najbolje opcija, po ovom metodu.
Ako se dogodi da dvije ili više akcija imaju identičan maksimalan ishod, postupak nastavljamo
tako što posmatramo samo prvoplasirane akcije i poredimo ih po njigovim drugim najboljim
ishodima. Ako ni tada ne donesemo odluku, proceduru ćemo ponavljati do konačnog izbora.
Pesimistički (maximin) metod ili Valdov metod
, nazvan je po autoru koji ga je formulisao.
Budući da donosilac odluke ne zna koja će se okolnost javiti pri realizaciji akcije, on zauzima
najoprezniji stav. On polazi od predpostavke da će se u budućnosti desiti najnepovoljnije stanje
okruženja. Zbog toga treba birati onu alternativu za koju je najnepovoljniji ishod izabrane
alternative, bolji od najnepovoljnijeg ishoda drugih alternativa. To je tzv. kriterijum maximin,
koji glasi:
Izaberi alternativu za koju je min profit po alternativama maksimalan!
Odnosno, potrebno je naći vrijednost koja zadovoljava uslov
Max
i
[min j (u
i
j)]
