
Tok funkcije Pregled
Милош Станић Техничка школа ‐ Ужицe
2007/2008
1
Испитвање
тока
функције
Испитивање
тока
функције
( )
y
f x
=
подразумева
да
се
аналитичким
путем
дође
до
сазнања
о
понашању
функције
,
као
и
њеним
значајним
тачкама
у
координантном
систему
,
те
да
се
на
основу
добијених
резултата
нацрта
график
те
функције
.
Дакле
потребно
је
испитати
:
(1)
(2)
(3)
И
ПРЕИОДИЧНОСТ
)
(4)
(5)
(6)
На
основу
добијених
резултата
нацртати
:
(7)
У
примеру
који
следи
биће
детаљно
описан
поступак
испитивања
тока
функције
као
и
сва
потребна
теоретска
објашњења
за
горе
наведене
ставке
,
почев
од
ДОМЕНА
ФУНКЦИЈЕ
до
ГРАФИКА
ФУНКЦИЈЕ
.
Кључну
улогу
код
испитивања
ТОКА
ФУНКЦИЈЕ
има
решавање
једначина
и
неједначина
,
наиме
,
помоћу
њих
ми
испитујемо
:
ДОМЕН
и
НУЛЕ
И
ЗНАК
ФУНКЦИЈЕ
.
Треба
свакако
нагласити
да
нуле
и
знак
испитујемо
три
пута
.
Први
пут
испитујемо
нуле
и
знак
финкције
( )
f x
Други
пут
испитујемо
нуле
и
знак
функције
( )
f x
′
да
бисмо
одредили
МОНОТОНОСТ
И
ЕКСТРЕМНЕ
ВРЕДНОСТИ
Трећи
пут
испитујемо
нуле
и
знак
функције
( )
f
x
′′
да
бисмо
одредили
КОНВЕКСНОСТ
;
КОНКАВНОСТ
;
и
ПРЕВОЈНЕ
ТАЧКЕ
.
ПРИМЕР
:
ИСПИТАТИ
ТОК
И
НА
ОСНОВУ
ДОБИЈЕНИХ
РЕЗУЛТАТА
НАЦРТАТИ
ГРАФИК
ФУНКЦИЈЕ
:
( )
3
2
3
x
f x
x
=
−
.
Miloš
Stani
ć
Digitally signed by Miloš
Stani
ć
DN: cn=Miloš Stani
ć
,
o=Tehni
č
ka škola Užice,
ou,
email=milos.chane@gmail
.com, c=YU
Date: 2010.02.07 00:16:25
+01'00'
Милош Станић Техничка школа ‐ Ужицe
2007/2008
2
( 1 )
Домен
(
област
дефинисаности
)
функције
Домен
функције
је
скуп
x
–
ова
за
које
је
израз
( )
y
f x
=
дефинисан
т
.
ј
.
треба
одредити
скуп
x
–
ова
за
које
је
могуће
израчунати
израз
Овде
ћемо
решити
дати
пример
.
Ако
желите
да
сазнате
више
кликните
на
:
(
>> )
Дата
функција
( )
3
2
3
x
f x
x
=
−
је
дефинисана
за
све
вредности
x
за
које
је
именилац
2
3
x
−
различит
од
нуле
,
односно
:
2
2
3
0
3
3
x
x
x
−
≠
≠
≠ ±
Дакле
домен
функције
је
:
(
) (
) (
)
,
3
3, 3
3,
f
D
= −∞ −
−
+∞
∪
∪
.
Другим
речима
:
Дата
функција
је
дрфинисана
за
(
) (
) (
)
,
3
3, 3
3,
x
∀ ∈ −∞ −
−
+∞
∪
∪
.
Шта
нам
говори
добијени
резултат
?
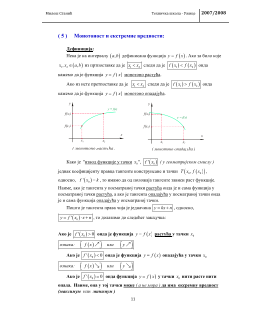
Овај
резултат
нам
говори
да
се
график
функције
налази
у
осенченом
делу
координантног
система
приказан
на
следећој
слици
:
(
>> )
Милош Станић Техничка школа ‐ Ужицe
2007/2008
4
У
том
смислу
,
треба
размотрити
постојање
вертикалне
,
хоризонталне
и
косе
асимптоте
.
Вертикална
асимптота
:
Ако
је
( )
lim
x a
f x
→
= ±∞
онда
је
права
x a
=
вертикална
асимптота
.
НАПОМЕНА
:
''
Кандидати
''
за
број
a
у
претходном
лимесу
су
тачке
прекида
или
крајеви
интервала
из
домена
функције
,
што
значи
да
вертикалних
асимптота
може
постојати
и
више
о
једне
.
Хоризонтална
асимптота
:
Ако
постоји
( )
lim
x
f x
b
→∞
=
онда
је
права
y b
=
хоризонтална
асимптота
.
Милош Станић Техничка школа ‐ Ужицe
2007/2008
5
Коса
асимптота
:
Ако
постоје
лимеси
:
( )
lim
x
f x
k
x
→∞
=
и
( )
lim
x
n
f x
k x
→∞
=
− ⋅
⎡
⎤
⎣
⎦
онда
је
права
y kx n
=
+
коса
асимптота
.
НАПОМЕНА
:
Хоризонтална
и
коса
асимптота
се
међусобно
искључују
(
ако
постоји
хоризонтална
онда
не
постоји
коса
асимптота
и
обрнуто
)
,
тачније
,
хоризонтална
асимптота
је
специјалан
случај
косе
асимптоте
код
које
је
0
k
=
односно
хоризонтална
асимптота
има
једначину
:
0
y
x n
= ⋅ +
.
Испитајмо
асимптоте
дате
функције
:
( )
3
2
3
x
f x
x
=
−
.
''
Вертикална
Асимптота
''
Пошто
имамао
две
тачке
прекида
:
( )
3
−
и
3 ,
то
значи
да
треба
испитати
граничне
вредности
функције
за
обе
тачке
:
( )
( )
( )
( )
( )
3
3
2
2
3
3
3
3 3
3 3
lim
lim
3
3 3
0
3
3
x
x
x
f x
x
→ −
→ −
−
−
−
=
=
=
=
= ∞
−
−
− −
Закључак
:
Права
( )
3
x
= −
је
вертикална
асимптота
Милош Станић Техничка школа ‐ Ужицe
2007/2008
7
( 3 )
Парност
функције
:
Дефиниција
:
Функција
у
= f(x)
je
парна
(
симетрична
у
односу
на
у
-
осу
)
ако
је
:
( )
( )
f
x
f x
− =
Дефиниција
:
Функција
у
= f(x)
je
непарна
(
симетрична
у
односу
на
координантни
почетак
)
ако
је
:
( )
( )
f
x
f x
− = −
Želiš da pročitaš svih 38 strana?
Prijavi se i preuzmi ceo dokument.
Slični dokumenti

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.


























































