Univerzitet u Prištini
Ekonomski fakultet
Kosovska Mitrovica
SEMINARSKI RAD
PREDMET:
OPERACIONA ISTRAŽIVANJA
TEMA:
TRANSPORTNI PROBLEMI:
OTVORENI I DEGENERISANI PROBLEM
Mentor: Student:
Kosovska Mitrovica, 2016. god.
4
1. TRANSPORTNI PROBLEM
Transportni problem obično predstavlja problem distribucije. Njime rešavamo problem
transporta te pronalazimo optimalni transportni plan koji ima minimalne transportne troškove
robe do odredišta. Rešenje transportnog problema sastoji se od utvrđenih količina koje se
dodeljuju različitim relacijama. Količine se kreću od nule (toj relaciji neće biti dodeljena ni jedna
količina), do maksimalne veličine, koja je jednaka manjoj od dve količine u redu (ponuda) i
koloni (potražnja). Količine se dodeljuju prema principu maksimalne moguće količine.
Problem transporta javlja se u praksi u različitim oblicima ovisno od broja vrsta jedinica koje se
prevoze ili raspoređuju, broju vrsta i tipova prevoznih sredstava, kao i broju ishodišta i odredišta
ili pak načinu prevoza. Transportni problem je takva vrsta problema za koji je potrebno
programirati prevoz, odnosno odrediti broj homogenih (istovrsnih) jedinica (tereta, predmeta,
osoba, …) koje treba prevesti, odnosno rasporediti iz više ishodišta (mesta gde se nalaze
jedinice) na više odredišta (mesta na kojima se podmiruje potražnja, odnosno zadovoljava
zahtev) s ciljem da troškovi prevoza (ili udaljenost, vreme, …) budu minimalni, odnosno iznosi
prihoda (dobiti, …) maksimalni. Pritom treba uzeti u obzir da ponuda pojedinih ishodišta ne sme
biti premašena i da potražnja svih odredišta treba biti zadovoljena.
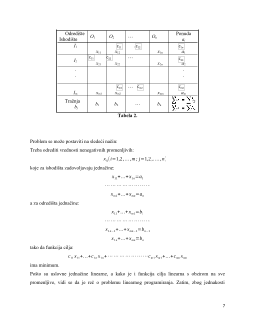
Svakom transportnom problemu pripada odgovarajuća matrica transporta koja izgleda ovako:
Tabela 1:
Matrica transporta
Odredište
Ishodište
O
1
O
2
O
n
Ponuda
a
i
I
1
x
11
x
12
. . .
x
1n
a
1
I
2
x
21
x
22
x
2n
a
2
.
.
.
.
I
m
x
m1
x
m2
x
mn
a
m
Tražnja
b
j
b
1
b
2
b
n
Oznake u matrici:
c
2
n
c
1
n
m
c
11
c
12
c
22
c
21
c
m
1
c
m
2
c
mn
5
m
–
ukupan broj ishodišta (otpremnih stanica);
i
–
redni broj ishodišta,
i
=
1,2
, … , m
;
n
–
ukupan broj odredišta (prijemnih stanica);
j
–
redni broj odredišta,
j
=
1,2
, … , n ;
c
ij
–
trošak prevoza (udaljenost, vreme ili iznos prihoda, dobiti) jedne jedinice na relaciji od
i
-
tog ishodišta do
j
-tog odredišta;
x
ij
–
količina (ili iznos) koju treba prevesti, preneti ili rasporediti iz
i
-tog ishodišta u
j
-to
odredište
a
i
–
količina koja se raspoređuje iz pojedinih ishodišta (ponuda ishodišta)
b
j
–
količina koja je potrebna pojedinom odredištu (tražnja odredišta).
Na temelju matrice transporta postavlja se matematički model koji se sastoji od funkcije
kriterijuma i ograničenja. Matematički model transportnog problema glasi:
T
=
∑
i
=
1
m
∑
j
=
1
n
c
ij
x
ij
uz ograničenja
Model u kome je
odnosi se na
zatvoreni transportni problem
, za razliku od
otvorenog transportnog problema
za koji je ukupna ponuda svih ishodišta veća ili manja od
ukupne tražnje (
).
Teorema 1.
Transportni zadatak ima optimalno rešenje ako je ukupna ponuda jednaka ukupnoj
traznji.
Dokaz:
Ako transportni zadatak ima optimalno rešanje, onda za optimalne
x
ij
važi
