1
ТРИГОНОМЕТРИЈСКЕ ФУНКЦИЈЕ
Једначина јединичне кружне линије
Нека је у равни τ задат Декартов правоугли координатни систем координатним
почетком О и међусобним нормалним јединичним векторима
⃗
i
и
⃗
j
, при чему се,
посматрано са изабране стране равни τ, вектор
⃗
j
добија ако се вектор
⃗
i
обрне око
заједничког почетка О за прав угао у смеру супротном од смера кретања казаљке на
сату (такав смер смо назвали позитивним). Важно је напоменути да је ово релативан
појам, па се не сме испустити из вида да раван посматрамо са изабране стране. Заиста,
замислимо модел равни који је прозиран и два посматрача који се налазе на супротним
странама те равни. Ако један од њих уочи да се вектор
⃗
i
обрће према вектору
⃗
j
у
позитивном смеру, другоме ће исто кретање бити обртање у негативном смеру (сл.1)
сл. 1
За сваки вектор
⃗
ν
у равни τ постаје јединствени реални бројеви x и y, такви да важи:
⃗
ν
=
x
⃗
i
+
y
⃗
j
,
што записујемо и у облику
⃗
ν
=(
x , y
)
.
Ако тачка М припада равни τ, онда вектор
⃗
OM
називамо вектором положаја тачке М. Ако је, при томе:
⃗
OM
=
x
⃗
i
+
y
⃗
j
онда x и y зовемо координате тачке М, што означавамо
М
(
x , y
)
.
Интензитет овог
вектора , дакле, растојање између тачке О и М, је
d
(
O , M
)=
|
⃗
OM
|
=
√
x
2
+
y
2
.
Знамо да је кружна линија у равни τ полипречника 1 са центром О, ознака к(0,1),
скуп свих тачака у равни τ које су на растојању 1 од тачке О. Дакле, тачка
М(x,y)припада кружној линији к(0,1) ако и само ако је d(0,М)=1, што, имајући у виду
раније речено, можемо исказати овако:
2
M
(
x , y
)
ϵ k
ако и само ако је
√
x
2
+
y
2
=
1
Последња једначина еквивалентна је једначинама
x
2
+
y
2
=
1
, чиме је доказана следећа
теорема:
Теорема 1
. Једначина кружне линије у равни xOy полупречника 1 са центром О
је:
x
2
+
y
2
=
1
.
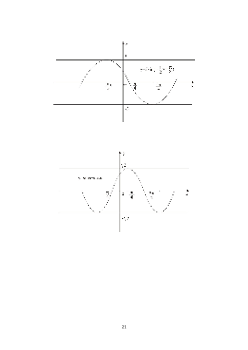
сл.2 сл.3
Радијанска мера угла
Обим круга полупречника R (дужина лука кружне линије која представља
границу тог круга) једнак је 2Rπ, где је π одређени реалан број, π
≈
3,14
. Одакле следи
да је обим јединичног круга једнак 2π. Исто тако, знамо да је дужина кружног лука
кружне линије полупречника R који одговара централном углу чија је мера
φ
о
=(
0
≤ φ
<
360
)
једнака
πφ
180
R ;
за јединичну кружну линију та дужина једнака је
πφ
180
.
Уведимо сада нову јединицу мере углова.
Дефиниција 1. Нека је дата кружна линија полупречника R, k (O,R).Мера
централног угла који одговара луку дужине R те кружне линије је један радијан.
Имајући у виду до сада речено, јасно је да пун угао има 2π радијана. одатле
следи да је мера у степенима угла од једног радијана једнака:
1
rad
=(
360
o
2
π
)=(
180
o
π
)
≈
57
o
17
'
45
' '
сл. 4
УОПШТЕЊЕ ПОЈМА УГЛА
Уопштење појма кружног лука
4
позитивно оријентисан. Дужина овог уопштеног лука једнака је 2mπ+l, где је l дужина
позитивно оријентисаног лука од А до Р. На исти начин, ако из тачке А треба прећи у
тачку Р крећући се по k у негативном смеру, то можемо остварити тако што ћемо
проћи негативно оријентисани лук АР кружне линије k или тако што ћемо известан
број пута, рецимо n пута, где је n неки природни број, обићи у негативном смеру целу
кружну линију k, а затим проћи још и негативно оријентисани лук АР линије k. Сваки
од овако добијених путева је уопштени лук кружне линије k од А до Р, негативно
оријентисан; његова је дужина једнака 2nπ+l, где је l дужина негативно оријентисаног
лука од А до Р.
Два уопштена лука кружне линије k једнака су ако се могу превести један у
други ротацијом те кружне линије око њеног центра О. Таква два уопштена лука имају
исте оријентације и једнаке су дужине. Збиром двају уопштених лукова кружне линије
k назива се кружни лук који се добија надовезивањем другог уопштеног кружног лука
на први. При томе ће збир двају позитивно оријентисаних уопштених кружних лукова
бити позитивно оријентисан кружни лук, док ће збир двају негативно оријентисаних
кружних лукова бити негативно оријентисан кружни лук. Збир двају супротно
оријентисаних уопштених кружних лукова кружне линије k биће позитивно
оријентисани лук у случају да је дужина позитивно оријентисано ,,сабирка“ већа, а
негативно оријентисан у случају да је већа дужина негативног
оријентисаног ,,сабирка“; дужина му је једнака апсолутној вредности разлике
дужина ,,сабирака“.
Проширићемо пресликавање Е до пресликавања скупа реалних бројева на скуп
тачака једначине кружне линије k. Посматрамо опет у равни xOy јединичну кружну
линију k са центром О и нека је
τ
права у тој равни која садржи тачку А(0,1) и
нормална је на осу Ox. Претпоставимо да
τ
оса реалних бројева на којој је изабрана
тачка А за почетак, усвојем смер који се поклапа са позитивном смером осе Oy и
јединица мерења се поклапа са једницом мерења у систему xOy. Позитивна тачка T(1,t)
одређена је својом ординатом t; исто тако, сваком реалном броју t одговара одређена
тачка осе
τ
. Замислимо, као на почетку овог поглавља модел осе
τ
који се састоји од
нерастегљивог конца и модел кружне линије од ,,чврстог материјала”. Конац можемо
намотати око k на начин приказан на сл. 6. Произвољан реалан број t одређује тачку
T(1,t) осе
τ
. Ако је t>0, тачки Т одговараће уопштени кружни лук кружне линије k који
је позитивно оријентисан и дужина му је једнака t. Ако је t<0, тачки Т одговараће
уопштени кружни лук кружне линије k који је негативно оријентисан и дужина му је
једнака –t. Броју t=0 одговара тачка А; она се не помера при нашем намотавању па се
прескиава у себе. На овај начин дефинисали смо пресликавање:
Е
:
R → k .
Једначина кружне линије k тиме, по аналогији са осом реалних бројева, постаје
јединична кружна линија реалних бројева.
5
Сл.6
Уопштење појма угла
Нека је у равни xOy дата јединична кружна линија k са центром О. Посматрајмо
ротацију те равни са центром ротације О. Нека полуправа Ox сече k у тачки А. Ако
раван ротирамо у позитивном смеру (у смеру супротном од смера казаљке на сату) за
неки угао φ, при чему је мера тог угла мања од
360
о
(радијанска мера мања од 2π
радијана), полуправа ће ,,проћи“ кроз све тачке области тог угла, а тачка А описаће
кружни лук кружне линије k која одговара централном углу φ. Ако је t радијанска мера
угла φ, дужина кружног лука који опише тачка А биће t. Јасно је да у овом случају
кружни лук који опише тачка А одређује угао φ. Ако раван ротирамо у негативном
смислу, добићемо негативно оријентисани кружни лук који прође тачка А. И у овом
случају кружни лук који прође тачка А одређује угао ротације; тај угао је оријентисан
негативно, па кажемо да је раван ротирана за негативни угао.
