Trozglobni lukovi i okviri (1)
V. S. & K. F.
1.
Opis. Nepromjenjivost i odredenost
Trozglobni
su
nosaˇ
ci
konstrukcijski sistemi sastavljeni od dvaju diskova koji mogu biti
punostjeni ili reˇsetkasti. Diskovi su medusobno povezani zglobom, a svaki je disk zglobno
vezan i za podlogu. Zglob koji povezuje diskove nazvat ´cemo srednjim zglobom. Leˇzajni
zglobovi mogu, ali ne moraju biti na istoj visini. Ako su osi diskova dijelovi krivulja,
nosaˇci se obiˇcno nazivaju
trozglobnim lukovima
(slike 1.a. i b.), a ako su osi poligonalne
linije
trozglobnim okvirima
(slike 1.c. i d.). Osim toga, osi diskova mogu biti i samo na
dijelu zakrivljene (slika 1.e.). Najviˇsu toˇcku luka nazivamo tjemenom.
a.
b.
c.
d.
e.
Slika 1.
Trozglobni se sistemi ˇcesto upotrebljavaju kao glavni nosaˇci tvorniˇckih hala, skladiˇsta,
sportskih dvorana, mostova (primjerice slike 2. i 3.), . . . , a izvode se od armiranoga betona,
ˇcelika te monolitnog ili lijepljenog lameliranog drva. Osim zbog ˇsiroke rasprostranjenosti
u primjenama, trozglobni su nosaˇci vrlo vaˇzna skupina konstrukcija i s teorijskoga i s
edukacijskog glediˇsta: kao ˇsto ´cemo u sljede´cim odjeljcima pokazati, nosaˇci koji pripadaju
nekim drugim tipovima proraˇcunavaju se svodenjem na njih ili prema analogiji s njima.
Trozglobni sistemi zadovoljavaju nuˇzdan uvjet geometrijske nepromjenjivosti:
S
n
D
3
n
Z
1
2
n
L
2
3
1
2
2
2
0
.
1
Slika 2. Pont Alexandre III, Pariz
(J. Cassien–Bernard, G. Cousin, J. R´esal i A. Alby; 1896.–1900.)
Slika 3. Viaduc d’Austerlitz, Pariz
(J.–C. Formig´e, F. Bienven¨
ue, L. Biete i M. Koechlin; 1904.)
2
P
A
B
C
a.
C
B
B
C
b.
P
B
A
c.
P
A
B
A
N
1
T
1
M
1
t
1
d
1
A
N
1
T
1
M
1
=
A
·
d
1
d.
P
B
N
1
T
1
M
1
R
B,P
P
R
B,P
B
N
1
T
1
e.
Slika 5.
poznata (poznati su joj i pravac djelovanja i vrijednost), drugoj (
B
) znamo pravac djelo-
vanja, a za tre´cu (
A
) znamo kojom toˇckom prolazi. Ravnoteˇza je mogu´ca samo ako pravci
djelovanja sve tri sile prolaze istom toˇckom (prvi geometrijski uvjet ravnoteˇze triju sila).
Time je odreden pravac djelovanja reakcije
A
: on mora u planu poloˇzaja pro´ci sjeciˇstem
pravaca djelovanja sila
P
i
B
(lijevi crteˇz na slici 5.c.). Drugi geometrijski uvjet ravnoteˇze
triju sila —trokut sila mora biti zatvoren — daje intenzitete i smisao djelovanja reakcija
A
i
B
(desni crteˇz na slici 5.c.).
Kad su poznate reakcije, mogu se metodom jednostavnih presjeka odrediti sile u oda-
branom popreˇcnom presjeku. Priˇca je ve´c poznata: zamiˇsljenim presjekom odvajamo dio
nosaˇca pa sile u presjeku moraju uravnoteˇziti rezultantu svih ostalih sila koje djeluju
na promatrani dio. U naˇsem primjeru na dio lijevo od presjeka djeluje samo reakcija
A
(slika 5.d.), dok za dio desno od presjeka treba odrediti rezultantu
R
B
,
P
zadane sile
P
i
reakcije
B
(slika 5.e.). Sila
R
B
,
P
ima isti intenzitet i isti pravac djelovanja kao sila
A
, a
suprotni smisao.
4
Postupak se nimalo ne razlikuje od grafiˇckoga postupka odredivanja sila u odabranom
presjeku nosaˇca s jednim diskom, opisana na stranicama 22. i 23. poglavlja
Statiˇ
cki odredeni
nosaˇ
ci s jednim punostjenim diskom
(
1
): budu´ci da su pravci djelovanja uzduˇzne i popreˇcne
sile poznati — uzduˇzna leˇzi na pravcu tangente
t
1
na os nosaˇca u toˇcki presjeka, a popreˇcna
na okomici na tu tangentu — njihove intenzitete i smisao dobivamo zatvaranjem trokuta
sila. Uravnoteˇzavanjem dijelova nosaˇca lijevo i desno od presjeka dobivamo, kao ˇsto znamo,
sile jednakih intenziteta, ali suprotnih orijentacija.
2
Treba, stoga, uz crteˇz uvijek jasno
navesti na koji dio dobivene sile djeluju, posebno ako se promatrani dio ne crta izdvojeno
(ˇsto ´ce i biti sluˇcaj u ve´cini primjera koji slijede).
Intenzitet momenta savijanja
M
1
jednak je umnoˇsku intenziteta rezultante koja djeluje
na promatrani dio i udaljenosti
d
1
pravca njena djelovanja od teˇziˇsta presjeka:
M
1
A
d
1
R
B,P
d
1
;
udaljenost
d
1
oˇcitavamo u planu poloˇzaja. Smisao vrtnje momenta
M
1
suprotan je od
smisla vrtnje momenta rezultante u odnosu na teˇziˇste presjeka (u naˇsem je primjeru jednak
pretpostavljenom). I za smisao vrtnje momenata koji djeluju na lijevi i na desni dio vrijedi
ono ˇsto je reˇceno za smisao djelovanja sila
N
1
i
T
1
.
Viˇ
se sila zadanih na jednom disku.
U primjeru smo, jednostavnosti opisa radi, uzeli
da je zadana samo jedna sila. ˇ
Sto se odredivanja reakcija tiˇce, sila
P
moˇze biti i rezultanta
viˇse sila, ali, naglaˇsavamo, sve moraju djelovati na jedan disk — reakcija u leˇzaju drugoga
diska prolazit ´ce kroz srednji zglob samo ako je taj disk neoptere´cen. I za odredivanje sila
u presjecima neoptere´cenoga diska svejedno je je li sila
P
jedina ili je rezultanta viˇse sila.
Uz to, niˇsta se u postupku ne mijenja ni pri odredivanju sila u presjecima optere´cenoga
diska koji leˇze lijevo od prve ili desno od zadnje sile zadanoga niza sila. Jedino za pre-
sjeke izmedu tih sila treba u obzir uzeti pravce djelovanja, odnosno hvatiˇsta pojedinih
sila —uravnoteˇzuju se samo one sile koje djeluju na dio nosaˇca lijevo ili na dio desno od
odabranoga presjeka.
Primjerice, na lijevi disk luka sa slike 6. djeluju sile
P
1
i
P
2
. Kako je desni disk neopte-
re´cen, pravac djelovanja reakcije
B
i sada prolazi kroz zglob
C
. Pravac na kojem djeluje
reakcija
A
prolazi kroz sjeciˇste pravaca djelovanjˆa reakcije
B
i rezultante
P
sila
P
1
i
P
2
. U
poligonu sila moˇzemo oˇcitati intenzitete i orijentacije reakcija
A
i
B
. Za sada niˇsta novo.
Presjek 1
1 odabrat ´cemo izmedu hvatiˇstˆa sila
P
1
i
P
2
. Na dio lijevo od tog presjeka
djeluju sile
A
i
P
1
(s``
amo sile
A
i
P
1
, iako je prema crteˇzu i hvatiˇste rezultante
P
na tom
dijelu), a na dio desno od njega reakcija
B
i sila
P
2
. Promatramo li lijevi dio, sile u pre-
sjeku 1
1 moraju, dakle, uravnoteˇziti rezultantu
R
A
,
P
1
sila
A
i
P
1
. Nagib pravca djelovanja,
intenzitet i orijentaciju te rezultante odredujemo u poligonu sila. Uz poznatu silu
R
A
,
P
1
, u
2
Prisjetite se: suprotne orijentacije sila znaˇce da sile u odnosu na ravnine popreˇcnih presjeka jednako
djeluju i da njihove vrijednosti u tehniˇckom zapisu imaju iste predznake — uzduˇzna je sila u naˇsem primjeru
tlaˇcna pa je njena vrijednost, prema dogovoru o predznacima vrijednostˆı sila u presjeku, negativna.
5
P
1
P
2
P
3
a.
=
P
1
P
2
b.
+
P
3
c.
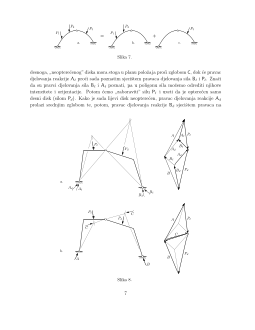
Slika 7.
desnoga,
”
neoptere´cenog” diska mora stoga u planu poloˇzaja pro´ci zglobom
C
, dok ´ce pravac
djelovanja reakcije
A
`
pro´ci sada poznatim sjeciˇstem pravaca djelovanja sila
B
`
i
P
`
. Znaˇci
da su pravci djelovanja sila
B
`
i
A
`
poznati, pa u poligonu sila moˇzemo odrediti njihove
intenzitete i orijentacije. Potom ´cemo
”
zaboraviti” silu
P
`
i uzeti da je optere´cen samo
desni disk (silom
P
d
). Kako je sada lijevi disk neoptere´cen, pravac djelovanja reakcije
A
d
prolazi srednjim zglobom te, potom, pravac djelovanja reakcije
B
d
sjeciˇstem pravaca na
P
`
P
d
B
`
A
`
A
d
B
d
P
`
P
d
B
`
A
`
B
d
A
d
B
`
A
d
B
A
a.
P
`
P
d
P
`
P
d
B
A
C
A
B
C
C
b.
Slika 8.
7
