Неготинска гимназија
Лука Лечић
Садржај
1. Увод
1.1.
Појам вектора и скалара
1.2.
Вектори
1.3.
Елементи вектора
2. Врсте вектора
3. Важни појмови
3.1.
Нулти вектор
3.2.
Орт вектор
3.3.
Јединични вектор
3.4.
Колинеарни вектори
3.5.
Компланарни вектори
Пројекција вектора
4. Координате вектора
5. Линеарна зависност
6. Производи вектора
6.1.
Скаларни производ вектора
7. Векторски производ вектора
8. Мешовити производ
9. Задаци
10. Примена вектора
11. Литература
1
Неготинска гимназија
Лука Лечић
1.
Увод
1.1.
Појам вектора и скалара
Величине које су одређене само својом бројном вредношће и одговарајућом
јединицом су скаларне величине или кратко скалари. Скаларне величине су на пример:
дужина, површина, запремина, температура, маса итд.
Величине које су одређене својом бројном вредношћу (интензитетом), правцем и
смером називају се векторске величине или кратко вектори. Векторске величине су: сила,
брзина, убрзање, импулс итд.
Векторске величине графички представљамо оријентисаним одсечком праве чија
дужина одговара интезитету вектора, правац тог одсечка одређује правац вектора, а
стрелица његов смер.
1.2.
Вектори
Векторске величине су величине одеђене са три или више параметара.
Најпознатији су примери везани за геометрију у простору где се вектор одређује правцем,
смером и интензитетом, а представља стрелицом оријентисаном дуж правца, дужине
пропорционалне интензитету, а чији врх показује смер на заданом правцу.
Сл.1. Вектор
У геометрији векторима називамо оријентисани одсечак тј. део праве ограничен
двема тачкама од којих је једна почетна, а друга крајња. Рецимо да су то А и В из Р
н
, тада
је:
=
, а
=
,
, a
2
Неготинска гимназија
Лука Лечић
Сл.2. Репрезентативни вектор
3.
Важни појмови
3.1.
Нулти вектор
Нулти вектор
a
0
је вектор ћији је интензитет једнак нули. Означава се као нула са
назнаком за вектор.
=0
- вектор дужине 0;
- ознака: ;
- вредност:
= =
= …;
- интензитет нултог вектора: = 0.
3.2.
Орт вектор
- вектор дужине 1,
- ознака:
,
;
- интензитет орта:
=1.
Такође се може бележити у складу са координатним системом, орт у правцу х-осе
, у правцу у-осе , и у правцу z-осе .
3.3.
Јединични вектор
4
Неготинска гимназија
Лука Лечић
Јединични вектор је вектор чији је интензитет једнак јединици. За сваки не-нулти
вектор се може одредити одговарајући јединични вектор исте оријентације и смера.
При чему је:
-
- Задани вектор
-
- Интензитет вектора
-
-
Је вектор који има исти смер као , а дужина му је 1,
Овај поступак се зове нормирање вектора.
3.4.
Радијус вектор
Ако је Т нека тачка простора, а О тачка координатног почетка. Вектор називамо
радијус вектор тачке Т. Записујемо га са .
a =
, b =
За сваки вектор можемо изабрати његовог представника тако да му почетна тачка
буде баш тачка координатног почетка тј. О. На тај начин се добија радијус вектор неке
(било које) тачке.
5
Неготинска гимназија
Лука Лечић
-
Ортогонална пројекција у равни на правац р је функција која свакој тачки А
равни придружује тачку у којој вертикала на р, која пролази тачком А, сече
правац р
-
Ортогонална пројекција у простору на правац р је функција која свакој тачки А
простора придружује тачку у којој раван која пролази тачком А, а вертикална је
на р, сече правац р .
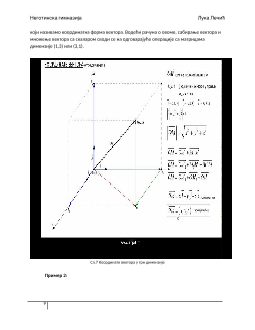
Сл.5. Пројекција вектора на вектор. Интензитет овог вектора је: Ц = Б цос
Сл.6.а и 6.б Пројекција вектора на праву х
4.
Координате вектора
Увођењем координатног система омогућава представљање вектора помоћу
реалних бројева. На тај начин се поједностављује руковање са векторима, јер се
операције са векторима своде на одговарајуче операције са бројевима.
Познато је да свакој тачки у равни додељује уређен пар реалних
бројева
(х,у), тј.
њене координате у Декадном координатном систему. Сличан поступак се може
применити и за тачке простора.
7
