
Statika konstrukcije 1
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
Predmet:
Teorija konstrukcija 1
Predmetni nastavnik:
emer. prof. dr. Ognjen Jokanovi
ć
, dipl.inž.gra
đ
.
Predmetni asistent:
viši asistent mr. Rašid Hadžovi
ć
, dipl.inž.gra
đ
.
Nastavni plan i program:
¾
Statika konstrukcija. Prora
č
unske šeme.
¾
Optere
ć
enja konstrukcija. Oslonci ravanskih konstrukcija.
¾
Unutrašnje i vanjske sile. Povezanost izme
đ
u optere
ć
enja, transverzalnih sila i momenata
savijanja.
¾
Stati
č
ka odre
đ
enost sistema. Kinemati
č
ka stabilnost nosa
č
a.
¾
Stati
č
ki odre
đ
eni sistemi.
¾
Puni nosa
č
i.Prosta greda. Konzola. Grede sa prepustom.
¾
Uticajne linije za sve pune nosa
č
e. Stati
č
ki i kinemati
č
ki na
č
ini rješavanja uticajnih linija.
¾
Gerberove grede. Uticajne linije kod Gerberovih greda.
¾
Luk sa tri zgloba. Uticajne linije lukova sa tri zgloba.
¾
Rešetkasti nosa
č
i. Uticajne linije rešetkastih nosa
č
a.
¾
Virtuelna pomjeranja. Virtuelni rad.
¾
Energetske teoreme.
Literatura:
Statika konstrukcija I (1. i 2. dio), Ing.
Đ
or
đ
e Solovjev,
Uslov izlaska na ispit:
Ta
č
no ura
đ
eni i predati programski zadaci. Potpis predmetnog
nastavnika.
Pored programskih zadataka, svaki student je u obavezi da uradi 4 zadatka iz izu
č
avanih oblasti,
koje
ć
e zadati asistent i koje
ć
e prezentirati ostalim kolegama u sklopu vježbi. Zadaci
ć
e biti
ocjenjivani i ocjena
ć
e imati uticaj na ocjenu iz pismenog dijela ispita, tako da student može na
osnovu tih zadataka da dobije od -5 (minus 5 = ako ne bude uradio nijedan od datih zadataka ili
ih loše prezentirao) do +5 bodova(plus 5=ako svi zadaci budu ura
đ
eni i prezentirani valjano).
Tokom godine studenti su obavezni da aktivno u
č
estvuju u nastavi, da postavljaju pitanja, kao i
da odgovaraju na postavljena pitanja. Zalaganje u nastavi
ć
e tako
đ
er biti ocjenjeno i ima
ć
e uticaj
na ocjenu iz pismenog dijela ispita do
±
5 bodova. Svi odgovori pozitivni i negativni
ć
e biti
evidentirani, te
ć
e se na osnovu istih dati zasluženi broj bodova.
Tokom godine
ć
e biti vo
đ
ena evidencija o prisustvu studenata, tako da svaki student koji bude
odsutan preko 30 % iz nastave ne
ć
e imati pravo na potpis predmetnog nastavnika.
Na
č
in polaganja ispita:
Pismeni i usmeni dio ispita.
Pismeni dio ispita se polaže integralno iz svih oblasti koje su izu
č
avane tokom godine. Ispit se
smatra položenim ako je student dobio 55 bodova i više.
Usmeni dio ispita se polaže nakon položenog pismenog dijela. Vrijeme polaganja usmenog dijela
ispita se se dogovara sa nastavnim profesorom.
Ostalo:
U sklopu vježbi studenti
ć
e i
ć
i sa predmetnim nastavnikom u obilazak gra
đ
evinskih
objekata u izgradnji i diskutovati o istim, razmatrati stati
č
ke šeme i optere
ć
enja na konstrukcije,
razgovarati o problemima gra
đ
enja konstrukcija i rješenjima istih.
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
UVOD
Skup ta
č
aka me
đ
usobno povezanih u jednu cjelinu zovemo
nosa
č
.
Zadatak nosa
č
a je da
obezbijedi nepomjerljivost izvjesnih ta
č
aka me
đ
usobno i u odnosu na stalne ta
č
ke u prostoru. To
se naj
č
eš
ć
e postiže pravilnim komponovanjem više linijskih nosa
č
a koji svaki za sebe ima
ograni
č
enu ulogu da samo obezbijedi stabilnost u svojoj ravni, a svi zajedno obezbje
đ
uju
prostornu stabilnost. Nosa
č
i koji obezbje
đ
uju samo nepomjerljivost u svojoj ravni zovemo
ravnim linijskim nosa
č
ima
, dok nosa
č
i koji onemogu
ć
vaju nepomjerljivost u prostoru zovemo
prostornim linijskim nosa
č
ima.
Elementi nosa
č
a su:
1) Štapovi
2) Kruti uglovi
3) Oslonci
Štapovi su prave ili krive linije koje se nalaze u geometrijskim mjestima težišta popre
č
nih
presjeka nekog nosa
č
a. Ukoliko su dimenzije popre
č
nih presjeka male u odnosu na dužinu
štapova, tako da štap može da primi samo aksijalno optere
ć
enje, zovemo ga
prostim štapom.
Ako popre
č
ni presjek ima dimenziju da može da primi i druga optere
ć
enja pored aksijalnih
zovemo ga
greda.
Štapovi mogu biti spojeni zglobno ili kruto.
θ
θ
θ
θ
θ
Zglobna
veza
Kruta
veza
Č
vor je ta
č
ka u kome se spajaju 2 ili više štapova ili je to slobodan ilil oslonjen kraj
štapa. Sa brojem
č
vorova raste i broj štapova i krutih uglova i zbog toga prora
č
un i brojanje
elemenata se otežava, a nama je cilj da to brojanje smanjimo i na taj na
č
in da smanjimo sebi
prora
č
un. Strukturno linijske nosa
č
e dijelimo na
rešetkaste i pune nosa
č
e.
Rešetkasti linjski nosa
č
sastoji se samo od prostih štapova i oslonaca.
Puni nosa
č
je nosa
č
sastavljen od štapova greda i prostih štapova i oslonaca sa ili bez krutih
uglova.
KINEMATI
Č
KA STABILNOST NOSA
Č
A
Da bi sistem štapova
č
inio nosa
č
potrebno je da se
č
vorovi ne pomjeraju bez deformacija štapova
pomjeranja oslonaca i okretanja uklještenja. Za takav sistem štapova kažemo da je
kinemati
č
ki
stabilan.
U suprotnom sistem je
kinemati
č
ki labilan.
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
Ako izme
đ
u dva štapa postavimo kruti ugao u
č
voru
l
dobivamo krutu plo
č
u od štapova
il
i
lk
i dobivamo 3 stepena slobode pomjeranja.
Zna
č
i da
Zk krutih uglova
ukida
Zk stepeni
slobode pomjeranja.
Ako sada oslonimo neki štap
ik
na pokretni
oslonac (tj. pravac oslanjanja je paralelan sa y-
osom, pa je prema tome
y
i
= const.
, dok
x
i
, x
k
, y
k
nisu me
đ
usobno nezavisne ve
ć
moraju da
zadovolje uslov nepomjerljivosti dužine
l
ik
–
udaljenost ta
č
aka
i
i
k
), stoga ta
č
ke
i
i
k
pri
ovakvoj vezi i oslanjanju imaju 2 stepena
slobode pomjeranja. Zna
č
i da je oslonac
ukinuo jedan stepen slobode pomjeranja.
Prema tome Zo oslonaca ukida Zo stepeni
slobode pomjeranja
č
vorova.
Time je pokazano da svaki element
nosa
č
a ukida po jedan stepen slobode
pomjeranja. Svi elementi nosa
č
a ukidaju
ukupno
Zs + Zk + Zo – stepeni slobode pomjeranja
Zs + Zk + Zo = 2k ; ako nosa
č
zadovoljava ovu jedna
č
inu kažemo da je
prosto kinemati
č
ki
stabilan.
Za nosa
č
e kod kojih je:
Zs + Zk + Zo > 2k
kažemo da su
višestruko kinemati
č
ki stabilni,
A kod kojih je:
n = Zs + Zk + Zo - 2k > 0
kažemo da su
labilni.
Ovdje je n – broj suvišnih elemenata za prostu kinematsku stabilnost.
Pri definisanju nosa
č
a moramo paziti i na pravilan raspored elemenata.
Primjer 1:
7
8
9
10
11
12
1
6
2
3
4
5
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
k = 12
Zs = 21
Zk = 0
Zo = 3
Σ
Z = 24 = 2k
Nepravilan raspored elemenata nosa
č
a dovodi do toga da je ovaj sistem
labilan
.
1-3-7-9 dio prestavlja krutu plo
č
u koja je vezana štapovima 3-4- i 9-10 za drugu krutu plo
č
u 4-6-
10-12. Iz kinematike je poznato da je
č
etverougao zglobno vezanih štapova predstavlja labilnu
figuru, a to je slu
č
aj na
č
vorovima 3-4-9-10.
Primjer 2:
k = 3
Zs = 2
Zk = 0
Zo = 4
Σ
Z = 6 = 2k
Sistem je u kriti
č
noj konfiguraciji zbog toga što i najmanje optere
ć
enje izaziva znatne
deformacije koje nisu zanemarljive u odnosu na deformaciju štapa.
UNUTRAŠNJA KINEMATI
Č
KA STABILNOST
Za
štapove i krute uglove
kažemo da su
unutrašnji elementi nosa
č
a
, jer spre
č
avaju relativno
pomjeranje
č
vorova.
Za takve nosa
č
e kod kojih unutrašnji elementi spre
č
avaju relativno pomjeranje
č
vorova kažemo
da su unutrašnje stabilni i da
č
ine jednu
krutu plo
č
u.
Kako jedna kruta plo
č
a ima 3 stepena slobode pomjeranja u ravni broj unutrašnjih elemenata
nosa
č
a za prostu kinemati
č
ku stabilnost treba da je:
Zs + Zk
≥
2k – 3
PRAVILAN RASPORED ELEMENATA
NOSA
Č
A
k = 5
Zs = 4
Zk = 3
Zs + Zk = 7= 2 × k - 3
Zs + Zk = 7= 2 × 5- 3
7 = 7
Nosa
č
je kinemati
č
ki prosto stabilan.
k = 7
Zs = 6
Zk = 4
Zs + Zk = 10= 2 × k - 3
Zs + Zk = 10= 2 × 7- 3
10 < 11
Sistem je unutrašnje kinemati
č
ki labilan.
δ
δ

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
dobiven u presjeku pravaca O
3
– O
23
i O
4
– O
24
. Analogno odre
đ
ivanju pola O
3
pol O
1
dobiven je
presjekom pravaca O
2
– O
12
i pravca oslanjanja plo
č
e I u osloncu 1.
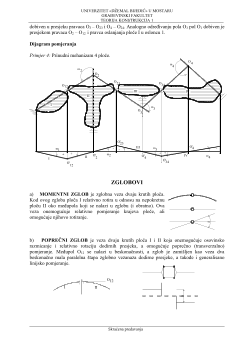
Dijagram pomjeranja
Primjer 4:
Prinudni mehanizam 4 plo
č
e.
-
+
+
-
-
+
+
4
O'
34
O'
4
O'
23
O'
2
O'
12
O'
IV
III
II
I
4
ω
3
ω
2
ω
1
ω
2
3
ω
4
ω
ω
34
O
4
O
3
O
23
O
2
O
12
O
IV
III
II
I
ZGLOBOVI
a)
MOMENTNI ZGLOB
je zglobna veza dvaju krutih plo
č
a.
Kod ovog zgloba plo
č
a I relativno rotira u odnosu na nepokretnu
plo
č
u II oko me
đ
upola koji se nalazi u zglobu (i obratno). Ova
veza onemogu
ć
uje relativno pomjeranje krajeva plo
č
e, ali
omogu
ć
uje njihovo rotiranje.
b)
POPRE
Č
NI ZGLOB
je veza dvaju krutih plo
č
a I i II koja onemogu
ć
uje osovinsko
razmicanje i relativno rotaciju dodirnih presjeka, a omogu
ć
uje popre
č
no (transverzalno)
pomjeranje. Me
đ
upol O
12
se nalazi u beskona
č
nosti, a zglob je zamišljen kao veza dva
beskona
č
no mala paralelna štapa zglobno vezanaza dodirne presjeke, a tako
đ
e i generalisano
linijsko pomjeranje.
I
II
12
δ
δ
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
c)
PODUŽNI ZGLOB
je veza izme
đ
u plo
č
a I i II koja onemogu
ć
uje relativnu rotaciju i
popre
č
no razmicanje dodirnih presjeka, a omogu
ć
uje podužno relativno pomjeranje istih.
Me
đ
upol O
12
nalazi se u beskona
č
nosti na pravcu dodirnih presjeka. Zamišljen je kao veza dva
beskona
č
no mala paralelna štapa u pravcu popre
č
nih dodirnih presjeka.
OSLONCI
a)
POKRETNI OSLONAC
je spoljna veza koja spre
č
ava pomjeranje ta
č
ke oslanjanja, dok
joj dopušta pomjeranje upravno na pravac oslanjanja, a i rotaciju oslonjenog presjeka. To
odre
đ
uje položaj apsolutnog pola oslonjene plo
č
e I koji se nalazi na pravcu oslanjanja.
b)
NEPOKRETNI OSLONAC
je oslonac koji spre
č
ava svako linearno pomjeranje oslonjene
ta
č
ke, a omogu
ć
uje rotaciju iste. To definiše položaj apsolutnog pola oslonjene plo
č
e I koji mora
biti u oslonjenoj ta
č
ki A.
δ

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
α
α
α
cos
2
sin
2
⋅
=
⋅
⋅
=
Ph
ctg
Ph
M
Sli
č
no tome i raspodjeljeno optere
ć
enje pod nagibom
daje pri redukciji na osovinu nosa
č
a dopunske
raspodjeljene spregove intenziteta
m
= g × e × cos
α
Po dužini djelovanja optere
ć
enja mogu biti:
-
stalna: sopstvena težina nosa
č
a i elementi
konstrukcije koji funkcionalno moraju stalno
biti prisutni, te snijeg u podru
č
jima gdje se
pojavljuje,
-
povremena (korisno optere
ć
enje): vjetar, ljudi,
vozila, teret u skladištima, zemljotres itd.
Prema na
č
inu djelovanja dijelimo ih na:
-
nepokretna i
-
pokretna
tako
đ
er i na:
-
direktna i
-
indirektna.
Ra
č
unska optere
ć
enja odre
đ
uju se na bazi stvarnih podataka o nosa
č
u, stalnom optere
ć
enju i
funkciji nosa
č
a, kao i na osnovu važe
ć
ih propisa za odre
đ
ene vrste konstrukcija. Taj dio
stati
č
kog prora
č
una koji prethodi samom iznalaženju sile u popre
č
nim presjecima nosa
č
a
zovemo
ANALIZOM OPTERE
Ć
ENJA.
Prema propisima optere
ć
enja se mogu dijeliti i prema vrstama objekata:
- optere
ć
enje zgrada,
- optere
ć
enje drumskih mostova,
- optere
ć
enje željezni
č
kih mostova itd.
Ili prema zna
č
aju i u
č
estalosti na:
-
glavna,
-
dopunska,
-
naro
č
ita,
a prema uticaju na stvarno stanje napona uslijed eventualnih vibracija dijelimo ih na:
- stati
č
ka i
- dinami
č
ka.
UNUTRAŠNJE SILE
Dejstvo vanjskih sila na nosa
č
izaziva deformaciju istog i pojavu unutrašnjih sila u presjecima
kao rezultante napona.
U otpornosti materijala se govori o naponima, ali moramo naglasiti da se ne može govoriti o
naponima, ako nije ta
č
no definisana ravan (zamišljen presjek nosa
č
a) i ta
č
ka u toj ravni.
Naj
č
eš
ć
e se govori o naponima u ta
č
kama presjeka upravnog na osovinu nosa
č
a na odre
đ
enom
mjestu osovine, ali ne mora uvijek biti tretiranje napona u presjecima upravnim na osovinu ve
ć
i
presjecima pod odre
đ
enim uglom razli
č
itim od 90°. U statici linijskih nosa
č
a smatramo da su
optere
ć
enja i osa nosa
č
a u istoj ravni. Ako tretiramo unutrašnje sile u nekom presjeku nosa
č
a,
izrazi
ć
emo ih preko napona u presjeku upravnom na osovinu, pa
ć
e i naponi biti u ravni nosa
č
a.
g [kN/m']
e
g [kN/m']
h
α
1
2
α
M
1
2
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
(1)
(2)
Presje
č
na sila R i moment poslije redukcije sile R na težište presjeka izraženi su preko napona
formulama (1) i (2).
Sile u presjeku preko komponenata su:
dF
M
dF
T
dF
N
F
xz
F
xz
F
x
∫
∫
∫
=
=
=
σ
τ
σ
Smatramo da nema torzionog momenta M
x
i momenta oko ose z, M
z
.
Šematski prikazano:
M
N
T
T
N
M
T
M
N
N
T
M
M
N
T
T
N
M
M
N
T
T
N
M
POGLED
PO
G
LE
D
POGLED
N
–
normalna sila
– komponenta rezultante unutrašnje sile R u pravcu x – ose (na osovini
nosa
č
a). Pozitivna je kada zateže svoj dio štapa.
T
– transverzalna sila
– komponenta rezultante unutrašnje sile R u pravcu z – ose (normalna na
osovinu nosa
č
a). Pozitivna je kada ima tendenciju da obr
ć
e dio štapa oko drugog kraja u smjeru
kazaljke na satu.
M – momenat savijanja
oko
ose y
, M
y.
Pozitivan je kada izaziva zatezanje donje strane nosa
č
a.
dF
r
p
M
dF
p
R
F
F
∫
∫
=
=
dF
r
p
M
R
z
y
x

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
Ako je
ρ
beskona
č
no dug i ako u gornje jedna
č
ine umjesto
ds
stavimo
dx
onda
ć
emo dobiti
sljede
ć
e jedna
č
ine:
n
dx
dN
−
=
,
,
p
dx
dT
−
=
T
dx
dM
=
, te je
p
dx
M
d
−
=
2
2
x
T
M
x
dx
dM
α
α
α
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
UTICAJNE LINIJE
Op
ć
enito o uticajnim linijama
Pri stati
č
kom ispitivanju jedne konstrukcije odre
đ
uju se izvjesni uticaji, koje vanjsko optere
ć
enje
ili izvjesna sredina vrši na konstrukciju.
Pod tim uticajima podrazumijevamo: reakcije oslonaca, horizontalni potisak luka ili lan
č
anog
nosa
č
a, napadne momente, transverzalne i normalne sile u jednom presjeku, ugibanje pojedinih
ta
č
aka konstrukcije i dr. Sve ove veli
č
ine koje mi ispitujemo, zovemo
uticaji
i obilježavamo ih
sa
Z
.
U slu
č
aju nepokretnih optere
ć
enja uticaje u nosa
č
u tj. u nekom odre
đ
enom presjeku, možemo
odrediti pomo
ć
u ve
ć
poznatih metoda stati
č
kog prora
č
una. Na osnovu dobiveih vrijednosti
unutrašnjih sila možemo na
ć
i ekstremne veli
č
ine momenata i transverzalnih sila. Ali ako na
nos
č
a djeluje pokretno optere
ć
enje, onda se u nosa
č
u ekstremne vrijednosti unutrašnjih sila
pojavljaju u razli
č
itim presjecima nosa
č
a u zavisnosti od kretanja sile.
Da bi lakše odredili vrijednosti uticaja od pokretnog optere
ć
enja koristimo se koncentrisanom
jedini
č
nom silom od 1kN koja se kre
ć
e po nosa
č
u s lijeva na desno ili obrnuto. Udaljenost te
jedini
č
ne sile od jednog oslonca (npr. od oslonca A) se ozna
č
ava sa x, dok je ukupna dužina
nosa
č
a L. Kretanje sile po nosa
č
u izaziva uticaje u svim presjecima nosa
č
a, pa prema tome i za
neki odre
đ
eni presjek možemo da bez ikakvih problema odredimo vrijednosti unutrašnjih sila,
odnosno da nacrtamo uticajnu liniju odre
đ
enog presjeka na nosa
č
u.
Zna
č
i,
uticajna linija
je linija
č
ije ordinate, izmjerene ispod optere
ć
enja, daju veli
č
inu traženog
uticaja od jedini
č
ne sile od 1 kN u presjeku, za koji je ta linija konstruisana. Površian koju
zaklapa uticajna linija sa horizontalom zove se
uticajna površina.
Osobine uticajnih linija
Traženi uticaj od optere
ć
enja na nosa
č
u dobije se pomo
ć
u superpozicije. Uticajne linije crtaju se
samo za jedan odre
đ
eni pravac optere
ć
enja, a mi prou
č
avamo uticajne linije od vertikalnog
optere
ć
enja.
Moramo razlikovati dijagrame unutrašnjih sila nosa
č
a od uticajnih linija, jer se dijagrami
unutrašnjih sila crtaju za neko odre
đ
eno optere
ć
enje, dok se uticajne linije crtaju za neki
odre
đ
eni presjek.
Oblici uticajnih linija
Oblik uticajne linije zavisi od konstrukcije nosa
č
a i od na
č
ina optere
ć
enja, pa prema tome taj
oblik može biti pravolinijski, poligonalni ili krivolinijski. Kod svih stati
č
ki odre
đ
enih nosa
č
a
uticajne linije su prave, dok su kod stati
č
ki neodre
đ
enih nosa
č
a to krive linije drugog ili višeg
stepena. Za slu
č
aj direktnog optere
ć
enja uticajne linije su prave, a za slu
č
aj indirektnog
optere
ć
enja uticajne linije su poligonalne oblika. Ako se sila nalazi u
č
voru onda se uticajna
linija od indirektnog oslanjanja ne razlikuje od uticajne linije direktnog oslanjanja.
Konstruisanje uticajnih linija
Za konstrukciju uticajnih linija postoje dva na
č
ina:
-
stati
č
ki
-
kinemati
č
ki.

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
GERBEROVE GREDE
Greda koja ima
n
oslonaca od kojih je jedan nepokretan, a ostali pokretni i koji su
poredani u jednom pravcu me
đ
usobno povezani štapovima zove se
kontinuirana greda
. Svaka
kontinuirana greda je
n-3
puta stati
č
ki neodre
đ
ena, zbog toga što ima viška reakcija u odnosu na
tri uslova ravnoteže. Umetanjem
n-3
broja zglobova kod kojih je M=0, na kontinuirane grede,
dobivaju se stati
č
ki odre
đ
eni nosa
č
i koji se zovu
Gerberove grede
, po njema
č
kom inženjeru
Heinrich-u Gerber-u (1832.-1912.).
Slika 1: Šeme umetanja zglobova
Prema na
č
inu postavljanja zglobova Gerberove grede se koriste u mostogradnji (b), (c) ili kod
projektovanja rožnja
č
a (d). Pod (e) je još jedan mogu
ć
i slu
č
aj Gerberove grede.
Prilikom umetanja zglobova potrebno je poznavati sljede
ć
a pravila:
1)
u jednom polju ne mogu se umetnuti više od dva zgloba,
2)
u krajnjem polju ne smije postojati više od jednog zgloba i to ne ra
č
unaju
ć
i oslona
č
ki
zglob,
3)
ako u jednom polju postoje dva zgloba, u susjednim poljima smije biti umetnut jedan ili
nijedan,
4)
ako u krajnjem polju postoji jedan zglob, onda u sljede
ć
em polju može biti umetnut samo
jedan,
5)
izme
đ
u dva zgloba mogu biti najviše dva oslonca.
Poštuju
ć
i pravila umetanja zglobova dobija se niz prostih greda i greda sa propustima. Na slici 2
može se vidjeti na
č
in rastavljanja nosa
č
a u zglobovima i na taj na
č
in dobija se
šema
rastavljanja nosa
č
a
. Dijelovi grede koji imaju dva stvarna oslonca, odnosno oni dijelovi koji se
mogu prora
č
unati sami za sebe zovemo
primarnim nosa
č
ima
, a dijelovi nosa
č
a koji imaju
jedan stvarni i jedan oslonac dobiven rastavljanjem nosa
č
a u zglobu ili dva oslonca dobivena
rastavljanjem nosa
č
a u dva susjedna zgloba zovemo
sekundarnim nosa
č
ima
. Primarni dijelovi
nosa
č
a idu „dolje“, a sekundarni „gore“. Prilikom rastavljanja nosa
č
a u zglobovima pojavljuju se
dvije reakcije, vertikalna i horizontalna. U slu
č
aju da na cijelom nosa
č
u ne postoji horizontalno
vanjsko optre
ć
enje, onda
ć
e i horizontalne reakcije u zglobovima biti jednake nuli, u protivnom
horizontalna reakcija
ć
e se pojaviti na mjestima gdje postoji vanjsko horizontalno optere
ć
enje.
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
Slika 2: Na
č
in rastavljanja Gerberovih greda u zglobovima
DEFINISANJE MJESTA ZGLOBOVA
Kod odre
đ
ivanja mjesta zglobova pored ve
ć
spomenutih pravila umetanja, moramo paziti
i na ta
č
nu udaljenost zgloba od oslonca. Da bi definisali tu udaljenost u razmatranje
ć
e biti uzeta
jedna rožnja
č
a nekog hangara kod koje su sve dužine me
đ
u osloncima jednake, a maksimalni i
minimalni momenti savijanja su isti i to
16
2
ql
za slu
č
aj stalnog optere
ć
enja-kontinuirano
optere
ć
enje (snijeg, vlastita težina). Da bi postavili zglob na gredi, onda treba paziti gdje je
momenat savijanja jednak nuli i jedino je tu mogu
ć
e postaviti zglob, te je to mjesto
najekonomi
č
nije mjesto za položaj zgloba na nosa
č
u.
Slika 3: Upore
đ
enje dijagrama momenata savijanja proste grede i Gerberove grede
Najekonomi
č
nija mjesta na nosa
č
u su mjesta gdje se mijenja predznak momenta savijanja, a što
se može vidjeti na slici 3. Prvo se nacrta dijagram momenata savijanja za svaki štap Gerberove
grede posebno, kao za prostu gredu za pozitivnu površinu. Potom se ucrtaju svi negativni

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
2
'
'
16
7
)
'
(
1
1
1
x
q
x
l
q
x
M
⋅
−
⋅
⋅
⋅
=
Pošto je mjesto gdje se nalazi zglob i moment savijanja je jednak nuli, onda se dobiva:
0
)
'
(
1
=
x
M
l
l
x
⋅
=
⋅
=
875
,
0
8
7
'
1
Vrijednost maksimalnog momenta savijanja kao što se može vidjeti na slici 5 je:
2
2
2
16
532
,
1
2
16
7
2
.
max
l
q
q
l
q
q
E
M
V
⋅
⋅
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
=
⋅
=
Ako na ovaj na
č
in odredimo mjesta zglobova dobi
ć
e se najekonomi
č
niji sistem, jer
ć
e se u ovom
slu
č
aju mo
ć
i koristiti najmanji mogu
ć
i presjeci dobiveni prora
č
unom.
UTICAJNE LINIJE KOD GERBEROVIH GREDA
Odre
đ
ivanje uticajnih linija kod Gerberovih greda može se uraditi analiti
č
kim
kinemati
č
kim i grafi
č
kim na
č
inom. Da bi mogli odrediti uticajne linije, bilo kojim na
č
inom,
moraju se poštovati sljede
ć
a pravila:
1)
definisati kretanje jedini
č
ne sile po nosa
č
u,
2)
nacrtati šemu rastavljanja nosa
č
a,
3)
odrediti uticajne linije za dijelove nosa
č
a na kojima se nalazi presjek, bili oni primarni ili
sekundarni,
4)
produžiti uticajne linije kroz oslonce do zglobova gdje se „lome“ i do kraja nosa
č
a,
5)
vrijednost uticajnih linija za momente, transverzalne i normalne sile je jednaka nuli u
osloncima, dok u zgloovima postoje vrijednosti, jer se u zglobovima uticajne linije
„lome“,
6)
vrijednost uticajnih linija za traženu reakciju je jednaka 1,0, a u ostalim osloncima je
jednaka nuli, dok u zlobovima postoje vrijednosti,
7)
uticajna linija se završava ukoliko je (slika 6):
a.
kraj grede,
b.
ako su dva oslonca u polju,
c.
ako se presjek nalazi na sekundarnom nosa
č
u, koji je prosta greda, te zbog toga se
uticajna linija ne može produžiti do zgloba ili kroz susjedni oslonac,
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
Slika 6: Uticajne linije za razne presjeke kod Gerberovih greda

UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
PRORA
Č
UN UNUTRAŠNJIH SILA
Teorema 1
Dosadašnji na
č
in prora
č
una unutrašnjih sila je baziran na teoremi 1.
Teorema 2
Ova teorema je bazirana na prora
č
unu unutrašnjih sila koje se nalaze izme
đ
u dva ve
ć
prora
č
unata presjeka na krajevima optere
ć
enja.
Ako su nam poznati momenti savijanja
M
n-1
i
M
n
u presjecima na nosa
č
u
n-1
i
n
kao što je dato
na slici 1.
Slika 1
Vrijednost momenta savijanja na udaljenosti
x
od presjeka
n-1
iznosi:
x
n
n
x
m
x
T
M
M
+
⋅
+
=
−
−
1
1
m
x
je ovdje vrijednost momenta savijanja izme
đ
u presjeka
n-1
i presjeka
x
.
Ako u gornju jedna
č
inu unesemo
x=l
onda je:
n
n
n
n
m
l
T
M
M
+
⋅
+
=
−
−
1
1
a ako gornju jedna
č
inu pomnožimo sa
x/l
dobivamo:
x
n
n
n
x
m
l
x
m
l
x
l
M
l
x
M
M
+
⋅
−
−
⋅
+
⋅
=
−
1
Na ovaj na
č
in se može prora
č
unati vrijednost parabole izme
đ
u dva krajnja presjeka kao što se
može vidjeti na Slici 2.
UNIVERZITET «DŽEMAL BIJEDI
Ć
» U MOSTARU
GRA
Đ
EVINSKI FAKULTET
TEORIJA KONSTRUKCIJA 1
Skra
ć
ena predavanja
Slika 2
Ako su predzanci momenata savijanja jednaki onda se sabiraju, dok se u suprotnom slu
č
aju
oduzimaju, kao što se može vidjeti na slici 3.
Slika 3
Da bi se odredio maksimalni
momenat savijanja, prvo se mora
odrediti mjesto, gdje je vrijednost
transverzalnih sila jednaka nuli,
kao što se može vidjeti na slici 4.
Slika
4

Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































