1
S
v
e
u
č
i
l
i
š
t
e
u
Za
g
r
e
b
u
Filozofski fakultet
Pr
o
f
.
d
r
.
s
c
.
Bo
ž
i
d
a
r
Te
pe
š
SKRIPTE IZ STATISTIKE
U Zagrebu 2000.
Svako kopiranje i prepisivanje bez dozvole autora nije dozvoljeno
2
Sa
dr
ž
a
j
1.
Vi
š
e
d
i
me
n
z
i
o
n
a
l
n
a
s
l
u
č
a
j
n
a
v
a
rijabla
3
2.
Sl
u
č
a
j
n
i
u
z
o
r
a
k
i
s
t
a
t
i
s
t
i
k
a
8
3.
Ocjena parametara razdiobe
10
4.
Te
s
t
i
r
a
n
j
e
s
t
a
t
i
s
t
i
č
k
i
h
h
i
p
o
t
e
z
a
12
5.
Linearna regresija
22
6.
Pitanja
28
7.
Test iz vjerojatnosti
29
4
i
j
x
j
i
j
2
y
j
i
i
1
)
y
,
x
(
f
)
y
(
f
)
y
,
x
(
f
)
x
(
f
U
n
a
š
e
m
s
l
u
č
a
j
u
f
1
(x
i
) i f
2
(y
j
) jesu:
x
i
ili y
j
0
1
2
f
1
(x
i
)
0.25
0.50
0.25
f
2
(y
j
)
0.49
0.42
0.09
F
u
n
k
c
i
j
e
v
j
e
r
o
j
a
t
n
o
s
t
i
ma
r
g
i
n
a
l
n
e
r
a
z
d
i
o
b
e
mo
g
u
s
e
i
z
r
a
č
u
n
a
t
i
z
b
r
a
j
a
n
j
e
m
v
r
i
j
e
d
n
o
s
t
i
p
o
stupcima ili redcima tablice funkcije vjerojatnosti dvodimenzionalne razdiobe i napisati
na marginama tablice. U n
a
š
e
m
s
l
u
č
a
j
u
t
o
j
e
s
t
:
x
i
y
j
0
1
2
f
1
(x
i
)
0
0.04
0.12
0.09
0.25
1
0.20
0.30
0
0.50
2
0.25
0
0
0.25
f
2
(y
j
)
0.49
0.42
0.09
1
Za
s
v
a
k
u
d
v
o
d
i
me
n
z
i
o
n
a
l
n
u
r
a
z
d
i
o
b
u
mo
ž
e
mo
i
z
r
a
č
u
n
a
t
i
n
i
z
u
v
j
e
t
n
i
h
r
a
z
d
i
o
b
i
s
funkcijama vjerojatnosti f(x
i
|y
j
) i f(y
j
|x
i
) uv
j
e
t
n
i
h
s
l
u
č
a
j
n
i
h
v
a
r
i
j
a
b
l
i
(
X|
Y=y
j
) i (Y|X=x
i
)
koje jesu:
)
x
(
f
)
y
,
x
(
f
i
j
)
y
(
f
)
y
,
x
(
f
j
i
i
1
j
i
j
2
j
i
)
x
|
y
(
f
)
y
|
x
(
f
U
n
a
š
e
m
s
l
u
č
a
j
u
d
v
o
d
i
me
n
z
i
o
n
a
l
n
e
b
i
n
o
mn
e
r
a
z
d
i
o
b
e
B(
2
,
0
.
5
,
0
.
3
)
f
u
n
k
c
i
j
e
v
j
e
r
o
j
a
t
n
o
s
t
i
u
v
j
e
t
n
i
h
s
l
u
č
a
j
n
i
h
v
a
r
i
j
a
b
l
i
j
e
s
u
:
x
i
0
1
2
f(x
i
|0)
0.0816
0.4082
0.5102
f(x
i
|1)
0.2857
0.7143
0
f(x
i
|2)
1
0
0
y
j
0
1
2
f(y
j
|0)
0.16
0.48
0.36
f(y
j
|1)
0.4
0.6
0
f(y
j
|2)
1
0
0
Za
s
v
a
k
u
u
v
j
e
t
n
u
s
l
u
č
a
j
n
u
v
a
r
i
j
a
b
l
u
mo
ž
e
mo
i
z
r
a
č
u
n
a
t
i
o
č
e
k
i
v
a
n
j
e
E(
X|
Y=y
j
), E(Y|X=x
i
)
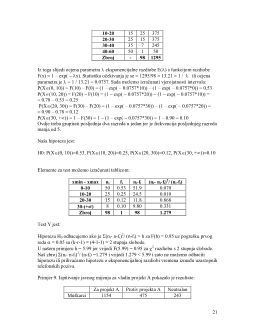
kaja jesu E(X|Y=0)=1.4286, E(X|Y=1)=0.7143, E(X|Y=2)=0, E(Y|X=0)=1.2,
E(Y|X=1)=0.6 i E(Y|X=2)=0.
5
Gr
a
f
i
č
k
i
s
e
s
p
a
j
a
n
j
e
m
E(
X|
Y=y
j
) i E(Y|X=x
i
) dobivaju krivulje regresije X|Y i Y|X koje
s
e
mo
g
u
p
r
i
k
a
z
a
t
i
g
r
a
f
i
č
k
i
:
Y|X
X|Y
Krivulje regresije
X
Y
0.0
0.5
1.0
1.5
2.0
2.5
3.0
0.0
0.5
1.0
1.5
2.0
2.5
3.0
Iz grafa regresijskih krivulja je vidljiva njihova razlika. Tu razliku mož
e
mo
n
u
me
r
i
č
k
i
izraziti kovarijancom i koeficijentom korelacije. Kovarijanca cov(X, Y) jest:
)
Y
(
E
)
X
(
E
)
XY
(
E
)))
Y
(
E
Y
))(
X
(
E
X
((
E
)
Y
,
X
cov(
p
r
i
č
e
mu
s
u
E(
X)
i
E(
Y)
o
č
e
k
i
v
a
n
j
a
ma
r
g
i
n
a
l
n
i
h
r
a
z
d
i
o
b
a
,
a
(
X-E(X))(Y-E(Y)) i XY su
s
l
u
č
a
j
n
e
v
a
r
i
j
a
b
l
e
d
o
b
i
v
e
n
e
i
z
d
v
o
d
i
me
n
z
i
o
n
a
l
n
e
s
l
u
č
a
jne varijable (X, Y). Koeficijent
korelacije
(X, Y) jest:
)
Y
(
V
)
X
(
V
)
Y
,
X
cov(
)
Y
,
X
(
U
n
a
š
e
m
p
r
i
mj
e
r
u
k
o
v
a
r
i
j
a
n
c
a
i
k
o
e
f
i
c
i
j
e
n
t
k
o
r
e
l
a
c
i
j
e
j
e
s
u
:
E(X) = 0*0.25+1*0.5+2*0.25 = 1
E(Y) = 0*0.49+1*0.42+2*0.09 = 0.6
V(X) = 0
2
*0.25+1
2
*0.5+2
2
*0.25-1
2
= 0.5
V(Y) = 0
2
*0.49+1
2
*0.42+2
2
*0.09-0.6
2
= 0.42
cov(X, Y) = (0-1)(0-0.6)0.04+(0–
1)(1-0.6)0.12+(0-1)(2-0.6)0.09+(1-1)(0-0.6)0.20+
+(1-1)(1-0.6)0.30+(1-1)(2-0.6)0+(2-1)(0-0.6)0.25+(2-1)(1-0.6)0+(2-1)(2-0.6)0 =
= 0*0.7+1*0.3+2*0+4*0-1*0.6 = -0.3
(X, Y) = -0.6547
7
c)
F
u
n
k
c
i
j
e
v
j
e
r
o
j
a
t
n
o
s
t
i
u
v
j
e
t
n
i
h
s
l
u
č
a
j
n
i
h
v
a
r
i
j
a
b
l
i
s
u
:
x
1
0
1
2
f(x
1
|0)
2/7
4/7
1/7
f(x
1
|1)
10/21
10/21
1/21
f(x
1
|2)
5/7
2/7
0
f(x
1
|3)
1
0
0
x
2
0
1
2
3
f(x
2
|0)
5/28
15/28
15/56
1/56
f(x
2
|1)
5/14
15/28
3/28
0
f(x
2
|2)
5/8
3/8
0
0
d)
Oč
e
k
i
v
a
n
j
a
u
v
j
e
t
n
i
h
s
l
u
č
a
j
n
i
h
v
a
r
i
j
a
b
l
i
s
u
:
8
3
8
3
4
3
28
3
28
15
8
9
56
1
56
15
28
15
1
7
2
7
2
1
7
4
21
1
21
10
1
7
6
7
1
7
4
1
1
)
2
|
2
X
(
E
,
2
1
)
1
|
2
X
(
E
,
3
2
1
)
0
|
2
X
(
E
,
0
)
3
|
X
(
E
,
1
)
2
|
X
(
E
,
2
1
)
1
|
X
(
E
,
2
1
)
0
|
X
(
E
Regresijske krivulje jesu:
E(X1/X2)
E(X2/X1)
Krivulje regresije
X1
X2
0.0
0.5
1.0
1.5
2.0
2.5
3.0
0.0
0.5
1.0
1.5
2.0
e)
Kovarijanca i koeficijent korelacije jesu:
