
Termodinamika i termotehnika
SVEU
Č
ILIŠTE U SPLITU
KEMIJSKO-TEHNOLOŠKI FAKULTET
ZAVOD ZA TERMODINAMIKU
TERMODINAMIKA I TERMOTEHNIKA
(Priru
č
nik – formule i tablice)
dr. sc. Vanja Martinac, red. prof.
Split, ak. god. 2008./2009.
Predgovor
Priru
č
nik “TERMODINAMIKA I TERMOTEHNIKA” sadrži uz kra
ć
e teorijske
izvode formule i tablice koji
ć
e njegovim korisnicima omogu
ć
iti lakše savladavanje
nastavne gra
ñ
e i obradu nastavnih sadržaja pri rješavanje numeri
č
kih primjera iz ove
znanstvene discipline.
Svako rješavanje zadataka podrazumijeva korištenje razli
č
itih literaturnih izvora i
broj
č
anih podataka.
Stoga je ovaj priru
č
nik prvenstveno osmišljen i namijenjen studentima za korištenje na
pismenom dijelu ispita iz termodinamike.
Zahvaljujem se profesorima dr. sc. Nedjeljki Petric i dr. sc. Nenadu Kuzmani
ć
u na
izvršenoj recenziji.
U Splitu, 15.07.2008.
Prof. dr. sc. Vanja Martinac

str.
16.1.1.
Provo
ñ
enje topline kroz ravnu stijenku ………………………………...
40.
16.1.2.
Provo
ñ
enje topline kroz višeslojnu ravnu stijenku ……………………..
41.
16.1.2.1. Okomiti i/ili horizontalni smještaj vodi
č
a ili izolatora ……….
43.
16.1.3.
Provo
ñ
enje topline kroz cilindri
č
nu (cijevnu) stijenku ………………...
47.
16.2.
Prijenos topline miješanjem (vrtloženjem) ili konvekcija …………………………..
49.
16.3.
Prolaz topline ………………………………………………………………………..
51.
16.4.
Izmijenjiva
č
i topline …………………………………………………………………
56.
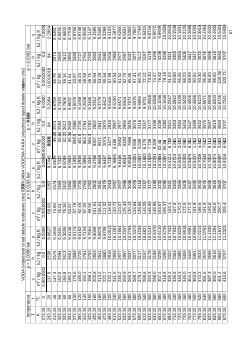
17. TABLICE ZA VODENU PARU ………………………………………………………………
58.
- VRELA VODA I ZASI
Ć
ENA VODENA PARA (S PROMJENOM TLAKA) ……………..
58.
- VRELA VODA I ZASI
Ć
ENA VODENA PARA (S PROMJENOM TEMPERATURE) …... 63.
- VODA I PREGRIJANA VODENA PARA …………………………………………………..
67.
- VODENA PARA U NADKRITI
Č
NOM PODRU
Č
JU ...…………………………………….
87.
18. TABLICE ZA RASHLADNA SREDSTVA …...……………………………………………… 89.
- ZASI
Ć
ENA PARA AMONIJAKA …………………………………………………………... 89.
- ZASI
Ć
ENA PARA METIL KLORIDA ……………………………………………………...
90.
- ZASI
Ć
ENA PARA METILEN KLORIDA ………………………………………………….
91.
- ZASI
Ć
ENA PARA FREONA 12 …………………………………………………………….
92.
- ZASI
Ć
ENA PARA UGLJI
Č
NOG DIOKSIDA ……………………………………………… 93.
- ZASI
Ć
ENA PARA SUMPORNOG DIOKSIDA …………………………………………….
94.
19. LITERATURA …………………………………………………………………………………
95.
FORMULE ZA PRVI PARCIJALNI KOLOKVIJ
1
1.
OSNOVNE TERMODINAMI
Č
KE VELI
Č
INE STANJA
Specifi
č
ni volumen, v je volumen kojeg zauzima jedinica mase tvari.
m
V
v
=
v
= specifi
č
ni volumen, m
3
kg
–1
V
= ukupni volumen, m
3
m
= masa tvari, kg
Recipro
č
na vrijednost specifi
č
nog volumena je gusto
ć
a tvari:
V
m
v
=
=
1
ρ
, kg m
–3
.
Tlak, p je sila koja djeluje okomito na jedinicu površine.
A
F
p
=
, N m
–2
.
Razlikujemo apsolutni tlak, nadtlak i sniženi tlak ili podtlak (vakuum). Nadtlak i sniženi tlak odnose
se na atmosferski tlak, dok je apsolutni tlak ukupni tlak kojim djeluje plin ili para. Apsolutni tlak predstavlja
zbroj barometarskog i manometarskog tlaka, tj.
m
b
a
p
p
p
+
=
Ako je tlak u nekoj posudi manji od barometarskog, taj podtlak ili vakuum o
č
itava se na vakuummetru. U
tom slu
č
aju apsolutni tlak je jednak razlici barometarskog tlaka i vrijednosti koju pokazuje vakuummetar, tj.
v
b
a
p
p
p
−
=
Treba napomenuti da samo apsolutni tlak predstavlja veli
č
inu stanja.
Temperatura,
T
je termi
č
ka veli
č
ina stanja koja ozna
č
uje mjeru srednje kineti
č
ke energije molekula.
2.
JEDNADŽBA STANJA IDEALNOG PLINA
Veli
č
ine stanja, tj.
p
,
v
i
T
, me
ñ
usobno su ovisne. Najprikladnije izražavanje ovisnosti me
ñ
u osnovnim
parametrima stanja predstavlja analiti
č
ka jednadžba koja ima oblik:
f
(
p
,
v
,
T
) = 0.
Prema tome, ako su poznate dvije od ovih veli
č
ina, tre
ć
a se može izra
č
unati iz odnosa:
( )
T
v
f
p
,
1
=
,
( )
T
p
f
v
,
2
=
,
( )
v
p
f
T
,
3
=
.
FORMULE ZA PRVI PARCIJALNI KOLOKVIJ
3
Prema mjerenjima, svi jednoatomni plinovi imaju jednake toplinske kapacitete koji su neovisni o
temperaturi, a iznose
( )
1
1
plin
i
jednoatomn
,
K
kmol
kJ
20.93
−
−
m
p
C
.
Kod dvoatomnih plinova, molarni toplinski kapaciteti su tako
ñ
er gotovo jednaki za razli
č
ite plinove, ali nisu
neovisni o temperaturi. Kod srednjih temperatura za dvoatomne plinove
( )
1
1
plin
dvoatomni
,
K
kmol
kJ
29.31
−
−
m
p
C
.
Kod višeatomnih plinova ove su vrijednosti još ve
ć
e, ali toplinski kapaciteti razli
č
itih plinova s istim brojem
atoma nisu više me
ñ
usobno jednaki.
Pored razlike, posebno je zna
č
ajan i omjer toplinskih kapaciteta koji obilježavamo s
κ
,
v
p
v
p
C
C
c
c
=
=
κ
.
Kod jednoatomnih plinova
κ
= 1.667.
Kod dvoatomnih plinova
κ
= 1.4.
6. SMJESE PLINOVA
Volumni udjeli:
itd.
,
2
2
1
1
V
V
V
V
=
=
ϕ
ϕ
1
...
2
1
=
+
+
+
ϕ
ϕ
ϕ
.
Maseni udjeli:
itd.
,
2
2
1
1
m
m
m
m
=
=
ω
ω
1
...
3
2
1
=
+
+
+
+
n
ω
ω
ω
ω
.
Kod istih temperatura i tlakova, mase pojedinih komponenata proporcionalne su volumenima i
molarnim masama, stoga možemo napisati:
2
2
1
1
2
1
2
2
1
1
2
1
2
2
1
1
2
1
ili
M
M
M
V
V
M
V
V
m
m
m
m
M
V
M
V
m
m
ϕ
ϕ
ω
ω
=
=
⇒
=
Kod ve
ć
eg broja komponenata to izražavamo omjerom:
n
n
n
M
M
M
ϕ
ϕ
ϕ
ω
ω
ω
:
...
:
:
:
...
:
:
2
2
1
1
2
1
=
ili za i-ti plin
(
)
∑
=
=
n
i
i
i
i
i
i
M
M
1
ϕ
ϕ
ω
jer je
1
1
=
∑
=
n
i
i
ω
.
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































