
Furijeova analiza
Sadrˇ
zaj
1 Unitarni prostori
3
1.1 Motivacija . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.2 Definicija skalarnog produkta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1.3 Prostori
L
2
i
l
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.3.1
Definicije . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
1.3.2
Konvergencija u
L
2
i uniformna konvergencija . . . . . . . . . . . . . . . . .
9
1.4 Schwarzova nejednakost. Nejednakost trokuta . . . . . . . . . . . . . . . . . . . . .
10
1.5 Ortogonalnost . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.5.1
Definicije i primjeri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
1.5.2
Ortogonalne projekcije . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
1.5.3
Gramm-Schmidtov postupak ortogonalizacije . . . . . . . . . . . . . . . . .
18
1.6 Linearni operatori. Adjungirani operator . . . . . . . . . . . . . . . . . . . . . . . .
19
1.6.1
Linearni operatori . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.6.2
Adjungirani operator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
2 Fourierovi redovi
23
2.1 Uvod . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.1.1
Povijest . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.1.2
Signalna analiza . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
23
2.1.3
Parcijalne diferencijalne jednadˇzbe . . . . . . . . . . . . . . . . . . . . . . .
24
2.2 Raˇcunanje Fourierovih redova . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.2.1
Interval
−
π
≤
x
≤
π
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
25
2.2.2
Op´ceniti intervali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
2.2.3
Fourierov red parnih i neparnih funkcija . . . . . . . . . . . . . . . . . . . .
29
2.2.4
Primjeri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
2.2.5
Kompleksni oblik Fourierovog reda . . . . . . . . . . . . . . . . . . . . . . .
38
2.3 Teoremi o konvergenciji Fourierovih redova . . . . . . . . . . . . . . . . . . . . . .
42
2.3.1
Riemann-Lebesgueova lema . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
2.3.2
Konvergencija u toˇcki neprekinutosti . . . . . . . . . . . . . . . . . . . . . .
43
2.3.3
Konvergencija u toˇcki prekida . . . . . . . . . . . . . . . . . . . . . . . . . .
46
2.3.4
Uniformna konvergencija . . . . . . . . . . . . . . . . . . . . . . . . . . . .
50
2.3.5
Konvergencija u srednjem . . . . . . . . . . . . . . . . . . . . . . . . . . . .
52
3 Fourierova transformacija
60
3.1 Fourierova transformacija . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
3.1.1
Fourierova integralna formula . . . . . . . . . . . . . . . . . . . . . . . . . .
60
3.1.2
Primjeri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
62
3.2 Svojstva Fourierove transformacije . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
1
SADRˇ
ZAJ
3.2.1
Osnovna svojstva . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
3.2.2
Fourierova transformacija konvolucije . . . . . . . . . . . . . . . . . . . . .
71
3.2.3
Adjungirani operator Fourierove transformacije . . . . . . . . . . . . . . . .
72
3.2.4
Plancherelova formula . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
3.3 Linearni filteri . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
3.3.1
Vremenski invarijantni filteri . . . . . . . . . . . . . . . . . . . . . . . . . .
73
3.3.2
Uzroˇcnost i konstrukcija filtera . . . . . . . . . . . . . . . . . . . . . . . . .
76
3.4 Teorem uzorkovanja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
80
3.5 Princip neodredenosti . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83
4 Diskretna Fourierova analiza
87
4.1 Diskretna Fourierova transformacija . . . . . . . . . . . . . . . . . . . . . . . . . .
87
4.1.1
Definicija diskretne Fourierove transformacije . . . . . . . . . . . . . . . . .
88
4.1.2
Svojstva diskretne Fourierove transformacije . . . . . . . . . . . . . . . . . .
89
4.1.3
Brza Fourierova transformacija . . . . . . . . . . . . . . . . . . . . . . . . .
91
4.1.4
Aproksimacija Fourierove transformacije pomo´cu brze Fourierove transfor-
macije . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
4.1.5
Primjena – identifikacija parametara . . . . . . . . . . . . . . . . . . . . . .
96
4.1.6
Primjena – diskretizacija obiˇcne diferencijalne jednadˇzbe . . . . . . . . . . .
97
4.2 Diskretni signali . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
98
4.2.1
Vremenski invarijantni, diskretni linearni filteri . . . . . . . . . . . . . . . .
98
5 Haarova valna analiza
100
5.1 Zaˇsto vali´ci? . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
5.2 Haarovi vali´ci . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
5.2.1
Haarova step funkcija . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101
5.2.2
Osnovna svojstva Haarove step funkcije . . . . . . . . . . . . . . . . . . . . 102
5.2.3
Haarov vali´c . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
5.3 Haarovi algoritmi dekompozicije i rekonstrukcije . . . . . . . . . . . . . . . . . . . 108
5.3.1
Dekompozicija . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
5.3.2
Rekonstrukcija . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
5.3.3
Filteri i dijagrami . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 119
5.4 Saˇzetak . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 120
Dodatak – procedure u Matlabu
122
A Op´cenita procedura saˇzimanja . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
B Primjena FFT procedure za filtriranje i saˇzimanje . . . . . . . . . . . . . . . . . . . 122
C Procedure za saˇzimanje i filtriranje vali´ca . . . . . . . . . . . . . . . . . . . . . . . . 123
2
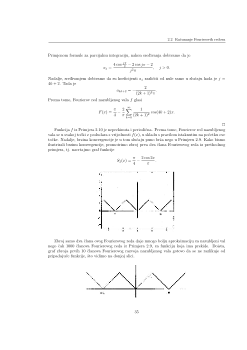
UNITARNI PROSTORI
Skalarni produkti imaju mnoga zanimljiva svojstva. Na primjer, skalarni produkt je bilinearno
preslikavanje, odnosno vrijedi
h
x
+
y
,
z
i
=
h
x
,
z
i
+
h
y
,
z
i
i
h
x
,
y
+
z
i
=
h
x
,
y
i
+
h
x
,
z
i
.
Ostala svojstva koja zadovoljavaju prethodno definirani skalarni produkti, popisani su kao aksiomi
u sljede´coj definiciji. Provjerite da definirani skalarni produkti u
R
n
i
C
n
zadovoljavaju te aksiome.
Definicija 1.1.
Skalarni produkt na kompleksnom vektorskom prostoru
V
je funkcija
h·
,
·i
:
V
×
V
→
C
koja zadovoljava sljede´ca svojstva
•
pozitivnost:
h
v
,
v
i
>
0
za svaki vektor
v
∈
V
, razliˇcit od nulvektora,
•
konjugirana simetriˇcnost:
h
v
,
w
i
=
h
w
,
v
i
, za bilo koje vektore
v
,
w
∈
V
,
•
homogenost:
h
c
v
,
w
i
=
c
h
v
,
w
i
, za bilo koje vektore
v
,
w
∈
V
i skalar
c
∈
C
,
•
aditivnost:
h
u
+
v
,
w
i
=
h
u
,
w
i
+
h
v
,
w
i
za bilo koje vektore
u
,
v
,
w
∈
V
.
Vektorski prostor na kojemu je definiran skalarni produkt naziva se unitarni prostor.
Kako bismo istaknuli pripadaju´ci vektorski prostor
V
, ponekad ´cemo skalarni produkt oznaˇcavati
kao
h
,
i
V
.
Pomo´cu prethodne definicije takoder moˇzemo definirati realni skalarni produkt na realnom
vektorskom prostoru, pri ˇcemu je skalar
c
u svojstvu homogenosti realan, a svojstvo konjugirane
simetriˇcnosti prelazi u svojstvo simetriˇcnosti tj.
h
v
,
w
i
=
h
w
,
v
i
.
Uoˇcimo kako drugo i ˇcetvrto svojstvo povlaˇce aditivnost u drugom faktoru:
h
u
,
v
+
w
i
=
h
u
,
v
i
+
h
u
,
w
i
. Drugo i tre´ce svojstvo povlaˇce da skalar izluˇcen iz drugog faktora dolazi konjugiran
ispred skalarnog produkta:
h
v
, c
w
i
=
h
c
w
,
v
i
=
c
h
w
,
v
i
=
c
h
v
,
w
i
.
Svojstvo pozitivnosti povlaˇci da svakom vektoru moˇzemo pridruˇziti nenegativan broj
||
v
||
=
p
h
v
,
v
i
kojeg nazivamo duljina ili norma vektora
v
. Pomo´cu duljine moˇzemo definirati i udaljenost
dvaju vektora u prostoru
V
:
udaljenost vektora
v
i
w
=
||
v
−
w
||
.
Uoˇcimo kako svojstvo pozitivnosti skalarnog produkta povlaˇci da je
||
v
−
w
||
= 0 ako i samo ako
je
v
=
w
. Pojam udaljenosti omogu´cava definiciju konvergencije niza vektora (
v
k
)
k
∈
N
. Naime,
v
k
→
v
ako
||
v
k
−
v
|| →
0
.
Rijeˇcima,
v
k
teˇzi ka
v
ako udaljenost izmedu
v
k
i
v
teˇzi k nuli kada
k
raste prema beskonaˇcnosti.
Pogledajmo neke primjere skalarnih produkata.
Primjer 1.2.
Neka je
P
n
vektorski prostor polinoma stupnja
≤
n
, s kompleksnim koeficijentima.
Ako je
p
=
P
n
j
=0
a
j
x
j
i
q
=
P
n
j
=0
b
j
x
j
, dokaˇzimo da je
h
p, q
i
=
n
X
j
=0
a
j
b
j
skalarni produkt na prostoru
P
n
.
4
1.2 Definicija skalarnog produkta
Rjeˇsenje:
Moramo provjeriti aksiome iz definicije skalarnog produkta. Imamo da je
h
p, p
i
=
n
X
j
=0
a
j
a
j
=
n
X
j
=0
|
a
j
|
2
≥
0
.
Kako je apsolutna vrijednost uvijek nenegativna, slijedi da je
h
p, p
i
= 0 ako i samo ako je
a
1
=
a
2
=
. . .
=
a
n
= 0, odnosno ako je
p
= 0, pa slijedi pozitivnost.
Nadalje, zbog svojstava operacije konjugiranja vrijedi
h
p, q
i
=
n
X
j
=0
a
j
b
j
=
n
X
j
=0
b
j
a
j
=
h
q, p
i
,
pa slijedi konjugirana simetriˇcnost.
Dokaˇzimo, sada, svojstvo homogenosti. Naime, kako je
cp
=
P
n
j
=0
ca
j
x
j
, slijedi da je
h
cp, q
i
=
n
X
j
=0
ca
j
b
j
=
c
n
X
j
=0
a
j
b
j
=
c
h
p, q
i
.
Konaˇcno, ako je
r
=
P
n
j
=0
c
j
x
j
imamo da je
h
p
+
q, r
i
=
n
X
j
=0
(
a
j
+
b
j
)
c
j
=
n
X
j
=0
a
j
c
j
+
n
X
j
=0
b
j
c
j
=
h
p, r
i
+
h
q, r
i
,
odakle slijedi aditivnost, ˇcime je tvrdnja dokazana.
¤
Uoˇcimo da u prethodnom primjeru skalarni produkt moˇzemo identificirati sa standardnim
skalarnim produktom u
C
n
+1
, pri ˇcemu toˇcku (
a
0
, a
1
, . . . , a
n
) identificiramo s polinomom
p
=
P
n
j
=0
a
j
x
j
.
Na istom vektorskom prostoru moˇzemo definirati razliˇcite skalarne produkte. Pogledajmo
sljede´ci primjer.
Primjer 1.3.
Neka su
v
= (
v
1
, v
2
)
i
w
= (
w
1
, w
2
)
vektori u
C
2
. Dokaˇzimo da je relacijom
h
v
,
w
i
= (
w
1
, w
2
)
µ
2
−
i
i
3
¶ µ
v
1
v
2
¶
,
definiran skalarni produkt u
C
2
, uz standardno mnoˇzenje matrica.
Rjeˇsenje:
Pomnoˇzimo prvo matrice u gornjoj definiciji. Imamo da je
h
v
,
w
i
= (
w
1
, w
2
)
µ
2
−
i
i
3
¶ µ
v
1
v
2
¶
= (
w
1
, w
2
)
µ
2
v
1
−
iv
2
iv
1
+ 3
v
2
¶
= 2
v
1
w
1
−
iv
2
w
1
+
iv
1
w
2
+ 3
v
2
w
2
.
Sada provjeravamo aksiome. Najteˇze je pokazati svojstvo pozitivnosti. Imamo da je
h
v
,
v
i
= 2
v
1
v
1
−
iv
2
v
1
+
iv
1
v
2
+ 3
v
2
v
2
= 2
|
v
1
|
2
+ 3
|
v
2
|
2
+
i
(
v
1
v
2
−
v
2
v
1
)
.
5

1.3 Prostori
L
2
i
l
2
skup vektora je linearno nezavisan ako i samo ako je svaki njegov konaˇcan podskup linearno neza-
visan. Uoˇcimo kako, na primjer, funkcija
f
(
t
) =
1
t
ne pripada prostoru
L
2
([0
,
1]) zato jer je
R
1
0
¡
1
t
¢
2
dt
=
∞
.
Skalarni produkt na
L
2
.
Obratimo sada pozornost na konstrukciju skalarnog produkta na
prostoru
L
2
. Kako bismo dobili ideju za konstrukciju skalarnog produkta na
L
2
prvo ´cemo
”diskretizirati” interval [
a, b
]. Zbog jednostavnosti moˇzemo staviti
a
= 0 i
b
= 1. Neka je
N
do-
voljno velik prirodan broj te neka je
t
j
=
j
N
, 0
≤
j
≤
N
. Ukoliko je
f
neprekinuta, moˇzemo njezine
vrijednosti na intervalu [
t
j
−
1
, t
j
i
aproksimirati s
f
(
t
j
). Stoga, funkciju
f
moˇzemo aproksimirati
vektorom
f
N
= (
f
(
t
1
)
, f
(
t
2
)
, . . . , f
(
t
N
))
∈
R
N
.
Oˇcito, ˇsto je broj
N
ve´ci, dobivamo bolju aproksimaciju funkcije
f
.
Ako su
f
i
g
dva signala u
L
2
([0
,
1]), onda ih moˇzemo diskretizirati na opisani naˇcin, kao
vektore
f
N
i
g
N
. Kako bismo definirali skalarni produkt
h
f, g
i
L
2
promotrimo standardni skalarni
produkt vektora
f
N
i
g
N
na prostoru
R
N
, kada broj
N
raste:
h
f
N
, g
N
i
R
N
=
N
X
j
=1
f
(
t
j
)
g
(
t
j
) =
N
X
j
=1
f
µ
j
n
¶
g
µ
j
n
¶
.
Problem u opisanom pristupu je u tome da kada
N
teˇzi u beskonaˇcnost, tada i suma na desnoj
strani prethodne jednakosti u pravilu teˇzi k beskonaˇcnosti. Stoga je bolji izbor srednja vrijednost
prethodnog skalarnog produkta, odnosno
1
N
h
f
N
, g
N
i
R
N
=
N
X
j
=1
f
µ
j
n
¶
g
µ
j
n
¶
1
N
.
Kako se vektori
f
N
i
g
N
pribliˇzavaju funkcijama
f
i
g
kada
N
raste, razumljivo je da za definiciju
skalarnog produkta
h
f, g
i
L
2
uzmemo graniˇcnu vrijednost prethodne srednje vrijednosti skalarnog
produkta, kada
N
teˇzi u beskonaˇcnost.
Prethodnu relaciju moˇzemo zapisati u obliku
1
N
h
f
N
, g
N
i
R
N
=
N
X
j
=1
f
(
t
j
)
g
(
t
j
)∆
t,
gdje je ∆
t
=
1
N
.
Ta suma predstavlja integralnu sumu za integral
R
1
0
f
(
t
)
g
(
t
)
dt
s obzirom na razdiobu [0
, t
1
, t
2
, . . . , t
N
]
segmenta [0
,
1]. Dakle, razumno je skalarni produkt na
L
2
([0
,
1]) definirati kao
h
f, g
i
=
R
1
0
f
(
t
)
g
(
t
)
dt
.
Opisana motivacija nam daje sljede´cu definiciju:
Definicija 1.5.
Skalarni produkt na
L
2
([
a, b
])
definiran je relacijom
h
f, g
i
L
2
=
Z
b
a
f
(
t
)
g
(
t
)
dt,
f, g
∈
L
2
([
a, b
])
.
Taj skalarni produkt ˇcesto nazivamo i
L
2
skalarnim produktom. Lagano se provjerava da tako
definirani skalarni produkt doista zadovoljava svojstva konjugirane simetriˇcnosti, homogenosti i
aditivnosti, iz definicije skalarnog produkta.
Promotrimo svojstvo pozitivnosti skalarnog produkta. Ako je funkcija
f
neprekinuta onda se
lagano pokazuje da relacija 0 =
h
f, f
i
=
R
b
a
|
f
(
t
)
|
2
dt
povlaˇci da je
f
(
t
) = 0,
∀
t
∈
[
a, b
]. Ako funkcija
7
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































