Tradicionalni brojni sistem, koji se izu
č
ava u školi, i koji se koristi u
svakodnevnom
ž
ivotu, naziva se dekadni brojni sistem.
U ovakvom sistemu, broj se predstavlja nizom cifara, a poziciji
svake cifre odgovara odre
đ
ena te
ž
ina (zna
č
aj).
1863=11000+8100+610+31.
Uopšteno, broj S oblika c
2
c
1
c
0
.c
-1
c
-2
ima vrijednost
S=c
2
10
2
+c
1
10
1
+c
0
10
0
+c
-1
10
-1
+c
-2
10
-2
.
Ovdje se 10 naziva osnova brojnog sistema (dekadni brojni
sistem) i jednaka je broju cifara koje se koriste u ovom sistemu
0,1,2,3,4,5,6,7,8,9.
U opštem slu
č
aju, vrijednost proizvoljnog broja S u brojnom
sistemu sa osnovom B jednaka je
:
S
c B
i
i
i
n
p
=
=−
−
∑
1
gdje je
0
1
≤
≤ −
c
B
i
Proceduru pretvaranja brojeva iz dekadnog u binarni brojni sistem
ilustrova
ć
emo na primjeru broja 637.14.
318:2=159
159:2=79
79:2=39
39:2=19
19:2=9
9:2=4
4:2=2
2:2=1
1:2=0
637:2=318
1
0
1
1
1
1
1
0
0
1
ostatak
zapis
0.14x2=0.28
0.28x2=0.56
0.56x2=1.12
0.12x2=0.24
0.24x2=0.48
0.48x2=0.96
0.96x2=1.92
0.92x2=1.84
0.84x2=1.68
0.68x2=1.36
0
0
1
0
0
0
1
1
1
1
zapis
O
č
igledno, je da va
ž
i jednakost 637.1410=1001111101.0010001111...2, iz koje
se zapa
ž
a da je dobijen binarni broj sa deset mjesta iza zareza, a da, ni sa tih
deset mjesta, nije potpuno ta
č
no odre
đ
en.
Oktalni brojni sistem
Oktalni brojni sistem ima za osnovu B=8, a brojevi u njemu
zapisuju se pomo
ć
u cifara iz skupa od osam elemenata
{0,1,2,3,4,5,6,7}.
B
roj 1175.107534 iz ovog sistema, saglasno izrazu (13.1), ima
sumu
:
1 8
1 8
7 8
5 8
1 8
0 8
7 8
5 8
3 8
4 8
637 14
3
2
1
0
1
2
3
4
5
6
×
+ ×
+ ×
+ ×
+
+ ×
+ ×
+ ×
+ ×
+ ×
+ ×
=
=
−
−
−
−
−
−
.
Pri konverziji iz binarnog u oktalni brojni sistem, binarni broj se dijeli u grupe sa po tri
cifre, pa se te grupe pretvore u dekadni sistem i tako dobijene cifre po redosljedu
grupisanja zapišu.
PRIMJER
Pretvoriti binarni broj 1011010111.10 u oktalni broj.
1
1 1
1
1 1 1
1
1
0
0
0
0 0
0
0
.
3
2
7 .
4
po tri cifre
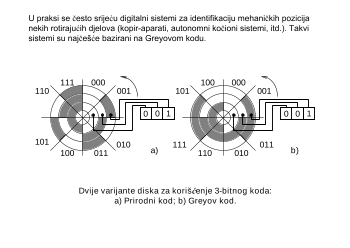
Heksadecimalni brojni sistem
Heksadecimalni brojni sistem ima za osnovu B=16, a brojevi u
ovom
sistemu
imaju
cifre
iz
skupa
{0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, gdje: A, B, C, D, E i F
odgovaraju u dekadnom sistemu vrijednostima: 10, 11, 12, 13, 14
i 15, respektivno.
Pretvaranje brojeva iz binarnog u heksadecimalni brojni sistem je sli
č
no
pretvaranju brojeva iz binarnog u oktalni brojni sistem, s tim što se ovdje
grupisanje vrši u po
č
etiri cifre.
PRIMJER
Pretvoriti binarni broj 1011011110.1 u heksadecimalni broj
1
1 1
1
1 1
1
0
0
0
0 0
0
0
.
.
1
2
D
E
8
po ~etiri cifre
0
