
Ispitivanje funkcija
XIII
i
XIV
dvoqas vebi — Vladimir Balti
14. Ispitivanje funkcija
Ovde je dat kratak pregled
XIII
i
XIV
dvoqasa vebi. Potrebno je da obnovite odgovarajuu teorijsku
materiju koja je obraena na predavanjima i u ubeniku.
Kako se najveim delom na vebama rade zadaci iz zbirke, nakon broja zadatka plavom bojom je oznaqen
broj zadatka u zbirci ”MATEMATIKA 1” profesora R. Lazovia, D. oria i . Jovanova u formi
p.z
, gde je
p
broj poglavlja, a
z
broj zadatka u tom poglavlju. Ovi zadaci sa preostalima iz zbirke
(iz poglavlja ”14. Ispitivanje funkcija”, kao i onim iz poglavlja ”15. Drugi kolokvijum” koji su vezani
za ovu materiju) qine celinu dovoljnu za pripremu ove oblasti.
Teorijski uvod
Ispitivanje funkcija je centralni i svakako najbitniji deo svakog kursa matematike. On daje matematiqku
osnovu za skiciranje grafika na osnovu matematiqke formule odreenih pojava koje se javljaju u ekonomiji,
prirodnim naukama, tehnici, fizici...
To je i uvek 4. zadatak na pismenom delu ispita!
Da ne bi imali problema sa ispitivanjem toka funkcije potrebno je da dobro svladate rexavanje jednaqi-
na i nejednaqina (to je srednjoxkolska matematika), odreivanje graniqnih vrednosti (limesa) i raqunanje
izvoda funkcije.
Mi emo ispitivanje funkcija razloiti na sedam delova:
1. Oblast definisanosti funkcije (ili domen funkcije)
2. Nule, znak funkcije i presek sa
y
-osom
3. Parnost i periodiqnost funkcije
4. Graniqne vrednosti funkcije na krajevima domena i asimptote funkcije
5. Prvi izvod, monotonost i lokalni ekstremi funkcije
6. Drugi izvod, konveksnost i prevojne taqke funkcije
7. Crtanje grafika funkcije.
Sada emo se detaljnije osvrnuti na svaki od ovih delova.
Na osnovu svih prethodno odreenih taqaka crtamo grafik funkcije. Ukoliko se neke 2 taqke ne slau
meusobno ne nastavljamo sa radom, nego se osvrnemo i ako moemo utvrdimo gde je grexka (jer bi nastavak
rada mogao da prouzrokuje jox grexaka).
Na grafiku oznaqavamo (ako postoje) sledee taqke: nule, presek sa
y
-osom – to je taqka
(0
, f
(0))
, minimume
i maksimume, prevojne taqke, zatim crtamo asimptote i oznaqavamo (crticama) graniqne vrednosti i na kraju
sve to spojimo vodei raquna o znaku, monotonosti i konveksnosti. Ako se nexto ne slae, to je pokazatelj
da smo naqinili neku grexku u raqunu neke od prethodnih stavki! Takoe na pozitivnom smeru
x
-ose treba
staviti strelicu i
x
, a na pozitivnom smeru
y
-ose treba staviti strelicu i
f
(
x
)
.
Naredni grafici vam daju predstavu kako izgleda funkcija (oni su dobijeni korixenjem programskog
paketa Mejpl), ali na njima morate da oznaqite sve gore navedeno. Takoe od vas se ne oqekuju prirodne
proporcije nego samo da skicirate grafik (znaqi, da vodite raquna o znaku, monotonosti i konveksnosti, kao
i kakav je meusobni odnos odgovarajuih taqaka i pravih – xta je pre, xta je gore...). Pribline vrednosti
koordinata slue za te procene, ali se od vas ne oqekuje da to radite na ispitu!
Zadaci
Ispitati tok i skicirati grafik sledeih funkcija:
1.
14.42.
f
(
x
) =
x
3
−
3
x
x
2
−
1
.
Rexenje.
1
◦
Funkcija
f
(
x
)
je definisana kada su definisane funkcije
g
(
x
) =
x
3
−
3
x
i
h
(
x
) =
x
2
−
1
(xto je
uvek jer su polinomi definisani za svako
x
∈
R
) i kada je
h
(
x
) =
x
2
−
1
6
= 0
, tj.
x
2
6
= 1
, odnosno
x
6
=
±
1
.
Stoga je domen funkcije
f
jednak
D
= (
−∞
,
−
1)
∪
(
−
1
,
1)
∪
(1
,
+
∞
)
.
2
◦
f
(0) =
0
3
−
3
·
0
0
2
−
1
= 0
, pa je presek sa
y
-osom taqka
Y
(0
,
0)
.
1
Datu funkciju moemo predstaviti u obliku
f
(
x
) =
x
(
x
2
−
3)
x
2
−
1
.
Odavde odreujemo nule i znak na osnovu tablice u kojoj imamo znak svakog qlana ponaosob:
(
−∞
,
−
√
3)
−
√
3
(
−
√
3
,
−
1)
−
1
(
−
1
,
0)
0
(0
,
1)
1
(1
,
√
3)
√
3
(
√
3
,
+
∞
)
x
−
−
−
−
−
0
+
+
+
+
+
x
2
−
3
+
0
−
−
−
−
−
−
−
0
+
x
2
−
1
+
+
+
x
−
−
−
x
+
+
+
f
(
x
)
−
0
+
x
−
0
+
x
−
0
+
Dobijamo da je funkcija
f
(
x
)
ima nule
x
=
−
√
3
,
x
= 0
i
x
=
√
3
, kao i da je
f
(
x
)
<
0
za
x
∈
(
−∞
,
−
√
3)
∪
(
−
1
,
0)
∪
(1
,
√
3)
, a
f
(
x
)
>
0
za
x
∈
(
−
√
3
,
−
1)
∪
(0
,
1)
∪
(
√
3
,
+
∞
)
.
3
◦
Kako je
f
(
−
x
) =
−
x
¡
(
−
x
)
2
−
3
¢
(
−
x
)
2
−
1
=
−
x
(
x
2
−
3)
x
2
−
1
=
−
f
(
x
)
za
∀
x
∈
D
dobijamo da je funkcija
f
(
x
)
neparna.
Grafik ove funkcije je centralno simetriqan u odnosu na koordinatni poqetak
O
(0
,
0)
.
Funkcija
f
(
x
)
nije ni periodiqna.
Dokaz: pretpostavimo suprotno, tj. da je periodiqna sa periodom
T
. Tada je
f
(
x
+
T
) =
f
(
x
)
za
∀
x
∈
D
, ali
ako bi uzeli
x
=
−
1
−
T
dobijamo kontradikciju
f
(
−
1) =
f
(
−
1
−
T
)
– to je nemogue jer za
−
1
funkcija nije
definisana, a za
−
1
−
T
jeste).
4
◦
Kako je domen
D
= (
−∞
,
−
1)
∪
(
−
1
,
1)
∪
(1
,
+
∞
)
potrebno je odrediti sledeih xest limesa:
lim
x
→−∞
f
(
x
)
,
lim
x
→−
1
−
f
(
x
)
,
lim
x
→−
1
+
f
(
x
)
,
lim
x
→
1
−
f
(
x
)
,
lim
x
→
1
+
f
(
x
)
,
lim
x
→
+
∞
f
(
x
)
.
lim
x
→−∞
f
(
x
) = lim
x
→−∞
x
3
−
3
x
x
2
−
1
= lim
x
→−∞
x
3
−
3
x
x
2
−
1
·
1
x
2
1
x
2
= lim
x
→−∞
x
−
3
x
1
−
1
x
2
=
−∞
jer kad
x
→ −∞
onda
3
x
→
0
i
1
x
2
→
0
.
lim
x
→−
1
−
f
(
x
) = lim
x
→−
1
−
x
3
−
3
x
x
2
−
1
=
·
(
−
1)
3
−
3
·
(
−
1)
(
−
1
−
)
2
−
1
=
4
1
+
−
1
=
4
0
+
¸
= +
∞
.
Potpuno analogno se dobijaju
lim
x
→−
1
+
f
(
x
) =
−∞
,
lim
x
→
1
−
f
(
x
) = +
∞
i
lim
x
→
1
+
f
(
x
) =
−∞
.
lim
x
→
+
∞
f
(
x
)
moemo izraqunati kao i
lim
x
→−∞
f
(
x
)
, ali emo ovde uraditi na drugi naqin, pomou Lopitalovog
pravila jer je to limes oblika
∞
∞
:
lim
x
→
+
∞
f
(
x
) = lim
x
→
+
∞
x
3
−
3
x
x
2
−
1
L.P.
=
∞
∞
lim
x
→
+
∞
3
x
2
−
3
2
x
L.P.
=
∞
∞
lim
x
→
+
∞
6
x
2
= +
∞
.
Asimptote:
Kako smo dobili da je
lim
x
→−
1
−
f
(
x
) = +
∞
(a i
lim
x
→−
1
+
f
(
x
) =
−∞
) prava
x
=
−
1
je vertikalna
asimptota.
Kako je
lim
x
→
1
−
f
(
x
) = +
∞
(a i
lim
x
→
1
+
f
(
x
) =
−∞
) i prava
x
= 1
je vertikalna asimptota.
Kako su
lim
x
→−∞
f
(
x
)
i
lim
x
→
+
∞
f
(
x
)
beskonaqni funkcija nema horizontalnih asimptota, ali moe imati kosih.
Kako se svi limesi potpuno analogno raqunaju i za
x
→ −∞
i za
x
→
+
∞
, svuda emo pisati
x
→ ±∞
.
k
= lim
x
→±∞
f
(
x
)
x
= lim
x
→±∞
x
3
−
3
x
x
2
−
1
x
= lim
x
→±∞
x
3
−
3
x
x
3
−
x
= lim
x
→±∞
x
3
−
3
x
x
3
−
x
·
1
x
3
1
x
3
= lim
x
→±∞
1
−
3
x
2
1
−
1
x
2
= 1
.
Ovaj limes je konaqan i
6
= 0
, pa traimo koeficijent
n
:
n
= lim
x
→±∞
f
(
x
)
−
k
·
x
= lim
x
→±∞
x
3
−
3
x
x
2
−
1
−
1
·
x
= lim
x
→±∞
x
3
−
3
x
−
x
3
+
x
x
2
−
1
= lim
x
→±∞
−
2
x
x
2
−
1
L.P.
=
∞
∞
lim
x
→±∞
−
2
2
x
=
·
−
2
∞
¸
= 0
.
I ovaj limes je konaqan. Stoga je prava
y
= 1
·
x
+ 0
, tj.
y
=
x
obostrana kosa asimptota.
5
◦
f
0
(
x
) =
x
4
+ 3
(
x
−
1)
2
(
x
+ 1)
2
. Svi qlanovi u ovom izrazu su pozitivni pa dobijamo:
(
−∞
,
−
1)
−
1
(
−
1
,
1)
1
(1
,
+
∞
)
x
4
+ 3
+
+
+
+
+
(
x
−
1)
2
+
+
+
x
+
(
x
+ 1)
2
+
x
+
+
+
f
0
(
x
)
+
x
+
x
+
f
(
x
)
%
x
%
x
%
Funkcija je rastua na intervalima:
(
−∞
,
−
1)
,
(
−
1
,
1)
i
(1
,
+
∞
)
. Nema ekstremnih taqaka.
2
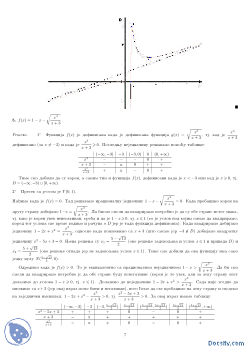
Grafik ove funkcije je centralno simetriqan u odnosu na koordinatni poqetak
O
(0
,
0)
.
Funkcija
f
(
x
)
nije ni periodiqna.
Dokaz: pretpostavimo suprotno, tj. da je periodiqna sa periodom
T
, tj.
f
(
x
+
T
) =
f
(
x
)
za
∀
x
∈
D
. Tada se i
nule periodiqno ponavljaju , pa ako bi uzeli
x
=
−
T
dobijamo kontradikciju
f
(0) =
f
(
−
T
)
– xto je nemogue
jer
f
(0) = 0
, a
f
(
−
T
)
<
0
).
4
◦
Kako je domen
D
= (
−∞
,
+
∞
)
potrebno je odrediti dva limesa:
lim
x
→−∞
f
(
x
)
i
lim
x
→
+
∞
f
(
x
)
. Njih istovremeno
traimo:
lim
x
→±∞
f
(
x
) = lim
x
→±∞
arcsin
2
x
1 +
x
2
= lim
x
→±∞
arcsin
µ
2
x
1 +
x
2
·
1
x
2
1
x
2
¶
= lim
x
→±∞
arcsin
1
x
1
x
2
+ 1
= arcsin 0 = 0
.
Kako domen nema prekida (tj.
f
(
x
)
je definisana na celom skupu
R
) to
f
(
x
)
nema vertikalnih asimptota.
Kako je
lim
x
→±∞
f
(
x
) = lim
x
→±∞
arcsin
2
x
1 +
x
2
= 0
) prava
y
= 0
je obostrana horizontalna asimptota.
Kako funkcija ima horizontalnu asimptotu (sa obe strane) to ona nema kosih asimptota.
5
◦
f
0
(
x
) =
2
−
2
x
2
(
x
2
+ 1)
2
s
(
x
2
−
1)
2
(
x
2
+ 1)
2
=
2(1
−
x
2
)
(
x
2
+ 1)
2
·
|
x
2
−
1
|
x
2
+ 1
, pa dobijamo da je
f
0
(
x
) =
−
2
1+
x
2
,
x <
−
1
2
1+
x
2
,
−
1
< x <
1
−
2
1+
x
2
,
x >
1
.
Odavde dobijamo znak prvog izvoda:
(
−∞
,
−
1)
−
1
(
−
1
,
1)
1
(1
,
+
∞
)
f
0
(
x
)
−
x
+
x
−
f
(
x
)
&
min
%
max
&
Funkcija je rastua na
(
−
1
,
1)
, a opadajua na
(
−∞
,
−
1)
, i na
(1
,
+
∞
)
.
Minimum je taqka
M
1
(
−
1
,
−
π
2
)
, a maksimum je
M
2
(1
,
π
2
)
.
Napomena.
Naglasimo da u taqkama
M
1
i
M
2
funkcija
f
(
x
)
ima xpic (u tim taqkama funkcija jeste neprekidna,
ali nije diferencijabilna). Koeficijent pravca tangente na krivu sa leve strane taqke
M
1
je
k
1
=
f
0
−
(
−
1) =
−
1
, a sa desne strane je
k
2
=
f
0
+
(
−
1) = 1
(stoga se ove 2 krive u taqki
M
1
seku pod uglom od
90
◦
— prva sa
x
-osom
zaklapa ugao od
45
◦
jer je
k
1
= tg
ϕ
1
=
−
1
⇒
ϕ
1
=
−
45
◦
i sliqno za drugu imamo da je
k
2
= tg
ϕ
2
= 1
⇒
ϕ
2
= 45
◦
).
(Ova analiza xpiceva se ne oqekuje od studenata na ispitu!)
6
◦
f
00
(
x
) =
4
x
(1+
x
2
)
2
,
x <
−
1
−
4
x
(1+
x
2
)
2
,
−
1
< x <
1
4
x
(1+
x
2
)
2
,
x >
1
i odavde imamo tablicu:
(
−∞
,
−
1)
−
1
(
−
1
,
0)
0
(0
,
1)
1
(1
,
+
∞
)
f
00
(
x
)
−
x
+
0
−
x
+
f
(
x
)
∩
P
1
∪
P
2
∩
P
3
∪
Funkcija ima prevojne taqke:
P
1
=
M
1
(
−
1
,
−
π
2
)
,
P
2
=
Y
(0
,
0)
i
P
3
=
M
2
(1
,
π
2
)
.
4
3.
f
(
x
) = ln
µ
1
−
1
x
¶
2
.
Rexenje.
1
◦
Funkcija
f
(
x
)
je definisana kada je definisana funkcija
g
(
x
) =
µ
1
−
1
x
¶
2
(xto je za
x
6
= 0
) i
kada je
g
(
x
)
>
0
, a kako je
g
(
x
)
taqan kvadrat to je ekvivalentno sa
1
−
1
x
6
= 0
odakle dobijamo i
x
6
= 1
.
Time smo dobili da je data funkcija definisana kada je
x
6
= 0
i
x
6
= 1
, tj.
D
= (
−∞
,
0)
∪
(0
,
1)
∪
(1
,
+
∞
)
.
2
◦
Presek sa
y
-osom nemamo jer
0
6∈
D
.
f
(
x
)
>
0
kad je
ln
µ
1
−
1
x
¶
2
>
0 = ln 1
, odnosno kad je
µ
1
−
1
x
¶
2
>
1
, tj.
1
−
2
x
x
2
>
0
, pa dobijamo da funkcija
f
(
x
)
ima nulu
x
=
1
2
, kao i da je
f
(
x
)
>
0
za
x
∈
(
−∞
,
0)
∪
(0
,
1
2
)
, a
f
(
x
)
<
0
za
x
∈
(
1
2
,
1)
∪
(1
,
+
∞
)
.
3
◦
Funkcija
f
(
x
)
nije ni parna ni neparna ni periodiqna (to zakljuqujemo na osnovu
D
).
4
◦
Kako je domen
D
= (
−∞
,
0)
∪
(0
,
1)
∪
(1
,
+
∞
)
potrebno je odrediti sledeih xest limesa:
lim
x
→−∞
f
(
x
)
,
lim
x
→
0
−
f
(
x
)
,
lim
x
→
0
+
f
(
x
)
,
lim
x
→
1
−
f
(
x
)
,
lim
x
→
1
+
f
(
x
)
,
lim
x
→
+
∞
f
(
x
)
.
lim
x
→±∞
f
(
x
) = lim
x
→±∞
ln
µ
1
−
1
x
¶
2
= ln 1 = 0
.
lim
x
→
0
−
f
(
x
) = lim
x
→
0
−
ln
µ
1
−
1
x
¶
2
=
"
ln
µ
1
−
1
0
−
¶
2
= ln(+
∞
)
2
= ln(+
∞
)
#
= +
∞
.
Potpuno analogno se dobija i
lim
x
→
0
+
f
(
x
) = +
∞
.
lim
x
→
1
−
f
(
x
) = lim
x
→
1
−
ln
µ
1
−
1
x
¶
2
=
"
ln
µ
1
−
1
1
−
¶
2
= ln
¡
1
−
1
+
¢
2
= ln(0
−
)
2
= ln(0
+
)
#
=
−∞
.
Potpuno analogno se dobija i
lim
x
→
1
+
f
(
x
) =
−∞
.
Kako je
lim
x
→
0
−
f
(
x
) = +
∞
(a i
lim
x
→
0
+
f
(
x
) = +
∞
) prava
x
= 0
je vertikalna asimptota (i to sa obe strane).
Kako je
lim
x
→
1
−
f
(
x
) =
−∞
(a i
lim
x
→
1
+
f
(
x
) =
−∞
) i prava
x
= 1
je vertikalna asimptota (sa obe strane).
Kako je
lim
x
→±∞
f
(
x
) = 0
prava
y
= 0
je obostrana horizontalna asimptota.
Kako funkcija ima horizontalnu asimptotu (sa obe strane) to ona nema kosih asimptota.
5
◦
f
0
(
x
) =
2
x
(
x
−
1)
, pa imamo tabelu:
(
−∞
,
0)
0
(0
,
1)
1
(1
,
+
∞
)
x
−
x
+
+
+
x
−
1
−
−
−
x
+
f
0
(
x
)
+
x
−
x
+
f
(
x
)
%
x
&
x
%
Funkcija je rastua na
(
−∞
,
0)
i na
(1
,
+
∞
)
, a opadajua na
(0
,
1)
. Lokalnih ekstrema nema.
6
◦
f
00
(
x
) =
2
−
4
x
x
2
(
x
−
1)
2
i odavde imamo tablicu:
(
−∞
,
0)
0
(0
,
1
2
)
1
2
(
1
2
,
1)
1
(1
,
+
∞
)
2
−
4
x
+
+
+
0
−
−
−
x
2
+
x
+
+
+
+
+
(
x
−
1)
2
+
+
+
+
+
x
+
f
00
(
x
)
+
x
+
0
−
x
−
f
(
x
)
∪
x
∪
P
∩
x
∩
Funkcija ima prevojnu taqku:
P
(0
,
0)
.
5
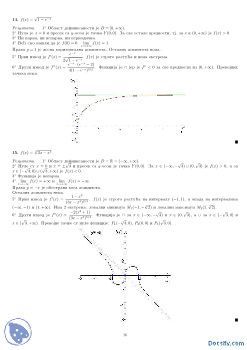
5.
f
(
x
) = 1
−
x
−
r
x
3
x
+ 3
.
Rexenje.
1
◦
Funkcija
f
(
x
)
je definisana kada je definisana funkcija
g
(
x
) =
r
x
3
x
+ 3
, tj. kad je
x
3
x
+ 3
definisano (za
x
6
=
−
3
) i kada je
x
3
x
+ 3
⩾
0
. Poslednju nejednaqinu rexavamo pomou tablice:
(
−∞
,
−
3)
−
3
(
−
3
,
0)
0
(0
,
+
∞
)
x
3
−
−
−
0
+
x
+ 3
−
x
0
+
+
x
3
x
+3
+
x
−
0
+
Time smo dobili da su koren, a samim tim i funkcija
f
(
x
)
, definisani kada je
x <
−
3
ili kad je
x
⩾
0
, tj.
D
= (
−∞
,
−
3)
∪
[0
,
+
∞
)
.
2
◦
Presek sa
y
-osom je
Y
(0
,
1)
.
Naimo kada je
f
(
x
) = 0
. Tad rexavamo iracionalnu jednaqinu
1
−
x
−
r
x
3
x
+ 3
= 0
. Kada prebacimo koren na
drugu stranu dobijamo
1
−
x
=
r
x
3
x
+ 3
. Da bismo smeli da kvadriramo potrebno je da su obe strane istog znaka,
tj. kako je koren uvek nenegativan, treba i da je
1
−
x
⩾
0
, tj.
x
⩽
1
(to je uslov pod kojim smemo da kvadriramo;
pored tog uslova sve vreme vodimo i raquna o
D
jer je tada funkcija definisana). Kada kvadriramo dobijamo
jednaqinu
1
−
2
x
+
x
2
=
x
3
x
+ 3
, odnosno kada pomnoimo sa
x
+ 3
(xto smemo jer
−
3
6∈
D
) dobijamo kvadratnu
jednaqinu
x
2
−
5
x
+ 3 = 0
. Njena rexenja su
x
1
=
5
−
√
13
2
(ovo rexenje zadovoljava i uslov
x
⩽
1
i pripada
D
) i
x
2
=
5 +
√
13
2
(ovo rexenje otpada jer ne zadovoljava uslov
x
⩽
1
). Time smo dobili da ova funkciju ima samo
jednu nulu
N
(
5
−
√
13
2
,
0)
.
Odredimo kada je
f
(
x
)
>
0
. To je ekvivalentno sa iracionalnom nejednaqinom
1
−
x >
r
x
3
x
+ 3
. Da bi smo
smeli da kvadriramo potrebno je da obe strane budu nenegativne (koren je to uvek, ali za levu stranu opet
dolazimo do uslova
1
−
x
⩾
0
, tj.
x
⩽
1
). Dolazimo do nejednaqine
1
−
2
x
+
x
2
>
x
3
x
+ 3
. Sada nije zgodno da
mnoimo sa
x
+ 3
(jer ovaj izraz moe biti i negativan), nego emo da sve prebacimo na levu stranu i svedemo
na zajedniqki imenilac:
1
−
2
x
+
x
2
−
x
3
x
+ 3
>
0
, tj.
x
2
−
5
x
+ 3
x
+ 3
>
0
. Za ovaj izraz imamo tablicu:
(
−∞
,
−
3)
−
3
(
−
3
,
5
−
√
13
2
)
5
−
√
13
2
(
5
−
√
13
2
,
5+
√
13
2
)
5+
√
13
2
(
5+
√
13
2
,
+
∞
)
x
2
−
5
x
+ 3
+
+
+
0
−
0
+
x
+ 3
−
x
+
+
+
+
+
x
3
x
+3
−
x
+
0
−
0
+
7
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































