
Linearno programiranje
Financijsko odlučivanje
Financijsko odlučivanje
Martina Briš
Martina Briš
Rješenje pomoću LINDO programa
Rješenje pomoću LINDO programa
Računala skoro uvijek rješavaju realne linearne programe pomoću simpleks
Računala skoro uvijek rješavaju realne linearne programe pomoću simpleks
metode. Koeficijenti u funkciji cilja poznati su pod nazivom koeficijenti
metode. Koeficijenti u funkciji cilja poznati su pod nazivom koeficijenti
troškova (jer se za vrijeme drugog svijetskog rata , prvi program iz LP bavio
troškova (jer se za vrijeme drugog svijetskog rata , prvi program iz LP bavio
problemom minimalizacije troškova). Uz funkciju cilja u modelu se nalaze
problemom minimalizacije troškova). Uz funkciju cilja u modelu se nalaze
tehnološki koeficijenti i vrijednosti desne strane.
tehnološki koeficijenti i vrijednosti desne strane.
Rasprostranjeni software za LP je LINDO paket. Ime LINDO je izvedenica iz
Rasprostranjeni software za LP je LINDO paket. Ime LINDO je izvedenica iz
L
L
inear
inear
IN
IN
teractive
teractive
D
D
iscrete
iscrete
O
O
ptimization
ptimization
. Riječ “discret” znači skakanje s
. Riječ “discret” znači skakanje s
jednog na drugo bazično rješenje umjesto da se kruži u okviru dopuštenog
jednog na drugo bazično rješenje umjesto da se kruži u okviru dopuštenog
područja u potrazi za optimalnim rješenjem (ako ono postoji).
područja u potrazi za optimalnim rješenjem (ako ono postoji).
LINDO koristiu simpleks metodu. Uz rješenje problema ovaj program daje
LINDO koristiu simpleks metodu. Uz rješenje problema ovaj program daje
običnu analizu osjetljivosti funkcije cilja (Objective Function Coefficients
običnu analizu osjetljivosti funkcije cilja (Objective Function Coefficients
(zvanu Cost Coefficients) i desne strane (Right- hand- side RHS) ograničenja.
(zvanu Cost Coefficients) i desne strane (Right- hand- side RHS) ograničenja.
Riješimo problem stolara pomoću LINDO paketa. U prozor (window)
Riješimo problem stolara pomoću LINDO paketa. U prozor (window)
utipkajmo:
utipkajmo:
MAX 5X1 + 3X2
MAX 5X1 + 3X2
S.T. 2X1 + X2 ≤ 40
S.T. 2X1 + X2 ≤ 40
X1 + 2X2 ≤ 50
X1 + 2X2 ≤ 50
End
End
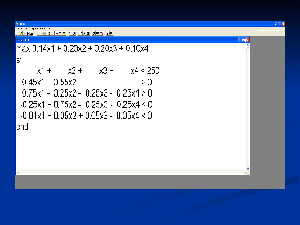
Primjer: Financijsko planiranje
Primjer: Financijsko planiranje
Banka daje četiri vrste kredita svojim klijentima zaračunavajući im slijedeće
Banka daje četiri vrste kredita svojim klijentima zaračunavajući im slijedeće
godišnje kamate:
godišnje kamate:
Prvi hipotekarni kredit 14%
Prvi hipotekarni kredit 14%
Drugi hipotekarni kredit 20%
Drugi hipotekarni kredit 20%
Kredit za domaćinstvo 20%
Kredit za domaćinstvo 20%
Osobna potrošnja 10%
Osobna potrošnja 10%
Banka ima na raspolaganju za kreditiranje maksimalno 250 milijuna novčanih
Banka ima na raspolaganju za kreditiranje maksimalno 250 milijuna novčanih
jedinica (NJ). Daljnja ograničenja su:
jedinica (NJ). Daljnja ograničenja su:
Prvi hipotekarni kredit mora biti barem 55% od svih hipotekarnih kredita
Prvi hipotekarni kredit mora biti barem 55% od svih hipotekarnih kredita
koji se koriste i barem 25% od ukupne sume predviđene za kreditiranje.
koji se koriste i barem 25% od ukupne sume predviđene za kreditiranje.
Drugi hipotekarni kredit ne smije premašiti 25 % od svih kredita.
Drugi hipotekarni kredit ne smije premašiti 25 % od svih kredita.
Da bi se izbjeglo javno nezadovoljstvo i uvođenje novih taksa, prosječna
Da bi se izbjeglo javno nezadovoljstvo i uvođenje novih taksa, prosječna
stopa kamata na sve kredite ne smije premašiti 15 %.
stopa kamata na sve kredite ne smije premašiti 15 %.
Formulirajmo problem alokacije kredita kao problem linearnog programiranja u
Formulirajmo problem alokacije kredita kao problem linearnog programiranja u
kojemu banka maksimizira svoj interes kroz kamate uz zadovoljavanje
kojemu banka maksimizira svoj interes kroz kamate uz zadovoljavanje
postavljenih ograničenja. Uočimo da ograničenja koja se odnose na kreditnu
postavljenih ograničenja. Uočimo da ograničenja koja se odnose na kreditnu
politiku banke ograničavaju s jedne strane profit, ali isto tako i smanjuju njeno
politiku banke ograničavaju s jedne strane profit, ali isto tako i smanjuju njeno
izlaganje riziku alocirajući novac na različita područja.
izlaganje riziku alocirajući novac na različita područja.
Rješenje
Rješenje
Odredimo:
Odredimo:
Varijable
Varijable
Ograničenja
Ograničenja
Cilj
Cilj
Verbalnu deskripciju pretvaramo u ekvivalentnu matematički formulaciju. Prije
Verbalnu deskripciju pretvaramo u ekvivalentnu matematički formulaciju. Prije
nego se postavi matematička formulacija linearnog programiranja (LP) korisno
nego se postavi matematička formulacija linearnog programiranja (LP) korisno
je izraziti varijable, ograničenja i cilj.
je izraziti varijable, ograničenja i cilj.
Varijable
Varijable
U biti smo zainteresirani za svotu kojom banka kreditira klijente u svakoj od
U biti smo zainteresirani za svotu kojom banka kreditira klijente u svakoj od
četiri različitih kategorija (ne aktualne nositelje takvih kredita)
četiri različitih kategorija (ne aktualne nositelje takvih kredita)
Neka je
Neka je
xi = količina kredita u području i (gdje i =1 odgovara prvom hipotekarnom
xi = količina kredita u području i (gdje i =1 odgovara prvom hipotekarnom
kreditu, i =2 drugom, itd.) uzimajući u obzir xi
kreditu, i =2 drugom, itd.) uzimajući u obzir xi
0 (i=1,2,3,4).
0 (i=1,2,3,4).
Zapazimo da su u konvencionalnom LP-u sve varijable
Zapazimo da su u konvencionalnom LP-u sve varijable
0. Svaka varijabla
0. Svaka varijabla
(recimo x) koja može biti pozitivna ili negativna može se zapisati kao x1 - x2
(recimo x) koja može biti pozitivna ili negativna može se zapisati kao x1 - x2
(razlika između dvije nove varijable) gdje je
(razlika između dvije nove varijable) gdje je
x1
x1
0 i x2
0 i x2
0.
0.

Funkcija cilja
Funkcija cilja
Treba maksimizirati prihod od kamata
Treba maksimizirati prihod od kamata
max 0.14x1 +0.20x2 +0.20x3 +0.10x4
max 0.14x1 +0.20x2 +0.20x3 +0.10x4
U ovom slučaju optimalno rješenje linearnog programiranja ( rješenje
U ovom slučaju optimalno rješenje linearnog programiranja ( rješenje
pomoću softwearskog paketa) je
pomoću softwearskog paketa) je
x1 =208.33, x2 = 41.67 i x3 = x4 = 0.
x1 =208.33, x2 = 41.67 i x3 = x4 = 0.
Ovaj materijal je namenjen za učenje i pripremu, ne za predaju.
Slični dokumenti



























































