Mehanika fluida

111

6. Strujanje fluida 

Jedno je od najbitnijih svojstava fluida lako

ć

a kojom se fluid giba odnosno struji; i najmanje smi

č

no 

naprezanje, ili neravnoteža normalnog naprezanja (tlakova), uzrokovat 

ć

e kretanje fluida. Ne želimo li 

da se to doga

đ

a moramo posebnim mjerama ograni

č

avati gibanje fluida. 

Strujanje se fluida me

đ

utim, odnosno gibanje fluida, razlikuje od gibanja materijalne to

č

ke odnosno 

č

vrstog tijela. Kad se giba naime 

č

vrsto tijelo ne postoji relativno gibanje jedne 

č

estice (elementa) tijela 

u odnosu na druge. S druge strane pak, uslijed lake me

đ

usobne pomi

č

nosti 

č

estica (elemenata) fluida, 

brzine 

č

estica fluida, na raznim mjestima u fluidu što struji, u najop

ć

enitijem slu

č

aju, imaju razli

č

itu 

veli

č

inu i smjer. Duž nekog pravca primjerice, koji u nekom trenutku zamišljamo unutar struje

ć

eg fluida, 

imaju 

č

estice fluida op

ć

enito razne brzine u raznim pravcima tako da 

ć

e promatrani pravac, shvatimo li 

ga sastavljenim od 

č

estica fluida, u idu

ć

em trenutku poprimiti oblik neke zakrivljene crte koja 

ć

e se 

stalno, tijekom strujanja, mijenjati. Posljedi

č

no, analiza 

ć

e se strujanja fluida unekoliko razlikovati od 

analize gibanja materijalnih to

č

aka odnosno 

č

vrstih tijela. Njihovo gibanje naime, budu

ć

i da poznajemo 

mase tijela i razlikujemo ih me

đ

usobno, te da je njihov broj (prakti

č

no) ograni

č

en i poznat, možemo 

opisati na odvojeni i diskretni na

č

in. (To je tzv. Lagrangeov ili materijalni (supstancijalni) pristup.) 

Postavljamo pitanje : 

„koji je položaj tijela u prostoru u ovisnosti o vremenu, 

 

?"

r t





, 

i iz te obavijesti odre

đ

ujemo onda brzinu, akceleraciju i (rezultantnu) silu što djeluje na tijelo (tijela):  





2

( )

( )

,

;

.

dr t

d r t

c

a

sila

F

ma

m

konst

dt

dt























.  

Sli

č

ni (isti) postupak neprovediv je (nerealisti

č

an) s fluidom (s iznimkom specijalnih slu

č

ajeva) budu

ć

i 

da iole upotrebljivije koli

č

ine fluida sadrže preveliki (prakti

č

ki beskona

č

an) broj molekula. Zbog toga se, 

kao i da bismo omogu

ć

ili primjenu diferencijalnog (i integralnog) ra

č

una u analizama fluida, služimo 

hipotezom kontinuuma 

(o pojmu kontinuuma bilo je govora i u prvom dijelu udžbenika)

 smatraju

ć

i da se fluid 

sastoji od 

č

estica fluida koje djeluju me

đ

usobno i sa svojom okolicom. (Svaka 

č

estica fluida sadrži 

golem broj molekula.) Na taj na

č

in možemo opisati strujanje fluida opisuju

ć

i gibanje 

č

estica fluida, a ne 

njegovih molekula, odre

đ

uju

ć

i brzine i akceleracije 

č

estica fluida.  

Analiza se strujanja fluida pritom (odre

đ

ivanje njegovih fizikalnih svojstava) svodi stoga na jedan ili 

kombinacije ovih postupaka: 

A.

definiranje „individualnog, supstancijalnog ili materijalnog volumena“, što zna

č

i da 

ć

emo iz fluida 

izdvojiti odre

đ

enu i poznatu koli

č

inu, tj. poznatu i konstantnu masu fluida, dakle zatvoreni sustav, 

koji 

ć

emo zatim promatrati i analizirati tijekom njegovog gibanja; 

B.

prate

ć

i svaku od golemog broja 

č

estica fluida na putu kroz prostor ustanovljuju

ć

i kako se fizikalne 

osobine 

č

estica fluida mijenjaju u funkciji vremena; takav se na

č

in promatranja (opisivanja gibanja), 

prema re

č

enome, naziva Lagrangeovim (na

č

in promatranja koji se ve

ć

inom (pretežito) primjenjuje 

kad se analizira kretanje materijalne to

č

ke i 

č

vrstog tijela), a njegova je primjena (teoretski) mogu

ć

a 

budu

ć

i da su 

č

estice fluida konstantne mase, i/ili 

C.

prate

ć

i što se doga

đ

a s 

č

esticama fluida u nekoj (nekima) fiksnoj (fiksnim) to

č

ki (to

č

kama) 

prostora, ili u dijelu prostora kroz koji struji fluid, tzv. kontrolnom volumenu 

(vidjeti prvi udžbenik)

, 

s obzirom na odabrani koordinatni sustav, u koju (koje, koji) one pristižu u neprekidnom, 
kontinuiranom nizu jedna iza druge, što je tzv. Eulerov ili lokalni (mjesni) na

č

in promatranja.  

Npr., neka je kontrolni volumen to

č

ka 

č

ije su koordinate x

1

, y

1

, z

1

. U tom slu

č

aju možemo izraziti brzine 

č

estica 

fluida koje prolaze kroz tu to

č

ku ovako 





1

1

1

,

, , .

c

c x y z t







 To su dakle brzine kontinuiranog niza 

č

estica 

fluida koje prolaze to

č

kom x

1

, y

1

, z

1

. 

 
Uzrok gibanja 

č

estica fluida može biti jedna ili više sila koje na njih djeluju: 

a)

masene (volumenske) sile poput sile teže, inercijskih sila (npr. centrifugalne sile) i sl.; 

112

b)

površinske sile poput sila tlaka, koje nastaju zbog razlike tlakova u raznim to

č

kama fluida, ili 

adhezijske sile; 

c)

sile viskoziteta kao posljedica unutrašnjeg trenja me

đ

u 

č

esticama fluida i 

d)

elasti

č

ne sile (uglavnom kod plinova) zbog kompresibilnosti (stla

č

ivosti) fluida. 

 
Pri strujanju fluida razlikujemo: 

1.

protjecanje  
– strujanje fluida izme

đ

u krutih stijenki (cijevi, kanala i sl.); radi se o transportu fluida protokom, 

odnosno o transportu energije fluidom; 

2.

optjecanje  
– pojave relativnog i apsolutnog strujanja fluida oko nekog 

č

vrstog tijela uronjenog u fluid; radi 

se dakle o transportu 

č

vrstih tijela kroz fluid (brodovi, podmornice, letjelice itd.), ili, strujanju 

fluida oko 

č

vrstog tijela i 

3.

kombinaciju protjecanja i optjecanja  
– pojavljuje se npr. kod strujanja fluida izme

đ

u lopatica turbostrojeva jer se strujanje tada može 

promatrati kao protjecanje me

đ

u lopaticama ili kao optjecanje oko lopatica uronjenih u fluid. 

6.1 Vrste strujanja 

Ako su u svakoj 

č

vrstoj (fiksnoj) to

č

ki prostora, kojom struji fluid, sve fizikalne veli

č

ine 

č

estica fluida, 

kad stignu u tu to

č

ku, iste (konstantne, stalne, nepromjenljive, dakle, neovisne o vremenu) i jednake 

fizikalnim veli

č

inama prethodnih 

č

estica kad su bile u toj to

č

ki, a koje zamjenjuju u toj to

č

ki, strujanje je 

stacionarno (ustaljeno). 

(O tome je bilo govora u prvom udžbeniku.)

 Primjerice, brzina je svake 

č

estice fluida, 

kad stigne u to

č

ku A(x

A

,y

A

,z

A

), jednaka brzini 

A

c



č

estice koju zamjenjuje u toj to

č

ki. Dakle je: 





,

,

.

A

A

A

A

A

c

c

x

y

z

konst









Isto vrijedi za njihove akceleracije, temperaturu i tlak, kojima su izložene u toj to

č

ki, itd. Ustaljenost 

(stacionarnost) zna

č

i dakle nepromjenljivost u to

č

kama prostora kroz koje struji fluid: 

...

0

c

a

T

p

h

t

t

t

t

t

t

























 

















U suprotnom, strujanje je nestacionarno (neustaljeno). U tom slu

č

aju fizikalne se veli

č

ine 

č

estica 

pristiglih u to

č

ku A razlikuju od fizikalnih veli

č

ina 

č

estica koje zamjenjuju. Tada dakle vrijedi, za brzinu 

primjerice, 





,

,

,

.

A

A

A

A

A

c

c

x

y

z t

konst









Dakako, isto i za sve ostale fizikalne veli

č

ine. 

Promatranje je stacionarnih pojava jednostavnije, pa 

ć

emo, kad je to mogu

ć

e, nestacionarno strujanje 

„pretvarati“ u stacionarno. Primjerice, giba li se tijelo (torpedo) kroz fluid konstantnom brzinom, 

0

.,

c

konst





 slika 6.1, izborom mjesta opažanja, tj. koordinatnog sustava, mo

ć

i 

ć

emo nestacionarno 

strujanje fluida „pretvoriti“ u stacionarno. 
 

114

Ponovimo li snimanje više puta, dobit 

ć

emo seriju krivulja, nazvanih strujnicama, kojima su tangente ti 

mali vektori brzina, slika 6.4. 

Slika 6.4 Slika strujnica 

Strujnice su prema tome linije koje su u prostoru strujanja fluida tangencijalne na vektor trenuta

č

ne 

brzine 

č

estice fluida na promatranom mjestu, slika 6.5. 

Slika 6.5 Strujnica i vektor brzine 

Promatramo li put duljine 

dr

dxi

dyj

dzk















i brzinu u to

č

ki A (

dr



 je paralelan vektoru lokalne brzine) 

,

x

y

z

c

c i

c j

c k















dobivamo, iz sli

č

nosti trokuta, da je jednadžba strujnice u skalarnom obliku 

x

y

z

dr

dx

dy

dz

c

c

c

c







(6.1) 

 
Strujanje se fluida u osnovi svodi na ovo, slika 6.6. 

Slika 6.6 Formiranje strujnice 

115

Č

estica 

ć

e fluida A, nakon vremena 

∆

t

, do

ć

i u to

č

ku gdje je dotad bila 

č

estica B, kojoj je opet ustupila 

mjesto 

č

estica C itd. Dobiveni niz staza tvori isprekidanu liniju A-B-C …, koja prelazi u neprekidnu 

krivulju, strujnicu, kad skra

ć

ujemo vrijeme opažanja (

∆

t 

→

0)

. 

Brzina 

č

estice, npr. 

č

estice B, 

c

2

, 

usmjerena je veli

č

ina, vektor, kojem se smjer podudara s tangentom na strujnicu. Ako je strujanje 

nestacionarno, strujnica 

ć

e u prostoru mijenjati svoj oblik i položaj. 

Razliku izme

đ

u staze i strujnice razabrat 

ć

emo najo

č

itije promatraju

ć

i gibanje 

č

vrstog tijela kroz fluid, 

slika 6.7. 
 

Slika 6.7 Strujnice i staze nestacionarnog strujanja 

Č

vrsto 

ć

e tijelo, gibaju

ć

i se kroz fluid, gurati pred sobom 

č

estice fluida, a iza tijela 

č

estice 

ć

e nahrupiti u 

prazan prostor nastao pomakom tijela. Strujnice smo ozna

č

ili crticama budu

ć

i da su one putovi više 

č

estica promatranih istodobno. Slika 6.7a) je trenuta

č

na (momentalna) slika u prostoru fizi

č

ara A, pa su 

i strujnice trenuta

č

ne (momentalne), tj. one se u nekoj fiksnoj to

č

ki u koordinatnom sustavu fizi

č

ara A 

mijenjaju. Tako 

ć

e kroz to

č

ku T (s koordinatama x,y,z) prostora prolaziti momentalna strujnica I, a 

brzina 

ć

e 

c

1

 imati nazna

č

eni smjer. Nakon vremenskog intervala 

dt

 slika 

ć

e se pomaknuti ulijevo za 

dr

 pa 

ć

e kroz to

č

ku T prolaziti neka druga strujnica, npr. strujnica II, a brzina 

ć

e bit 

c

2

 itd. Osobito se jasno 

vidi razlika nakon daljnjeg (ve

ć

eg) vremenskog intervala, kada pro

đ

e ista (zapravo analogna) strujnica II 

kroz to

č

ku T: smjer 

c

2

'

 je bitno promijenjen. Ako bismo, me

đ

utim, slijedili jednu 

č

esticu, koja je u 

nekom trenutku bila npr. na strujnici II, ona bi u prostoru opisala put nacrtan na slici 6.7b). To je staza 

č

estice kako bi je snimio fizi

č

ar A.  

U stacionarnom se strujanju slika ne mijenja; staze se i strujnice podudaraju, one su identi

č

ne, slika 6.8. 

117

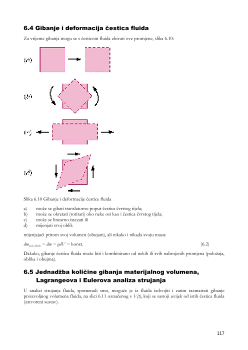
6.4 Gibanje i deformacija 

č

estica fluida 

Za vrijeme gibanja mogu se s 

č

esticom fluida zbivati ove promjene, slika 6.10: 

Slika 6.10 Gibanje i deformacije 

č

estice fluida 

a)

može se gibati translatorno poput 

č

estica 

č

vrstog tijela; 

b)

može se okretati (rotirati) oko neke osi kao i 

č

estica 

č

vrstog tijela; 

c)

može se linearno istezati ili  

d)

mijenjati svoj oblik 

mijenjaju

ć

i pritom svoj volumen (obujam), ali nikako i nikada svoju masu:  

dm

č

estice fluida

 = dm = 

ρ

dV =

 konst.  

(6.2) 

Dakako, gibanje 

č

estica fluida može biti i kombinirano od nekih ili svih nabrojenih promjena (položaja, 

oblika i obujma). 
 

6.5 Jednadžba koli

č

ine gibanja materijalnog volumena, 

Lagrangeova i Eulerova analiza strujanja 

U analizi strujanja fluida, spomenuli smo, mogu

ć

e je iz fluida izdvojiti i zatim razmatrati gibanje 

proizvoljnog volumena fluida, na slici 6.11 ozna

č

enog s 

V(t)

,

koji se sastoji uvijek od istih 

č

estica fluida 

(zatvoreni sustav).